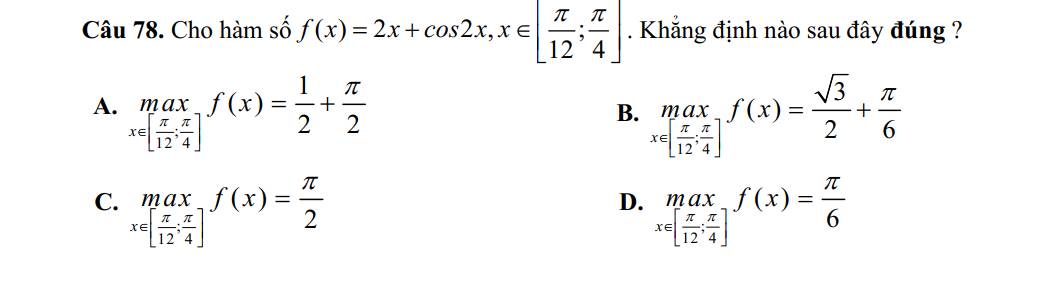- Cho 1 dãy các số nguyên (gồm cả các số âm và dương). Đặt vào giữa các số phép tính (+) hoặc (-) sao cho kết quả nhận được là nhỏ nhất và > = 0. Ví dụ, input là dãy số: 5, 1, -3, 9, 2 Thì output = (5 - 1 -(-3) - 9 + 2) = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

bạn xem lại sách nhé. tính f', tìm nghiệm f'=0, xét dấu f', xác định tính đơn điệu của hàm số, tìm các điểm cực trị. Vẽ đồ thị hàm số

hàm số đã cho xác định và liên tục trên đoạn \(\left[\dfrac{\pi}{12};\dfrac{\pi}{4}\right]\)
f'(x) = 2 - 2sin(2x) = 0 => sin(2x) = 1 => \(x=\dfrac{\pi}{4}\in\left[\dfrac{\pi}{12};\dfrac{\pi}{4}\right]\text{}\)
ta có: \(f\left(\dfrac{\pi}{12}\right)=\dfrac{\pi}{6}+\dfrac{\sqrt{3}}{2}< f\left(\dfrac{\pi}{4}\right)=\dfrac{\pi}{2}\)
vậy \(\max\limits_{x\in\left[\dfrac{\pi}{12};\dfrac{\pi}{4}\right]}y=f\left(\dfrac{\pi}{4}\right)=\dfrac{\pi}{2}\)
=> C

\(y'=x^2+2mx+2m-1\)
Hàm có cực trị khi \(\Delta'>0\)
\(\Rightarrow m^2-2m+1>0\)
\(\Rightarrow m\ne1\)

\(y=\dfrac{-x^2+mx-2}{x+1}\)
\(y'=\dfrac{\left(-2x+m\right)\left(x+1\right)-\left(-x^2+mx-2\right)}{\left(x+1\right)^2}=\dfrac{-x^2-2x+m+2}{\left(x+1\right)^2}\)
Hàm nghịch biến trên các khoảng xác định khi:
\(-x^2-2x+m+2\le0;\forall m\)
\(\Leftrightarrow\Delta'=1+\left(m+2\right)\le0\)
\(\Rightarrow m\le-3\)

\(y=\dfrac{2x+1}{x+3}\Rightarrow y'=\dfrac{5}{\left(x+3\right)^2}>0;\forall x\in TXĐ\)
\(y=-x^4+2x^2+1\Rightarrow y'=-4x^3+4x=0\Rightarrow x=\left\{-1;0;1\right\}\) có cực trị nên có các khoảng ĐB, NB (có thể nhớ nhanh là hàm bậc 4 ko bao giờ ĐB hoặc nghịch biến trên R)
\(y=3x^3+x-3\Rightarrow y'=9x^2+1>0;\forall x\)
Vậy (I) và (III) đồng biến trên các khoảng xác định
A đúng

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow\widehat{DSA}\) là góc giữa SD và (SAB)
\(\Rightarrow\widehat{DSA}=60^0\)
\(\Rightarrow SA=\dfrac{AD}{tan60^0}=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow V_{S.ABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{a^3\sqrt{3}}{18}\)
{SA⊥(ABCD)⇒SA⊥ADAD⊥AB \Rightarrow AD\perp\left(SAB\right)⇒AD⊥(SAB)
\Rightarrow\widehat{DSA}⇒DSA là góc giữa SD và (SAB)
\Rightarrow\widehat{DSA}=60^0⇒DSA=600
\Rightarrow SA=\dfrac{AD}{tan60^0}=\dfrac{a\sqrt{3}}{3}⇒SA=tan600AD=3a3
\Rightarrow V_{S.ABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.AC=\dfrac{a^3\sqrt{3}}{18}⇒VS.ABC=31SA.21AB.AC=18a33