Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K.
a) Chứng minh tứ giác AHCK là hình bình hành.
b) Gọi I là trung điểm của HK. Chứng minh IB = ID.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có : t/g ABCD là hbh
Suy ra : AD=BC
Mà E là trung điểm của AD ; F là trung điểm của BC
Suy ra : AE=DE=BF=CF
Xét tứ giác EBFD có : BF//ED ( BC//AD )
BF=ED ( cmt )
Suy ra : t/g EBFD là hbh.
b) Từ O là giao điểm của hai đường chéo của hbh ABCD hay là giao điểm của AC và BD.
Suy ra : O là trung điểm của BD hay 3 điểm B ; O ; D thẳng hàng
Ta có : t/g EBFD là hbh ( cmt )
Suy ra : BD cắt EF tại trung điểm của mỗi đường .
Mà O là trung điểm của BD
Suy ra : O cũng là trung điểm của EF.
suy ra : 3 điểm F;O;E thẳng hàng.
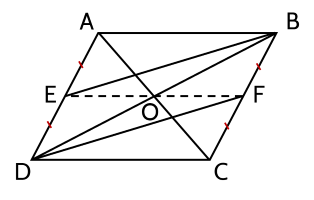
a) ABCD là hình bình hành nên AD = BC và AD // BC.
Mà E là trung điểm của AD nên AE = ED;
F là trung điểm của BC nên BF = FC.
Suy ra DE = BF.
Xét tứ giác EBFD có DE // BF (do AD // BC) và DE = BF nên là hình bình hành (dấu hiệu nhận biết).
b) Ta có O là giao điểm của hai đường chéo của hình bình hành ABCD nên O là trung điểm của BD.
Do EBFD là hình bình hành nên hai đường chéo BD và EF cắt nhau tại trung điểm của mỗi đường.
Mà O là trung điểm của BD nên O là trung điểm của EF.
Vậy ba điểm E, O, F thẳng hàng.

A B C G M N P Q
Xét tg ABG có
NA=NC; PB=PG => PN là đường trung bình của tg ABG
\(\Rightarrow PN=\dfrac{1}{2}AG\) (1)
=> PN//AG (2)
Xét tg ACG có
MA=MC; QC=QG => QN là đường trung bình của tg ACG
\(\Rightarrow QM=\dfrac{1}{2}AG\) (3)
=> QM//AG (4)
Từ (2) và (4) => PN//QM
Từ (1) và (3) \(\Rightarrow PN=QM=\dfrac{1}{2}AG\)
=> PQMN là hình bình hành (Tứ giác có một cặp cạnh đối // và = nhau là hbh)
Xét tg ABG có
NA=NC; PB=PG => PN là đường trung bình của tg ABG
⇒��=12��⇒PN=21AG (1)
=> PN//AG (2)
Xét tg ACG có
MA=MC; QC=QG => QN là đường trung bình của tg ACG
⇒��=12��⇒QM=21AG (3)
=> QM//AG (4)
Từ (2) và (4) => PN//QM
Từ (1) và (3) ⇒��=��=12��⇒PN=QM=21AG
=> PQMN là hình bình hành (Tứ giác có một cặp cạnh đối // và = nhau là hbh)

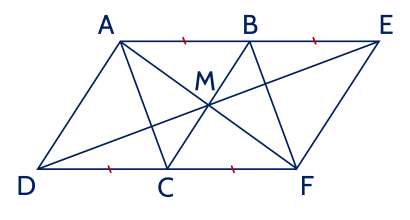
a) Vì ABCD là hình bình hành nên AB = CD; AB // CD.
Mà hai điểm B, C lần lượt là trung điểm AE, DF.
Suy ra AE = DF; AB = BE = CD = CF.
Tứ giác AEFD có AE // DF (vì AB // CD); AE = DF (chứng minh trên).
Do đó tứ giác AEFD là hình bình hành.
Tứ giác ABFC có AB // CF (vì AB // CD); AB = CF (chứng minh trên).
Do đó tứ giác ABFC là hình bình hành.
b) Vì hình bình hành AEFD có hai đường chéo AF và DE nên chúng cắt nhau tại trung điểm của mỗi đường, ta gọi giao điểm đó là O.
Hình bình hành AEFD có hai đường chéo AF và BC.
Mà O là trung điểm của AF.
Suy ra O cũng là trung điểm của BC.
Vậy các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.

A B C D O M N
Xét tg OAM và tg OCN có
\(\widehat{BAC}=\widehat{ACD}\) (góc so le trong)
OA=OC (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)
\(\widehat{AOM}=\widehat{CON}\) (góc đối đỉnh)
=> tg OAM = tg OCN (g.c.g) => AM=CN
Ta có
AB=CD (cạnh đối hbh) => AB-AM=CD-CN => MB=ND (1)
Ta có
AB//CD (cạnh đối hbh) => MB//ND (2)
Từ (1) và (2) => MBND là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)
Xét tg OAM và tg OCN có
���^=���^BAC=ACD (góc so le trong)
OA=OC (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)
���^=���^AOM=CON (góc đối đỉnh)
=> tg OAM = tg OCN (g.c.g) => AM=CN
Ta có
AB=CD (cạnh đối hbh) => AB-AM=CD-CN => MB=ND (1)
Ta có
AB//CD (cạnh đối hbh) => MB//ND (2)
Từ (1) và (2) => MBND là hình bình hành (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)

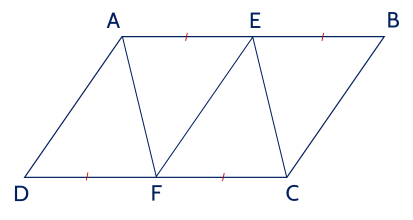
a) Vì ABCD là hình bình hành nên AB = CD, AB // CD.
Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE = 1221AB, CF = DF = 1221CD
Do đó AE = BE = CF = DF.
Xét tứ giác AEFD có:
AE // DF (vì AB // CD);
AE = DF (chứng minh trên)
Do đó tứ giác AEFD là hình bình hành.
Xét tứ giác AECF có:
AE // CF (vì AB // CD);
AE = CF (chứng minh trên)
Do đó tứ giác AECF là hình bình hành.
Vậy hai tứ giác AEFD, AECF là những hình bình hành.
b) Vì tứ giác AEFD là hình bình hành nên EF = AD.
Vì tứ giác AECF là hình bình hành nên AF = EC.
Vậy EF = AD, AF = EC.

1/
\(AH\perp BD;CK\perp BD\) (gt) => AH//CK (cùng vg với BD) (1)
Xét tg vuông ADH và tg vuông CBK có
AD=BC (cạnh đối hbh)
\(\widehat{ADH}=\widehat{CBK}\) (góc so le trong)
=> tg ADH = tg CBK (hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
=> AH=CK (2)
Từ (1) và (2) => AHCK là hbh (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)
2/
Nối AC cắt HK tai I' => I'H=I'K (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)
Mà IH=IK (gt)
=> \(I\equiv I'\) => A; I; C thẳng hàng

\(\left(x-1\right)\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1\text{=}0\\x^2-3x+2\text{=}0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\text{=}1\\x^2-3x+2\text{=}0\left(1\right)\end{matrix}\right.\)
Giải pt (1) ta có :
\(\left(1\right)\Leftrightarrow x^2-x-2x+2\text{=}0\)
\(\Leftrightarrow x\left(x-1\right)-2\left(x-1\right)\text{=}0\)
\(\Leftrightarrow\left(x-2\right)\left(x-1\right)\text{=}0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2\text{=}0\\x-1\text{=}0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\text{=}2\\x\text{=}1\end{matrix}\right.\)
Vậy.....

a) Ta có : t/g ABCD là hbh
Suy ra : AB//CD
Suy ra : góc FAE = góc AED ( 2 góc ở vị trí slt)
Mà góc FAE = góc DAE ( AE là tia p/g của góc A )
Suy ra : góc DAE = góc DEA
Suy ra : tam giác ADE cân tại D
b) CMTT : tam giác FBC cân tại B ( như phần a )
Suy ra : BC = BF
c) Từ (a) suy ra : AD=DE ( tam giác ADE cân tại D )
Mà BC=BF ( theo b )
Suy ra : BF=BC=AD=DE
Suy ra : DE=BF
d) Từ c) suy ra : DE=BF
Ta có : AB = AF+FB
CD=DE+CE
Mà : DE=BF ; AB=CD ( ABCD là hbh )
Suy ra : AF=CE
Xét t/g AECF có : AF//CE ( AB//CD)
AF=CE ( cmt )
Suy ra : t/g AECF là hbh.

a,
A = 20182 - 20172
A = (2018 - 2017).(2018 + 2017) = 2018 + 2017
B = (20172 - 20162)
B = (2017 - 2016).(2017 + 2016) = 2016 + 2017
Vì 2018 + 2017 > 2016 + 2017 nên A > B
b, C = 20182 + 20162; D = 2.20172
C = 20182 + 20162 - 2.20172
C - D = (20182 - 20172) - (20172 - 20162)
C - D = A - B > 0
⇒ C > D
a) Do ABCD là hình bình hành
\(\Rightarrow AD=BC\) và \(AD\) // \(BC\)
Do \(AD\) // \(BC\) (cmt)
\(\Rightarrow\widehat{ADH}=\widehat{CBK}\) (so le trong)
Xét hai tam giác vuông: \(\Delta ADH\) và \(\Delta CBK\) có:
\(AD=BC\) (cmt)
\(\widehat{ADH}=\widehat{CBK}\) (cmt)
\(\Rightarrow\Delta ADH=\Delta CBK\) (cạnh huyền - góc nhọn)
\(\Rightarrow AH=CK\) (hai cạnh tương ứng)
Do \(AH\perp BD\) (gt)
\(CK\perp BD\) (gt)
\(\Rightarrow AH\) // \(CK\)
Xét tứ giác AHCK có:
\(AH\) // \(CK\) (cmt)
\(AH=CK\) (cmt)
\(\Rightarrow AHCK\) là hình bình hành
b) Do AHCK là hình bình hành (cmt)
\(I\) là trung điểm của HK (gt)
\(\Rightarrow I\) là trung điểm của AC
Do ABCD là hình bình hành (gt)
\(I\) là trung điểm của AC (cmt)
\(\Rightarrow I\) là trung điểm của BD
\(\Rightarrow IB=ID\)
a) Xét : \(\Delta ADHvà\Delta CBK\) có :
góc : AHD = góc : CKB ( = 90 độ )
AD=BC ( ABCD là hbh )
góc ADH = góc CBK ( 2 góc ở vị trí slt tạo bởi 2 đường thẳng song song là AD và BC )
Do đó : \(\Delta ADH\text{=}\Delta CBK\left(c.h-g.n\right)\)
\(\Rightarrow AH\text{=}CK\)
Xét t/g AHCK có : AH//CK ( cùng vuông góc với BD )
AH = CK (cmt)
Suy ra : t/g AHCK là hbh.
b) Từ a) : suy ra : AHCK là hbh.
Suy ra : AC cắt HK tại trung điểm của mỗi đường.
Mà I là trung điểm của HK.
Suy ra : I cũng là trung điểm của AC.
Ta có : ABCD là hbh.
Suy ra : AC cắt BD tại trung điểm của mỗi đường .
Mà I là trung điểm của AC.
Suy ra : I cũng là trung điểm của BD.
Suy ra : IB=ID.