1 quầy bán hàng có 93kg gồm loại 1kg, loại 0,5kg và loại 0,2kg. Khối lượng cả 93 gói là 43,4kg. Hỏi mỗi loại có bao nhiêu gói. Biết số gói 0,5kg gấp rưỡi số gói 0,2kg
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khi sắp phép tính thẳng hàng bên trái thì số hạng thứ hai tăng gấp 10 lần
Số lần số hạng thứ hai tăng thêm:
10 - 1 = 9 (lần)
Số hạng thứ hai là:
4824 : 9 = 536
Kết quả đúng của phép tính:
6354 + 536 = 6890

\(x+\left(\dfrac{2}{5}\right)^2=\dfrac{9}{10}\)
=>\(x+\dfrac{4}{25}=\dfrac{9}{10}\)
=>\(x=\dfrac{9}{10}-\dfrac{4}{25}=\dfrac{45}{50}-\dfrac{8}{50}=\dfrac{37}{50}\)
`x + (2/5)^2 = 9/10`
`=> x + 4/25 = 9/10`
`=> x = 9/10 - 4/25`
`=> x = 45/50 - 8/50`
`=> x = 37/50`
-------------------------
`(x+2/5)^2 = 9/10`
`=> (x+2/5)^2 = (3/sqrt{10})^2`
`=> x + 2/5 = 3/sqrt{10}` hoặc `x + 2/5 = -3/sqrt{10}`
`=> x = 3/sqrt{10} - 2/5` hoặc `x = -3/sqrt{10} - 2/5`
`=> x = (-4+3sqrt{10})/10` hoặc `x = -(4+3sqrt{10})/10`

Số quả trứng bán đi trong lần đầu là:
`336 xx 5 : 12 = 140` (quả trứng)
Số quả trứng còn lại sau lần đầu bán đi là;
`336 - 140 = 196` (quả trứng)
Số quả trứng bán đi trong lân thứ 2 là:
` 196 : 4 xx 3 = 147` (quả trứng)
Lần 3 bán số quả trứng là:
`196 - 147 = 49` (quả trứng)
Đáp số: `49` quả trứng
Sau lần đầu thì số quả trứng còn lại là:
\(336\times\left(1-\dfrac{5}{12}\right)=336\times\dfrac{7}{12}=196\left(quả\right)\)
Số quả trứng lần thứ ba bán được là:
\(196\times\left(1-\dfrac{3}{4}\right)=49\left(quả\right)\)

a: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(C=\left(\dfrac{1}{x^2+1}-\dfrac{x+1}{x^4-1}\right):\dfrac{x+1}{x^5+x^4-x-1}\)
\(=\dfrac{x^2-1-x-1}{\left(x^2+1\right)\left(x^2-1\right)}:\dfrac{x+1}{x^4\left(x+1\right)-\left(x+1\right)}\)
\(=\dfrac{x^2-x-2}{\left(x^2+1\right)\left(x-1\right)\left(x+1\right)}\cdot\dfrac{\left(x+1\right)\left(x^4-1\right)}{x+1}\)
\(=\dfrac{\left(x-2\right)\left(x+1\right)}{\left(x^2+1\right)\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x^4-1}{1}\)
=(x-2)(x+1)
b: Để C=0 thì (x-2)(x+1)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
c: \(C=\left(x-2\right)\left(x+1\right)=x^2-x-2\)
\(=x^2-x+\dfrac{1}{4}-\dfrac{9}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2-\dfrac{9}{4}>=-\dfrac{9}{4}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{2}=0\)
=>\(x=\dfrac{1}{2}\)

Vì số sách toán 5 là trung bình cộng của số sách Toán 4 và Toán 3 nên số sách toán 3 và 4 gấp 2 lần số sách toán 5
Hay Số sách toán 5 bằng `1/3` tổng số sách bán đi
Số sách toán 5 bán được là :
`45:3= 15` (sách)
Tổng số sách toán 3 và 4 là :
`45 - 15 = 30` (sách)
Số tiền có được từ 15 sách toán 5 là :
`15xx 6000= 90 000` (đồng. )
Tổng số tiền mua sách toán 3 và 4 là:
`230 000- 90 000= 140 000` (đồng. )
Giả sử mỗi cuốn sách toán 4 cũng là 4000 đồng thì tổng số tiền bán sách toán 3 và 4 là:
`4000xx30 = 120000` (đồng. )
Số tiền giảm đi so với thực tế là;
`140000-120000= 20000` (đồng. )
Hiệu giá tiền của sách toán 4 và 3 là:
`5000 - 4000 = 1000` (đồng)
Số sách toán 4 bán được là:
`20000:1000= 20` (sách)
Số sách toán 3 bán được là:
`30-20 =10` (sách)
Đáp số: ...

3a=5b
=>\(a=\dfrac{5b}{3}\)
a-b=-6
=>\(\dfrac{5b}{3}-b=-6\)
=>\(\dfrac{2}{3}b=-6\)
=>\(b=-6:\dfrac{2}{3}=-6\cdot\dfrac{3}{2}=-9\)
=>\(b=\dfrac{5}{3}\cdot\left(-9\right)=-15\)

a: Vì ABCD là hình thang
nên \(\dfrac{S_{ABC}}{S_{ACD}}=\dfrac{AB}{CD}=\dfrac{2}{3}\)
b: Diện tích hình thang ABCD là:
\(S_{ABCD}=\dfrac{1}{2}\cdot3\cdot\left(2+3\right)=\dfrac{15}{2}\left(cm^2\right)\)
\(\dfrac{S_{ABC}}{S_{ADC}}=\dfrac{2}{3}\)
=>\(S_{ADC}=1,5\cdot S_{ABC}\)
\(S_{ABC}+S_{ADC}=S_{ABCD}\)
=>\(1,5\cdot S_{ABC}+S_{ABC}=7,5\)
=>\(2,5\cdot S_{ABC}=7,5\)
=>\(S_{ABC}=3\left(cm^2\right)\)

a,b,c là các số thực đôi một phân biệt
=>\(a-b;b-c;a-c\) đều khác 0
\(a^3+b^3+c^3=3bac\)
=>\(\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
=>\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)=0\)
=>\(\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\)
=>\(\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)
=>\(\left(a+b+c\right)\left[2a^2+2b^2+2c^2-2ab-2ac-2bc\right]=0\)
=>\(\left(a+b+c\right)\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\right]=0\)
=>\(\left[{}\begin{matrix}a+b+c=0\\\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a+b+c=0\\a=b=c\left(loại\right)\end{matrix}\right.\)
=>a+b+c=0
=>a+b=-c; a+c=-b; b+c=-a
\(P=\dfrac{a+b}{c}\cdot\dfrac{b+c}{a}\cdot\dfrac{c+a}{b}=\dfrac{-c}{c}\cdot\dfrac{-a}{a}\cdot\dfrac{-b}{b}=-1\)

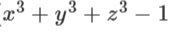
Giả sử cả 48 gói kẹo đều là loại 0,5 kg thì khối lượng cả 48 gói kẹo sẽ là:
0,5 x 48 = 24 (kg)
Số kg kẹo dôi ra là
24 – 9 = 15 (kg)
Số kẹo dôi ra vì ta đã thay gói 0,2 kg và gói 0,1 kg bằng gói 0,5 kg.
Số gói 0,1 kg gấp 3 lần số gói 0,2 kg nên mỗi lần thay 1 gói 0,2 kg và 3 gói 0,1 kg bằng 4 gói 0,5 kg thì khối lượng kẹo tăng:
0,5 x 4 – 0,2 x 1 – 0,1 x 3 = 1,5 (kg)
Số lần thay là:
15 : 1,5 = 10 (lần)
Vậy số gói kẹo 0,2 kg là 10 gói
Số gói kẹo loại 0,1 kg là
10 x 3 = 30 (kg)
Số gói kẹo loại 0,5 kg là
48 – 30 – 10 = 8 (gói)
Đáp số: Số gói loại 0,2 kg: 10 gói
Số gói loại 0,1 kg: 30 gói
Số gói loại 0,5 kg: 8 gói