Gọi giá tiền mua 1 kg táo, 1kg bưởi và 1 kg dưa hấu lần lượt là a(đồng),b(đồng),c(đồng)

Vì số tiền để cô Mai mua táo  bằng số tiền mua bưởi và dưa hấu nên 3a=6b=10c

=>\(\dfrac{3a}{30}=\dfrac{6b}{30}=\dfrac{10c}{30}\)

=>\(\dfrac{a}{10}=\dfrac{b}{5}=\dfrac{c}{3}\)

Giá 1kg bưởi hơn 1kg dưa hấu 18000 đồng nên b-c=18000

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{10}=\dfrac{b}{5}=\dfrac{c}{3}=\dfrac{b-c}{5-3}=\dfrac{18000}{2}=9000\)

=>\(a=9000\cdot10=90000;b=9000\cdot5=45000;c=9000\cdot3=27000\)

Vậy: giá tiền mua 1 kg táo, 1kg bưởi và 1 kg dưa hấu lần lượt là 90000 đồng; 45000 đồng; 27000 đồng

a: Xét ΔABC có AB<AC

mà \(\widehat{ACB};\widehat{ABC}\) lần lượt là góc đối diện của cạnh AB,AC

nên \(\widehat{ACB}< \widehat{ABC}\)

V

nham̀ a_a

Các nhận xét đúng là nhận xét 1;2

a: Sửa đề: ΔBAD=ΔBED

Xét ΔBAD và ΔBED có

BA=BE

\(\widehat{ABD}=\widehat{EBD}\)

BD chung

Do đó: ΔBAD=ΔBED

b: Xét ΔMDH và ΔMCB có

\(\widehat{MDH}=\widehat{MCB}\)(hai góc so le trong, DH//BC)

MD=MC

\(\widehat{DMH}=\widehat{CMB}\)(hai góc đối đỉnh)

Do đó: ΔMDH=ΔMCB

=>DH=CB

Câu 27:

a: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có

CA chung

AB=AD

Do đó: ΔCAB=ΔCAD

=>CB=CD

=>ΔDBC cân tại C

b: Xét ΔMCB và ΔMDE có

\(\widehat{MCB}=\widehat{MDE}\)(hai góc so le trong, BC//DE)

MC=MD

\(\widehat{CMB}=\widehat{DME}\)(hai góc đối đỉnh)

Do đó: ΔMCB=ΔMDE

=>BC=DE

Xét ΔEDB có ED+DB>BE

mà ED=BC

nên BD+BC>BE

Câu 26:

a: Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)

Xét ΔABC có AB<AC<BC

mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC

nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)

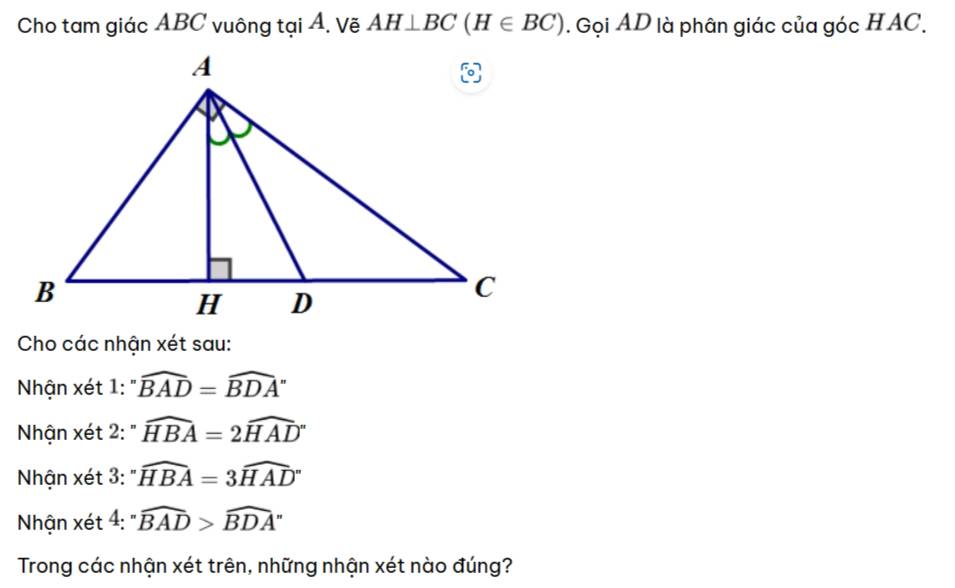
b: xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

BD chung

Do đó: ΔBAD=ΔBED

=>DA=DE

c: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có

DA=DE

\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)

Do đó: ΔDAF=ΔDEC

=>DF=DC

mà DC>DE(ΔDEC vuông tại E)

nên DF>DE

a)Ta có tam giác ABC cân

=>:AB=AC;góc B=góc C.

Xét tam giác AMB và tam giác AMC có:

AB=AC(cmt)

góc BAM=góc CAM (AM là phân giác của góc A).

AM chung.

=>tam giác AMB = tam giác AMC(c-g-c)

b) Vì tam giác AMB = tam giác AMC

=>góc AMB=góc AMC (2 góc tương ứng)

Mà 2 góc ở vị trí kề bù => góc AMB=góc AMC=180:2=90độ

=>AM vuông góc BC

c)

Nếu M là điểm tùy ý trên AH thì BM = MC chứ không phải BM = BA em nhé. 

@Nguyễn Thị Thương Hoài :vâng

Em cần viết đề bài bằng công thức toán học với biểu tượng Σ trên góc trái màn hình thì mọi người mới hiểu đúng đề để giúp em được.

                   2\(x\) = 3y ⇒  \(x\) = \(\dfrac{3}{2}\)y

                    4y = 5z ⇒ z = \(\dfrac{4}{5}y\)

               Thay \(x=\dfrac{3}{2}y;\)  z = \(\dfrac{4}{5}y\)  vào \(x+y+z\) = 11 ta có:

                        \(\dfrac{3}{2}y\) + y + \(\dfrac{4}{5}y\) = 11

                           \(\dfrac{33}{10}\)y           = 11

                               y            = 11 : \(\dfrac{33}{10}\)

                              y             = \(\dfrac{10}{3}\)

                               \(x\) = \(\dfrac{3}{2}\) x \(\dfrac{10}{3}\) = 5

                               z = \(\dfrac{4}{5}\) x \(\dfrac{10}{3}\) = \(\dfrac{8}{3}\)

Vậy \(\left(x;y;z\right)\) = (5; \(\dfrac{10}{3}\); \(\dfrac{8}{3}\))