Giải tam giác ABC, biết BC = 12 m, AC = 31 m và A = 20,5°
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`->` Chưa đúng.
`-` Xét:
`+` Hai cặp cạnh đối song song.
`+` Hai cặp cạnh đối bằng nhau.
`+` Hai cặp góc đối bằng nhau.
`+` Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
`+` Một cặp cạnh đối vừa song song vừa bằng nhau.

\(sina=\dfrac{2}{3}\left(0< a< 90^o\right)\)
\(sin^2a+cos^2b=1\Rightarrow cos^2a=1-sin^2a=1-\dfrac{4}{9}=\dfrac{5}{9}\)
\(\Rightarrow cosa=\dfrac{\sqrt{5}}{3}\left(0< a< 90^o\Rightarrow cosa>0\right)\)
\(tana=\dfrac{sina}{cosa}=\dfrac{\dfrac{2}{3}}{\dfrac{\sqrt{5}}{3}}=\dfrac{2}{\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
\(P=tana-3cosa=\dfrac{2\sqrt{5}}{5}-3.\dfrac{\sqrt{5}}{3}=\dfrac{2\sqrt{5}}{5}-\sqrt{5}=\dfrac{-3\sqrt{5}}{5}\)

Bài 2:
a) Mệnh đề phủ định là: \("\exists x\in R;n⋮̸n"\)
Mà `n⋮n` với mọi n => Mệnh đề sai
b) Mệnh đề phủ định là: \("\forall x\in Q;x^2\ne2"\)
Ta có: \(x^2\ne2\Leftrightarrow x\ne\pm\sqrt{2}\)
Mà: \(\pm\sqrt{2}\notin Q\) => Mệnh đề đúng
c) Mệnh đề phủ định là: \("\exists x\in R;x\ge x+1"\)
Mà: `x<x+1` với mọi x
`=>` Mệnh đề sai
d) Mệnh đề phủ định là \("\forall x\in R;3x=x^2+1"\)
Ta có: `3x=x^2+1`
`<=>x^2-3x+1=0`
\(\Delta=\left(-3\right)^2-4\cdot1\cdot1=5>0=>\left[{}\begin{matrix}x=\dfrac{3-\sqrt{5}}{2}\\x=\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\)
=> `3x=x^2+1` chỉ đúng với 2 giá trị
=> Mệnh đề sai
Bài 1: "\(\forall x\in R;\exists y\in R;y=x+3\)"
=>Mệnh đề này đúng vì với mọi giá trị của x luôn tồn tại một giá trị của y sao cho y=x+3
Mệnh đề phủ định là: "\(\exists x\in R;\forall y\in R;y\ne x+3\)"

Nếu \(a\ne3\Rightarrow\) tập B có phần tử 3 nhưng tập A ko có \(\Rightarrow A\ne B\) (ko thỏa mãn)
\(\Rightarrow a=3\)
Khi đó \(A=\left\{5;1;3\right\}\) ; \(B=\left\{5;3;b\right\}\)
\(\Rightarrow b=1\)

\(\Leftrightarrow2mx^2-2mx-x^2+1=0\)
\(\Leftrightarrow2mx\left(x-1\right)-\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2mx-x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\\left(2m-1\right)x=1\end{matrix}\right.\)
Pt có nghiệm thuộc khoảng đã cho khi \(\left(2m-1\right)x=1\) có nghiệm thuộc (-1;0)
\(\Rightarrow\left\{{}\begin{matrix}2m-1\ne0\\x=\dfrac{1}{2m-1}\in\left(-1;0\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\-1< \dfrac{1}{2m-1}< 0\end{matrix}\right.\) \(\Rightarrow m< 0\)

\(0< 25^0< 90^0\Rightarrow cos25^0>0\)
\(\Rightarrow cos25^0=\sqrt{1-sin^225^0}=\sqrt{1-a^2}\)
\(tan25^0=\dfrac{sin25^0}{cos25^0}=\dfrac{a}{\sqrt{1-a^2}}\)
\(cot25^0=\dfrac{1}{tan25^0}=\dfrac{\sqrt{1-a^2}}{a}\)

\(x^2-2x+m=0\Leftrightarrow x^2-2x-3=-m-3\)
Từ đồ thị ta thấy:
a.
Phương trình vô nghiệm khi \(-m-3< -4\Rightarrow m>1\)
b.
Phương trình có nghiệm kép khi \(-m-3=-4\Rightarrow m=1\)
c.
Phương trình có 2 nghiệm pb khi:
\(-m-3>-4\Rightarrow m< 1\)
d.
Phương trình có 2 nghiệm pb thuộc \(\left[-1;3\right]\) khi: \(-4< m\le0\)
e.
Có 2 nghiệm pb ko thuộc \(\left[-1;3\right]\) khi \(m>0\)


4d.
Để ý rằng tập \(3k+1\), nếu k lẻ hay \(k=2n+1\Rightarrow3k+1=3\left(2n+1\right)+1=6n+4\) chính là tập B
Nếu k chẵn hay \(k=2n\Rightarrow3k+1=6n+1\)
Từ đó ta có \(B\subset A\) nên:
\(A\cap B=B\)
\(A\cup B=A\)
\(A\backslash B=C\) với \(C=\left\{6n+1|n\in Z\right\}\)
\(B\backslash A=\varnothing\)
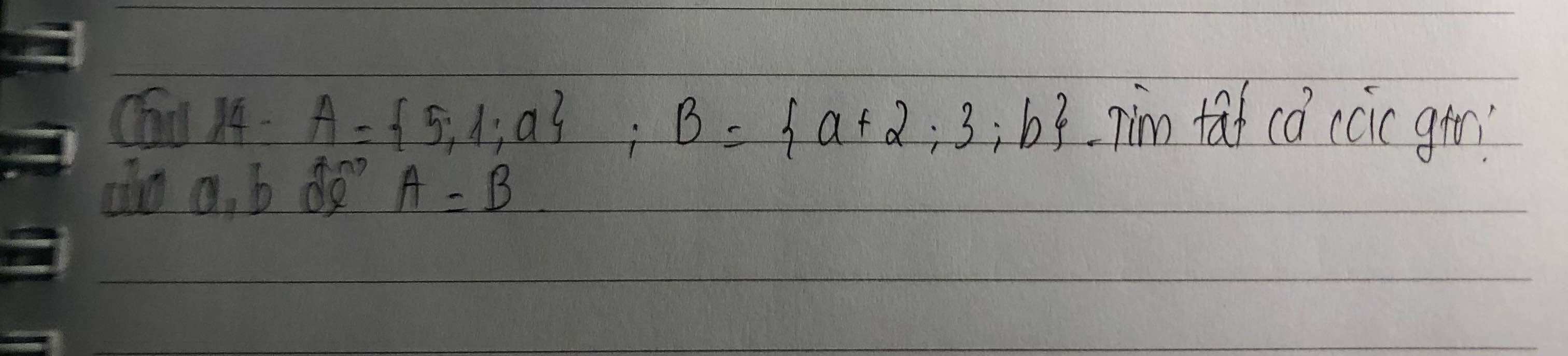


Đề ko đúng rồi em, dữ kiện cuối là góc thì phải có 3 điểm chứ