(x+5)(2-x)=\(3\sqrt{x^2+3x}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





e biết vẽ đồ thị của hàm \(\left(x-3\right)\left|x-1\right|\)dựa theo hàm số \(\left(x-3\right)\left(x-1\right)\)chưa nhỉ

do phương trình có hai nghiệm phân biệt nên \(\Delta=b^2-4c>0\Leftrightarrow b^2>4c\)
câu a. do tích hai nghiệm theo công thức vi-et là : \(x_1.x_2=c>1\)\(\Rightarrow b^2>4c>4\Rightarrow\)dpcm
bdo phương trình có hai nghiệm dương nên b<0 kết hợp đk của câu a ta có \(b\le-2\)
.\(P=\frac{3b^2-4c+b+2}{b^2+1}\ge\frac{3b^2-b^2+b+2}{b^2+1}=\frac{2b^2+b+2}{b^2+1}\)
\(\Rightarrow P\ge2+\frac{b}{b^2+1}=2-\frac{2}{5}+\frac{b}{b^2+1}+\frac{2}{5}=\frac{8}{5}+\frac{2b^2+5b+2}{5\left(b^2+1\right)}\)
\(=\frac{8}{5}+\frac{\left(2b+1\right)\left(b+2\right)}{5.\left(b^2+1\right)}\ge\frac{8}{5}\)( do \(b\le-2\Rightarrow\left(2b+1\right)\left(b+2\right)\ge0\)
Vậy GTNN của P= 8/5
dấu bằng khi b=-2
(x+5)(2-x)=3\(\sqrt{x^2+3x}\)
<=> -x2-3x+10= 3\(\sqrt{x^2+3x}\)
⇔ x2 + 3x + 3√(x2 + 3x) - 10 = 0
Đặt t = √(x2 + 3x), t ≥ 0. Phương trình đã cho trở thành
t2 + 3t - 10 = 0 ⇔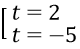
Vì t ≥ 0 ⇒ t = 2, thay vào ta có √(x2 + 3x) = 2
⇔ x2 + 3x - 4 = 0 ⇔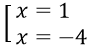
Vậy phương trình có nghiệm là x = 1 và x = -4