lẹ với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C M N
Ta có
\(BC=4CM\Rightarrow\dfrac{CM}{BC}=\dfrac{1}{4}\Rightarrow\dfrac{CM}{BM}=\dfrac{1}{3}=\dfrac{CN}{AN}\)
=> MN//AB (Talet đảo trong tam giác)

Lời giải:
Theo bài ra ta có:
$4x-12=2x+5+21$
$\Leftrightarrow 4x-12=2x+26$
$\Leftrightarrow 2x=38$
$\Leftrightarrow x=19$ (m)
Chiều dài là: $4.19-12=64$ (m)
Chiều rộng là: $2.19+5=43$ (m)
Chu vi mảnh vườn: $2(64+43)=214$ (m)

Lời giải:
Gọi $T$ là giao điểm $AK, DE$.
Xét tứ giác $ADHE$ có $\widehat{A}=\widehat{D}=\widehat{E}=90^0$ nên $ADHE$ là hình chữ nhật.
$\widehat{ADT}=\widehat{ADE}=\widehat{AHE}=90^0-\widehat{EHC}=\widehat{C}(1)$
Mặt khác:
Tam giác $ABC$ vuông tại $A$, $AK$ là đường trung tuyến ứng với cạnh huyền nên $AK=\frac{BC}{2}=BK$
$\Rightarrow ABK$ là tam giác cân tại $K$
$\Rightarrow \widehat{TAD}=\widehat{KAB}=\widehat{KBA}=\widehat{B}(2)$
Từ $(1); (2)\Rightarrow \widehat{ADT}+\widehat{TAD}=\widehat{B}+\widehat{C}=90^0$
$\Rightarrow \widehat{DTA}=180^0-(\widehat{ADT}+\widehat{TAD})=180^0-90^0=90^0$
$\Rightarrow DE\perp AK$ (đpcm)

Hiệu số phần bằng nhau là
4 - 3 = 1 ( phần )
Chiều dài khu đất là
50 : 1 x 4 = 200 ( m )
Chiều rộng khu đất là
200 - 50 = 150 ( m )
Diện tích khu đất là
200 x 150 = 30 000 ( m2 ) = 3 ha
ĐS :
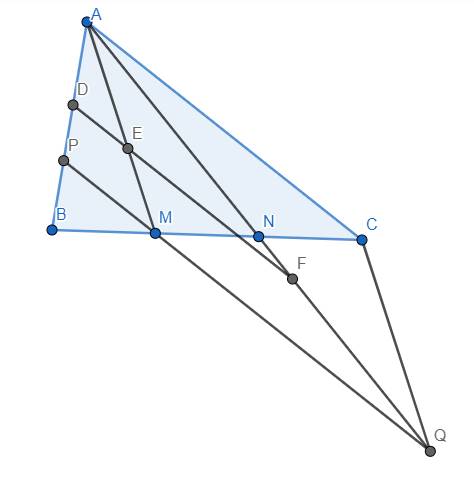
Qua M kẻ đường thẳng song song với AC cắt AB, AN lần lượt tại P và Q.
Ta thấy \(\widehat{ANC}=\widehat{QNM}\) (2 góc đối đỉnh), \(NM=NC\) (gt), \(\widehat{NCA}=\widehat{NMQ}\) (do AC//MQ) nên \(\Delta NAC=\Delta NQM\left(g.c.g\right)\)
\(\Rightarrow AC=MQ\)
Áp dụng định lý Thales trong tam giác ABC, ta có: \(\dfrac{BM}{BC}=\dfrac{PM}{AC}=\dfrac{PM}{MQ}\) \(\Rightarrow\dfrac{PM}{MQ}=\dfrac{1}{3}\)
Lại theo định lý Thales, trong tam giác APM, có: \(\dfrac{DE}{PM}=\dfrac{AE}{AM}\), trong tam giác AMQ, có \(\dfrac{AE}{AM}=\dfrac{EF}{MQ}\).
Từ đó, ta có \(\dfrac{DE}{PM}=\dfrac{EF}{MQ}\) \(\Rightarrow\dfrac{DE}{EF}=\dfrac{PM}{MQ}\). Mà \(\dfrac{PM}{MQ}=\dfrac{1}{3}\left(cmt\right)\) nên \(\dfrac{DE}{EF}=\dfrac{1}{3}\), hay \(EF=3DE\) (đpcm)

Bạn cần làm gì và điều kiện về $x,y$ như thế nào bạn nên ghi chú đầy đủ ra để mọi người trợ giúp tốt hơn.

bạn vào toán bình thường r kéo xuống khi đến bài đầu tiên của kì 2

Lời giải:
$ab+bc+ac=3abc\Rightarrow \frac{1}{a}+\frac{1}{b}+\frac{1}{c}=3$
Đặt $\frac{1}{a}=x, \frac{1}{b}=y; \frac{1}{c}=z$ thì bài toán trở thành:
Cho $x,y,z>0$ thỏa mãn $x+y+z=3$.
Tìm min $S=\sum \frac{x^3}{x^2+y^2}$
---------------------------
Có:
$S=\sum (x-\frac{xy^2}{x^2+y^2})=\sum x- \sum \frac{xy^2}{x^2+y^2}$
$=3-\sum \frac{xy^2}{x^2+y^2}$
$\geq 3-\sum \frac{xy^2}{2xy}=3-\sum \frac{y}{2}$ (áp dụng BĐT AM-GM)
$=3-\frac{3}{2}=\frac{3}{2}$
Vậy $S_{\min}=\frac{3}{2}$. Giá trị này đạt tại $x=y=z=1$ hay $a=b=c=1$
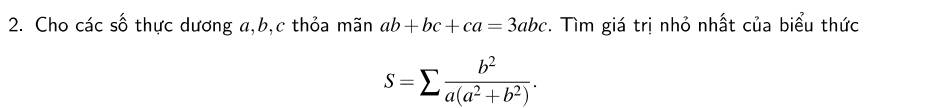
a, (a2 + b2).(c2 + d2)
= a2.c2 + a2.d2 + b2.c2 + b2.d2 (1)
(ac + bd)2 + (ad - bc)2
= a2.c2 + 2abcd + b2.d2 + a2.d2 - 2abcd + b2.c2
= a2.c2 + b2.d2 + a2.d2 + b2.c2 (2)
Kết hợp (1) và (2) ta có:
(a2+b2).(c2+d2) = (ac + bd)2 + (ad - bc)2 (đpcm)
Bài 4 ý 2,
(a + b + c)3
= (a+b)3 + 3(a+b)2.c + 3.(a+b).c2 + c3
= a3 + 3a2b+3ab2 + b3 + 3.(a+b).[ (a + b).c + c2] + c3
= a3 + 3a2b + 3ab2 + b3 + 3(a+b)[ac + bc + c2] + c3
= a3+b3+ c3 + 3ab.(a + b) + 3.(a + b)[ac + bc + c2]
= a3 + b3 + c3 + 3.(a + b).(ab + ac + bc + c2]
= a3 + b3 + c3 + 3.(a + b).[(ab + bc) + (ac + c2)]
= a3 + b3 + c3 + 3.(a + b).[b.(a + c) + c.(a + c)]
= a3 + b3 + c3 + 3.(a + b).(a+c).(b+c) (đpcm)