tìm x: \(\sqrt{x+3}\)+\(\sqrt{9x+27}\)-\(\sqrt{4x+12}\)=10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{x+2}\) + \(\sqrt{16x+32}\) - \(\sqrt{4x+8}\) = 16 (đk \(x\ge\) -2)
\(\sqrt{x+2}\) + \(\sqrt{16\left(x+2\right)}\) - \(\sqrt{4\left(x+2\right)}\) = 16
\(\sqrt{x+2}\) + 4\(\sqrt{x+2}\) - 2\(\sqrt{x+2}\) = 16
( 1 + 4 - 2)\(\sqrt{x+2}\) = 16
3\(\sqrt{x+2}\) = 16
\(\sqrt{x+2}\) = \(\dfrac{16}{3}\)
\(x+2\) = \(\dfrac{256}{9}\)
\(x\) = \(\dfrac{256}{9}\) - 2
\(x\) = \(\dfrac{238}{9}\) (thỏa mãn)
Vậy \(x=\dfrac{238}{9}\)

Ta thấy \(A-4=\dfrac{x+2\sqrt{x}+1}{\sqrt{x}}-4\)
\(=\dfrac{x+2\sqrt{x}+1-4\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{x-2\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}\)
Do \(\left(\sqrt{x}-1\right)^2\ge0\) và \(\sqrt{x}>0\) nên \(\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}\ge0\). ĐTXR \(\Leftrightarrow x=1\).
Như vậy \(A-4\ge0\) \(\Leftrightarrow A\ge4\)
(không phải là \(A>4\) như trong đề đâu nhé, dấu "=" vẫn có thể xảy ra nếu \(x=1\))

A B C H M N
a/
Xét tg vuông ABH
\(AH^2=AM.AB\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
Xét tg vuông ACH có
\(AH^2=AN.AC\) (lý do như trên)
\(\Rightarrow AM.AB=AN.AC\)
b/
\(AN\perp AB;MH\perp AB\) => AN//MH
\(AM\perp AC;NH\perp AC\) => AM//NH
=> AMHN là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một)
Mặt khác \(\widehat{A}=90^o\)
=> AMHN là HCN => AM=NH; AN=MH (cạnh đối HCN)
Xét tg vuông ABH và tg vuông ACH có
\(\widehat{BAH}=\widehat{ACB}\) (cùng phụ với \(\widehat{ABC}\) )
=> tg ABH đồng dạng với tg ACH
\(\Rightarrow\left(\dfrac{AB}{AC}\right)^2=\dfrac{S_{ABH}}{S_{ACH}}\) (hai tg đồng dạng, tỷ số 2 diện tích bằng bình phương tỷ số đồng dạng)
\(\Rightarrow\left(\dfrac{AB}{AC}\right)^2=\dfrac{\dfrac{1}{2}.AB.MH}{\dfrac{1}{2}.AC.NH}\Rightarrow\dfrac{AB}{AC}=\dfrac{MH}{NH}\) lập phương 2 vế
\(\dfrac{AB^3}{AC^3}=\dfrac{MH^2.MH}{NH^2.NH}\) (1)
Xét tg vuông ABH
\(MH^2=BM.AM\) (trong tg vuông bình phương đường cao hạ tử đỉnh góc vuông bằng tích giữa hai hình chiếu của 2 cạnh góc vuông trên cạnh huyền) (2)
Xét tg vuông ACH, c/m tương tự
\(NH^2=CN.AN\) (3)
Thay (2) và (3) vào (1)
(1) \(\Leftrightarrow\dfrac{AB^3}{AC^3}=\dfrac{BM.AM.MH}{CN.AN.NH}\)
Mà AM = NH; AN = MH (cmt)
\(\Rightarrow\dfrac{AB^3}{AC^3}=\dfrac{BM}{CN}\)

\(\dfrac{1}{\sqrt{x}+2}-\dfrac{2}{\sqrt{x}-2}-\dfrac{\sqrt{x}}{4-x}\left(\text{đ}k\text{x}\text{đ}:x\ge0;x\ne4\right)\\ =\dfrac{\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{2\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{\sqrt{x}-2-2\sqrt{x}-4-\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{-2\sqrt{x}-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{-2\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =-\dfrac{2}{\sqrt{x}-2}\)

\(\sqrt{x}-2+\dfrac{10-x}{\sqrt{x}+2}\left(ĐKXĐ:x\ge0\right)\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)}+\dfrac{10-x}{\sqrt{x}+2}\)
\(=\dfrac{x-4+10-x}{\sqrt{x}+2}\)
\(=\dfrac{6}{\sqrt{x}+2}\)
\(=\dfrac{6\left(\sqrt{x}-2\right)}{x-4}\)

\(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}+1\left(\text{đ}k\text{x}\text{đ}:x\ge0;x\ne1\right)\\=\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}+1-\left(\sqrt{x}-1\right)+\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\=\dfrac{\sqrt{x}+1-\sqrt{x}+1+x+\sqrt{x}-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\=\dfrac{x-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x+1}\right)}\\=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\=1\)

\(\dfrac{1}{\sqrt{3}-1}-\dfrac{1}{\sqrt{3}+1}\)
\(\Leftrightarrow\dfrac{\sqrt{3}+1}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}-\dfrac{\sqrt{3}-1}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
\(\Leftrightarrow\dfrac{\sqrt{3}+1-\sqrt{3}+1}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
\(\Leftrightarrow\dfrac{2}{3-1}\)
\(\Leftrightarrow1\)

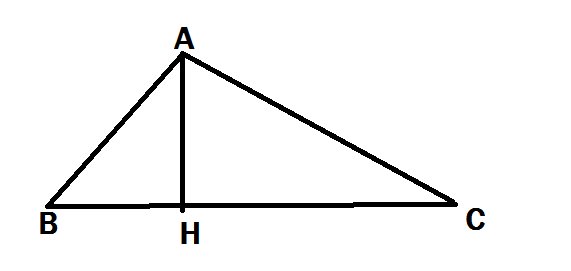
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{9}=\dfrac{1}{AB^2}+\dfrac{1}{25}\)
\(\Leftrightarrow\dfrac{1}{AB^2}=\dfrac{16}{225}\)
\(\Leftrightarrow AB=\dfrac{15}{4}\)
- \(AH.BC=AB.AC\)
\(3.BC=\dfrac{15}{4}.5\)
\(BC=6,25\)
- \(CH=\dfrac{AC^2}{BC}=4\)
=> BH = 6,25 - 4 = 2,25
\(\sqrt{x+3}\) + \(\sqrt{9x+27}\) - \(\sqrt{4x-12}\) = 10 đk \(x+3\) ≥ 0 ⇒ \(x\) ≥ -3
\(\sqrt{x+3}\) + \(\sqrt{9\left(x+3\right)}\) - \(\sqrt{4\left(x+3\right)}\) = 10
\(\sqrt{x+3}\) + 3\(\sqrt{x+3}\) - 2\(\sqrt{x+3}\) = 10
(1 + 3 - 2)\(\sqrt{x+3}\) = 10
2\(\sqrt{x+3}\) = 10
\(\sqrt{x+3}\) = 10: 2
\(\sqrt{x+3}\) = 5
\(x+3\) = 10
\(x\) = 10 - 3
\(x\) = 7 ( thỏa mãn)
Vậy \(x\) = 7