Gọi chiều dài màn hình là `x` (cm) 

ĐK: `x>0` 

Đổi: 17inch ≃ 43,18 (cm) 

Chiều cao màn hình là: `5/8x(cm)` 

Áp dụng định lý Pythagore ta có: 

\(x^2+\left(\dfrac{5}{8}x\right)^2=43,18^2\\ < =>x^2+\dfrac{25}{64}x^2=1864,5124\\ < =>\dfrac{79}{64}x^2=1864,5124\\ < =>x^2\approx1510,4\\ < =>x\approx38,9\left(cm\right)\left(x>0\right)\)

=> Chiều cao của màn hình là: `5/8*38,9≃24,3(cm)` 

Vậy: 

Gọi x (cm) là chiều rộng màn hình (x > 0)

Chiều dài màn hình là:

  Đổi 17 inch ≈ 43,2 cm

  Theo đề bài, ta có phương trình:

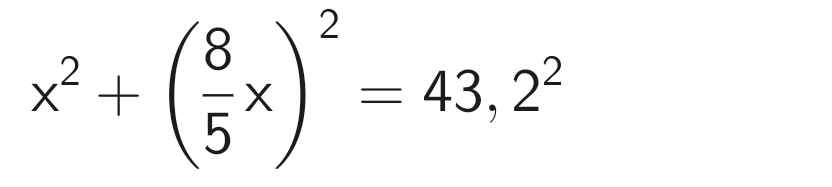
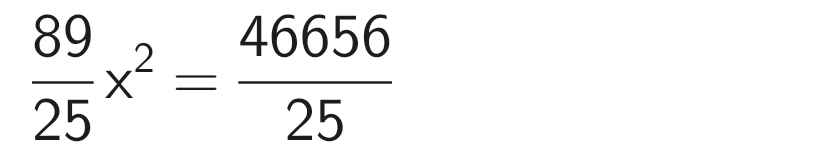
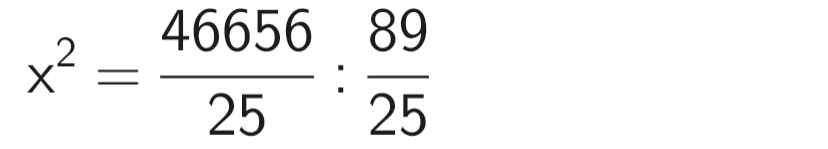
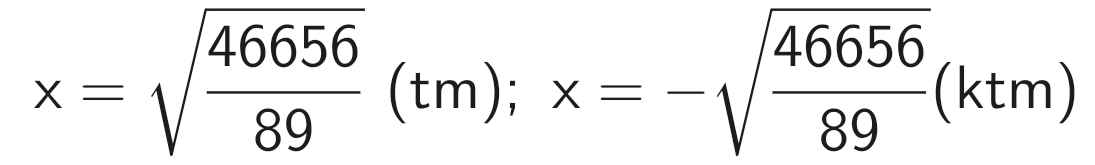
⇒ x ≈ 22,9 (cm)

Vậy chiều rộng màn hình là 22,9 cm, chiều dài màn hình là 22,9.1,6 ≈ 36,6 cm

Đa thức này thu gọn rồi bạn

Biểu thức này ko thu gọn được nữa em (đồng thời cũng ko phân tích được thành nhân tử)

\(\Leftrightarrow\left(x+5\right)^2-9\left(x+5\right)=0\)

\(\Leftrightarrow\left(x+5\right)\left(x+5-9\right)=0\)

\(\Leftrightarrow\left(x+5\right)\left(x-4\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=4\end{matrix}\right.\)

\(\left(x+5\right)^2-9x-45x=0\\ < =>\left(x^2+10x+25\right)-54x=0\\ < =>x^2+10x+25-54x=0\\ < =>x^2-44x+25=0\\ < =>\left(x^2-44x+484\right)-459=0\\ < =>\left(x-22\right)^2-459=0\\ < =>\left(x-22\right)^2=459\\ < =>\left[{}\begin{matrix}x-22=\sqrt{459}\\x-22=-\sqrt{459}\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=22+\sqrt{459}\\x=22-\sqrt{459}\end{matrix}\right.\)

a: Xét ΔMNP có \(\dfrac{MH}{MN}=\dfrac{MK}{MP}\)

nên HK//PN

Xét tứ giác NHKP có HK//NP

nên NHKP là hình thang

Hình thang NHKP có \(\widehat{HNP}=\widehat{KPN}\)(ΔMNP cân tại M)

nên NHKP là hình thang cân

a: Xét ΔNAM và ΔNCP có

NA=NC

\(\widehat{ANM}=\widehat{CNP}\)(hai góc đối đỉnh)

NM=NP

Do đó: ΔNAM=ΔNCP

=>\(\widehat{NAM}=\widehat{NCP}\)

=>CP//AM

=>CP//AB

b: Xét ΔNAP và ΔNCM có

NA=NC

\(\widehat{ANP}=\widehat{CNM}\)(hai góc đối đỉnh)

NP=NM

Do đó: ΔNAP=ΔNCM

=>\(\widehat{NAP}=\widehat{NCM}\)

=>AP//CM

c: Xét ΔABC có

M,N lần lượt là trung điểm của AB,AC

=>MN là đường trung bình của ΔABC

=>MN//BC và \(MN=\dfrac{BC}{2}\)

Ta có: BC=2MN

mà MP=2MN

nên BC=MP

Ta có: ΔNAM=ΔNCP

=>AM=CP

=>CP=BM

Xét ΔMBC và ΔCPM có

MB=CP

BC=PM

MC chung

Do đó: ΔMBC=ΔCPM

mình cần gấp áa

a: X,Y trái dấu

=>XY<0

=>\(-2abc^3\cdot3a^2b^3c^5< 0\)

=>\(-6a^3b^4c^8< 0\)

=>\(a^3>0\)

=>a>0

b: X,Y cùng dấu

=>X*Y>0

=>\(-2abc^3\cdot3a^2b^3c^5>0\)

=>\(-6a^3b^4c^8>0\)

=>\(a^3< 0\)

=>a<0

c: \(X\cdot Y=-5a^2n\cdot b\cdot3a^4n\cdot b^5=-15a^6n^2b^6< =0\forall a,b,n\)

=>X và Y không thể cùng có giá trị âm

\(x^2+xy-2x-2y\\ =\left(x^2+xy\right)-\left(2x+2y\right)\\ =x\left(x+y\right)-2\left(x+y\right)\\ =\left(x-2\right)\left(x+y\right)\)

\(P\left(x\right)=5x^2+x+2=5\left(x^2+\dfrac{1}{5}x\right)+2\\ =5\left(x^2+2.x.\dfrac{1}{10}+\left(\dfrac{1}{10}\right)^2\right)-5.\left(\dfrac{1}{10}\right)^2+2\\ =5\left(x+\dfrac{1}{10}\right)^2+\dfrac{39}{20}\)

Nhận xét: \(\left(x+\dfrac{1}{10}\right)^2\ge0\forall x\inℝ\\ \Rightarrow5\left(x+\dfrac{1}{10}\right)^2\ge0\\ \Rightarrow P\left(x\right)=5\left(x+\dfrac{1}{10}\right)^2+\dfrac{39}{20}\ge\dfrac{39}{20}\)

\(Min_{P\left(x\right)}=\dfrac{39}{20}\) tại \(\left(x+\dfrac{1}{10}\right)^2=0\Leftrightarrow x+\dfrac{1}{10}=0\Leftrightarrow x=-\dfrac{1}{10}\)