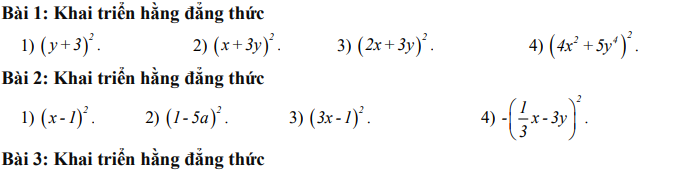
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi chiều dài màn hình là `x` (cm)
ĐK: `x>0`
Đổi: 17inch ≃ 43,18 (cm)
Chiều cao màn hình là: `5/8x(cm)`
Áp dụng định lý Pythagore ta có:
\(x^2+\left(\dfrac{5}{8}x\right)^2=43,18^2\\ < =>x^2+\dfrac{25}{64}x^2=1864,5124\\ < =>\dfrac{79}{64}x^2=1864,5124\\ < =>x^2\approx1510,4\\ < =>x\approx38,9\left(cm\right)\left(x>0\right)\)
=> Chiều cao của màn hình là: `5/8*38,9≃24,3(cm)`
Vậy:
Gọi x (cm) là chiều rộng màn hình (x > 0)
Chiều dài màn hình là:
 Đổi 17 inch ≈ 43,2 cm
Đổi 17 inch ≈ 43,2 cm
 Theo đề bài, ta có phương trình:
Theo đề bài, ta có phương trình:
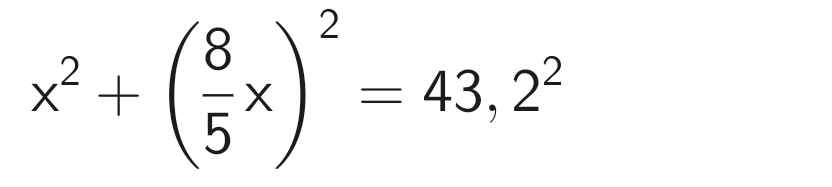
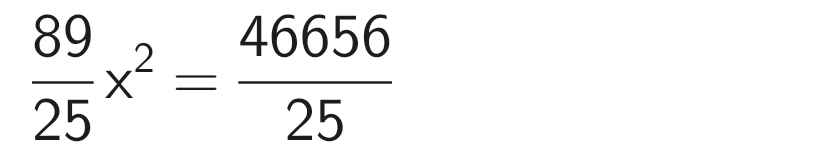
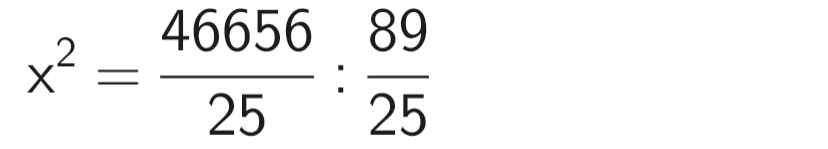

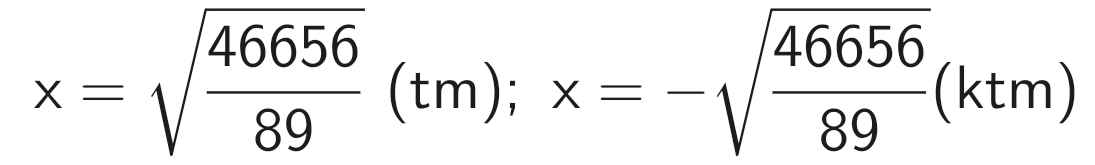
⇒ x ≈ 22,9 (cm)
Vậy chiều rộng màn hình là 22,9 cm, chiều dài màn hình là 22,9.1,6 ≈ 36,6 cm

Biểu thức này ko thu gọn được nữa em (đồng thời cũng ko phân tích được thành nhân tử)

\(\Leftrightarrow\left(x+5\right)^2-9\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x+5-9\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=4\end{matrix}\right.\)
\(\left(x+5\right)^2-9x-45x=0\\ < =>\left(x^2+10x+25\right)-54x=0\\ < =>x^2+10x+25-54x=0\\ < =>x^2-44x+25=0\\ < =>\left(x^2-44x+484\right)-459=0\\ < =>\left(x-22\right)^2-459=0\\ < =>\left(x-22\right)^2=459\\ < =>\left[{}\begin{matrix}x-22=\sqrt{459}\\x-22=-\sqrt{459}\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=22+\sqrt{459}\\x=22-\sqrt{459}\end{matrix}\right.\)

a: Xét ΔMNP có \(\dfrac{MH}{MN}=\dfrac{MK}{MP}\)
nên HK//PN
Xét tứ giác NHKP có HK//NP
nên NHKP là hình thang
Hình thang NHKP có \(\widehat{HNP}=\widehat{KPN}\)(ΔMNP cân tại M)
nên NHKP là hình thang cân

a: Xét ΔNAM và ΔNCP có
NA=NC
\(\widehat{ANM}=\widehat{CNP}\)(hai góc đối đỉnh)
NM=NP
Do đó: ΔNAM=ΔNCP
=>\(\widehat{NAM}=\widehat{NCP}\)
=>CP//AM
=>CP//AB
b: Xét ΔNAP và ΔNCM có
NA=NC
\(\widehat{ANP}=\widehat{CNM}\)(hai góc đối đỉnh)
NP=NM
Do đó: ΔNAP=ΔNCM
=>\(\widehat{NAP}=\widehat{NCM}\)
=>AP//CM
c: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{BC}{2}\)
Ta có: BC=2MN
mà MP=2MN
nên BC=MP
Ta có: ΔNAM=ΔNCP
=>AM=CP
=>CP=BM
Xét ΔMBC và ΔCPM có
MB=CP
BC=PM
MC chung
Do đó: ΔMBC=ΔCPM

a: X,Y trái dấu
=>XY<0
=>\(-2abc^3\cdot3a^2b^3c^5< 0\)
=>\(-6a^3b^4c^8< 0\)
=>\(a^3>0\)
=>a>0
b: X,Y cùng dấu
=>X*Y>0
=>\(-2abc^3\cdot3a^2b^3c^5>0\)
=>\(-6a^3b^4c^8>0\)
=>\(a^3< 0\)
=>a<0
c: \(X\cdot Y=-5a^2n\cdot b\cdot3a^4n\cdot b^5=-15a^6n^2b^6< =0\forall a,b,n\)
=>X và Y không thể cùng có giá trị âm

\(x^2+xy-2x-2y\\ =\left(x^2+xy\right)-\left(2x+2y\right)\\ =x\left(x+y\right)-2\left(x+y\right)\\ =\left(x-2\right)\left(x+y\right)\)

Bài 1:
\(1,\left(y+3\right)^2\\ =y^2+2\cdot y\cdot3+3^2\\ =y^2+6y+9\\ 2,\left(x+3y\right)^2\\ =x^2+2\cdot x\cdot3y+\left(3y\right)^2\\ =x^2+6xy+9y^2\\ 3,\left(2x+3y\right)^2\\ =\left(2x\right)^2+3\cdot2x\cdot3y+\left(3y\right)^2\\ =4x^2+18xy+9y^2\\ 4,\left(4x^2+5y^4\right)\\ =\left(4x^2\right)^2+2\cdot4x^2\cdot5y^4+\left(5y^4\right)^2\\ =16x^4+40x^2y^4+25y^8\)
Bài 2:
\(1,\left(x-1\right)^2\\ =x^2-2\cdot x\cdot1+1^2\\ =x^2-2x+1\\ 2,\left(1-5a\right)^2\\ =1^2-2\cdot1\cdot5a+\left(5a\right)^2\\ =1-10a+25a^2\\ 3,\left(3x-1\right)^2\\ =\left(3x\right)^2-2\cdot3x\cdot1+1^2\\ =9x^2-6x+1\\ 4,-\left(\dfrac{1}{3}x-3y\right)^2\\ =-\left[\left(\dfrac{1}{3}x\right)^2-2\cdot\dfrac{1}{3}x\cdot3y+\left(3y\right)^2\right]\\ =-\left(\dfrac{1}{9}x^2-2xy+9y^2\right)\\ =-\dfrac{1}{9}x^2+2xy-9y^2\)