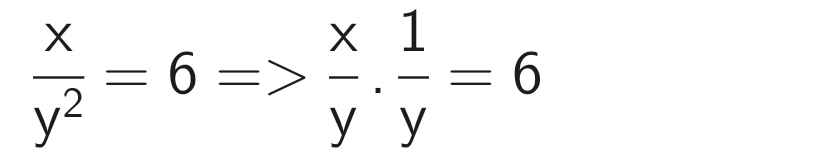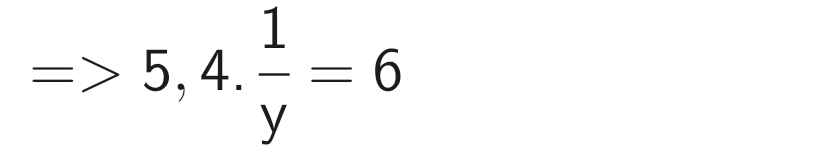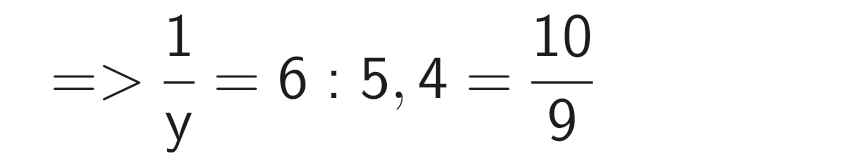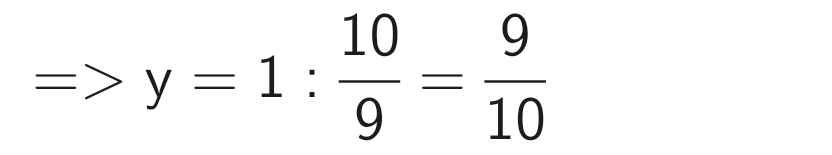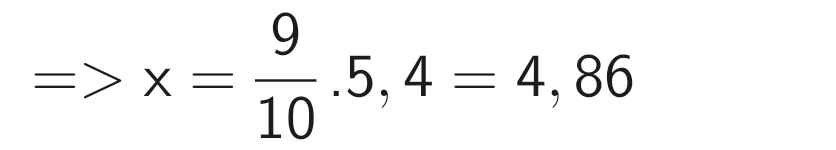Alexis, Emma, and Li play in the school band. One plays the
flute. One plays the saxophone. One plays the drums. Alexis is
a 6" grader. Alexis and the saxophone player practice together
after school. Emma and the flute player are 5" graders. Who
plays the drums?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
so sánh M và N biết: M=\(\dfrac{100^{100}+1}{100^{99}+1}\) và N=\(\dfrac{100^{101}+1}{100^{100}+1}\)

\(\dfrac{M}{100}=\dfrac{100^{100}+1}{100.\left(100^{99}+1\right)}=\dfrac{100^{100}+1}{100^{100}+100}=\dfrac{100^{100}+100-99}{100^{100}+100}=1-\dfrac{99}{100^{100}+100}\)
\(\dfrac{N}{100}=\dfrac{100^{101}+1}{100.\left(100^{100}+1\right)}=\dfrac{100^{101}+1}{100^{101}+100}=\dfrac{100^{101}+100-99}{100^{101}+100}=1-\dfrac{99}{100^{101}+100}\)
Do \(100^{101}>100^{100}\)nên \(100^{101}+100>100^{100}+100\)
\(\Rightarrow-\dfrac{99}{100^{101}+100}>-\dfrac{99}{100^{100}+100}\)
\(\Rightarrow\dfrac{M}{100}>\dfrac{N}{100}\Rightarrow M>N\)

1,8dm=18cm
Diện tích đáy là: \(S_{Đáy}=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
Thể tích hình lăng trụ là: \(6\cdot18=108\left(cm^3\right)\)
Chu vi đáy là 3+4+5=12(cm)
Diện tích xung quanh là: \(12\cdot18=216\left(cm^2\right)\)
Diện tích toàn phần là: \(216+6\cdot2=216+12=228\left(cm^2\right)\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\dfrac{x+y+z-1-2-3}{2+3+4}=\dfrac{-34-6}{9}=\dfrac{-40}{9}\)
=>\(\left\{{}\begin{matrix}x-1=-\dfrac{40}{9}\cdot2=-\dfrac{80}{9}\\y-2=-\dfrac{40}{9}\cdot3=-\dfrac{120}{9}\\z-3=-\dfrac{40}{9}\cdot4=-\dfrac{160}{9}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{80}{9}+1=-\dfrac{71}{9}\\y=-\dfrac{120}{9}+2=-\dfrac{120}{9}+\dfrac{18}{9}=-\dfrac{102}{9}\\z=-\dfrac{160}{9}+3=-\dfrac{160}{9}+\dfrac{27}{9}=-\dfrac{133}{9}\end{matrix}\right.\)

\(3^{12}=3^{3.4}=\left(3^3\right)^4=27^4\)
\(5^8=5^{2.4}=\left(5^2\right)^4=25^4\)
Do \(27^4>25^4\) nên \(3^{12}>5^8\)

\(\dfrac{15}{2}-5\cdot\left(-\dfrac{3}{2}\right)^2:\dfrac{2}{9}+\left(-\dfrac{2}{3}\right)^2\)
\(=\dfrac{15}{2}-5\cdot\dfrac{9}{4}\cdot\dfrac{9}{2}+\dfrac{4}{9}\)
\(=\dfrac{15}{2}-\dfrac{405}{8}+\dfrac{4}{9}=-\dfrac{3073}{72}\)

\(\dfrac{x}{y}\) = 5,4 và \(\dfrac{x}{y^2}\) = 6 (y ≠ 0)
(\(\dfrac{x}{y}\)) = 5,42 ⇒ \(\left(\dfrac{x}{y}\right)^2\)= 29,16;
Thay \(\dfrac{x}{y^2}\) = 6 vào biểu thức (\(\dfrac{x}{y}\))2 = 29,16 ta được:
\(x.\)6 = 29,16 ⇒ \(x=\) 29,16 : 6 ⇒ \(x\) = 4,86
Thay \(x=4,86\) vào biểu thức \(\dfrac{x}{y}\) = 5,4 ta được
\(4,86\) : y = 5,4 ⇒ y = 4,86 : 5,4 ⇒ y = 0,9
Vậy (\(x;y\)) = (4,86; 0,9)

`(x-3)(x+4) > 0`
`=> x - 3` và `x + 4` cùng dấu
Trường hợp 1: `{(x-3>0),(x+4>0):}`
`=> {(x>3),(x>-4):}`
`=> x > 3`
Trường hợp 2: `{(x-3<0),(x+4<0):}`
`=> {(x<3),(x<-4):}`
`=> x < -4`
Vậy ...
a; (\(x-3\))(\(x+4\)) > 0
\(x-3=0\) ⇒ \(x=3\)
\(x+4\) = 0 ⇒ \(x=-4\)
Lập bảng ta có:
| \(x\) | - 4 3 |
| \(x-3\) | - - 0 + |
| \(x+4\) | - 0 + + |
| (\(x-3\))(\(x+4\)) | + 0 - 0 + |
Theo bảng trên ta có:
\(x\) \(\in\) (- ∞; -4) \(\cup\)(3 ; + ∞)

30.(\(x-\dfrac{7}{12}\)) - 24\(x\) = 100 + 6.(\(x\) - \(\dfrac{3}{4}\))
30\(x\) - \(\dfrac{35}{2}\) - 24\(x\) = 100 + 6\(x\) - \(\dfrac{9}{2}\)
30\(x\) - 24\(x\) - 6\(x\) = 100 - \(\dfrac{9}{2}\) + \(\dfrac{35}{2}\)
6\(x\) - 6\(x\) = 100 - (\(\dfrac{9}{2}\) - \(\dfrac{35}{2}\))
0 = 100 + 13
0 = 113 (vô lý)
Vậy không có giá trị nào của \(x\) thỏa mãn đề bài.