1 người 1 tháng nhận 9.600.000 lương.1/8 số tiền người đó dùng thuê nhà.2/3 số tiền để ăn uống.tiền còn lại anh để dành.hỏi 1 tháng anh để dành được bao nhiêu tiền?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\dfrac{\sqrt{2}\left(2+\sqrt{3}\right)}{2+\sqrt{4+2\sqrt{3}}}+\dfrac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\sqrt{4-2\sqrt{3}}}\)
\(=\dfrac{\sqrt{2}\left(2+\sqrt{3}\right)}{2+\sqrt{\left(\sqrt{3}+1\right)^2}}+\dfrac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\sqrt{\left(\sqrt{3}-1\right)^2}}\)
\(=\dfrac{\sqrt{2}\left(2+\sqrt{3}\right)}{2+\sqrt{3}+1}+\dfrac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\left(\sqrt{3}-1\right)}=\sqrt{2}\left(\dfrac{2+\sqrt{3}}{3+\sqrt{3}}+\dfrac{2-\sqrt{3}}{3-\sqrt{3}}\right)\)
\(=\sqrt{2}\left(\dfrac{\left(2+\sqrt{3}\right)\left(3-\sqrt{3}\right)+\left(2-\sqrt{3}\right)\left(3+\sqrt{3}\right)}{\left(3+\sqrt{3}\right)\left(3-\sqrt{3}\right)}\right)\)
\(=\sqrt{2}\left(\dfrac{6}{9-3}\right)=\sqrt{2}\)

- Tiểu học -
Tổng chiều dài và chiều rộng miếng đất đó là:
` 1400 : 2 = 700 (m)`
Ta có sơ đồ:
Chiều dài: 4 phần
Chiều rộng: 3 phần
Tổng số phần bằng nhau là:
`3+4=7` (phần)
Giá trị 1 phần là:
`700 : 7 = 100 (m)`
Chiều dài miếng đất là:
`100` x `4 = 400 (m)`
Chiều rộng miếng đất là:
`100 ` x `3 = 300 (m)`
Diện tích miếng đất là:
`400` x `300 = 120000 (m^2)`
- Cấp 2 dưới lớp 9 -
Gọi chiều rộng của miếng đất là `x (m)`
Điều kiện: `1440> x > 0 `
=> Chiều dài miếng đất là: \(\dfrac{4}{3}\) `x `
Do chu vi của miếng đất là 1400m nên:
`(x +` \(\dfrac{4}{3}\) `x) . 2 = 1400`
`=>` \(\dfrac{7}{3}\) `x = 700`
`=> x = 300` (Thỏa mãn)
Vậy chiều rộng miếng đất là `300m`
CHiều dài miếng đất là:
`300 . 4 : 3 = 400 (m)`
Diện tích miếng đất là:
`400 . 300 = 120000 (m^2)`


\(E=2x^2+4x+13\)
\(=2\left(x^2+2x+\dfrac{13}{2}\right)\)
\(=2\left(x^2+2x+1+\dfrac{11}{2}\right)\)
\(=2\left(x+1\right)^2+11>=11>0\forall x\)
\(F=2x^2-3x+6\)
\(=2\left(x^2-\dfrac{3}{2}x+3\right)\)
\(=2\left(x^2-2\cdot x\cdot\dfrac{3}{4}+\dfrac{9}{16}+\dfrac{39}{16}\right)\)
\(=2\left(x-\dfrac{3}{4}\right)^2+\dfrac{39}{8}>=\dfrac{39}{8}>0\forall x\)
E=2x2+4x+13
E=2(x2+2x+1)+11
E=2(x+1)2+11
2(x+1)2≥0,∀x
⇒2(x+1)2+11 lớn hơn 0 ∀x
⇒E luôn nhân giá trị dương
F=2x2-3x+6
2F=4x2-6x+12
2F=(4x2-6x+\(\dfrac{9}{4}\))+\(\dfrac{15}{4}\)
2F=(2x+\(\dfrac{3}{2}\))2+\(\dfrac{15}{4}\)
F=\(\dfrac{\left(2x+\dfrac{3}{2}\right)^2}{2}\)+\(\dfrac{15}{8}\)
\(\dfrac{\left(2x+\dfrac{3}{2}\right)^2}{2}\)≥0,∀x
⇒\(\dfrac{\left(2x+\dfrac{3}{2}\right)^2}{2}\)+\(\dfrac{15}{8}\) lớn hơn 0 ∀x
⇒F luôn nhận giá trị dương

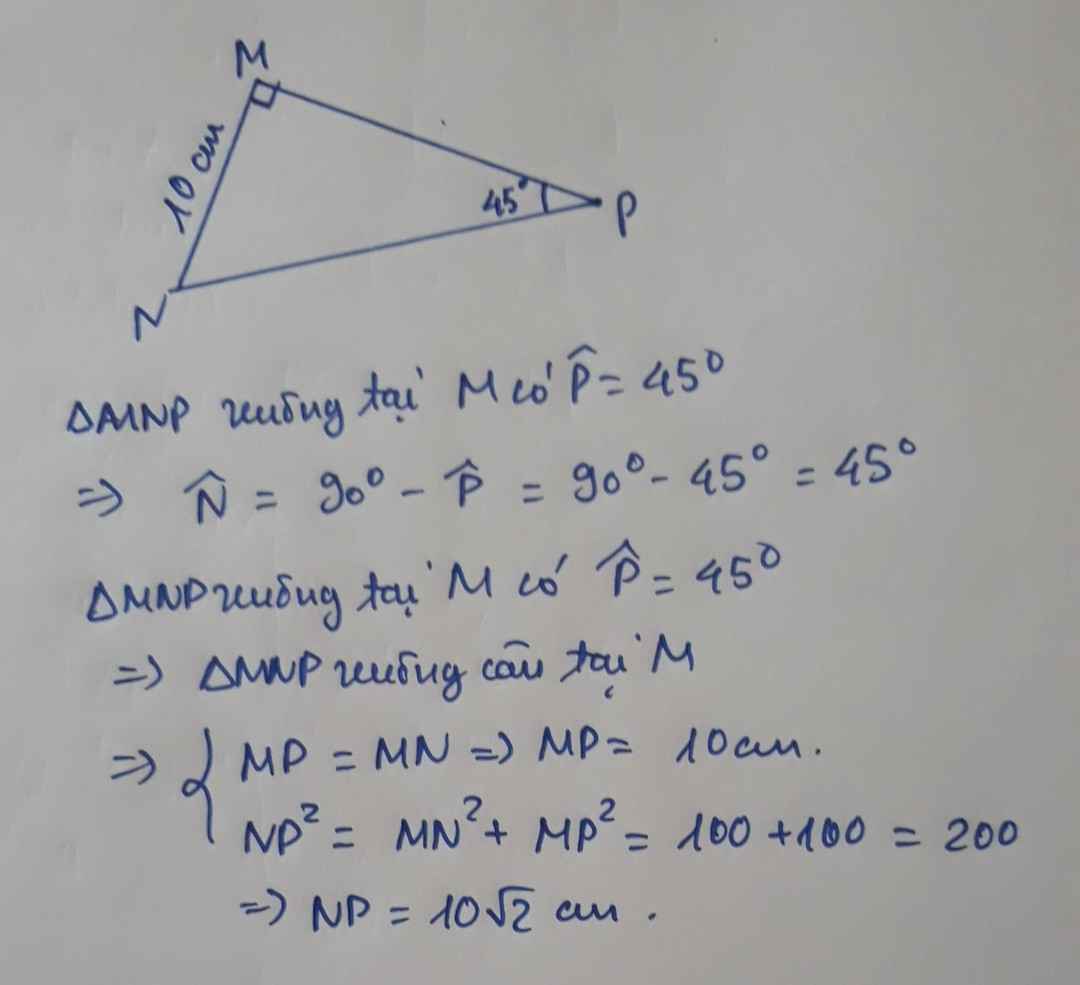
ΔMNP vuông tại M
=>\(\widehat{MNP}+\widehat{P}=90^0\)
=>\(\widehat{N}=90^0-45^0=45^0\)
Xét ΔMNP vuông tại M có \(tanP=\dfrac{MN}{MP}\)
=>\(\dfrac{10}{MP}=tan45=1\)
=>MP=10(cm)
ΔMNP vuông tại M
=>\(MN^2+MP^2=NP^2\)
=>\(NP=\sqrt{10^2+10^2}=10\sqrt{2}\left(cm\right)\)

\(5^2\cdot x-2^4\cdot x=3^4-6\cdot3^2\\ \Rightarrow25x-16x=81-6\cdot9\\ \Rightarrow9x=81-54\\ \Rightarrow9x=27\\ \Rightarrow x=27:9\\ \Rightarrow x=3\)
\(5^2\cdot x-2^4\cdot x=3^4-6\cdot3^2\)
=>\(25x-16x=81-6\cdot9=81-54=27\)
=>9x=27
=>x=3



a: Xét ΔAEH vuông tại E và ΔAHB vuông tại H có
\(\widehat{EAH}\) chung
Do đó: ΔAEH~ΔAHB
=>\(\dfrac{AE}{AH}=\dfrac{AH}{AB}\)
=>\(AH^2=AE\cdot AB\left(1\right)\)
Xét ΔAFH vuông tại F và ΔAHC vuông tại H có
\(\widehat{FAH}\) chung
Do đó: ΔAFH~ΔAHC
=>\(\dfrac{AF}{AH}=\dfrac{AH}{AC}\)
=>\(AH^2=AF\cdot AC\left(2\right)\)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
b: Xét tứ giác AEHF có \(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
nên AEHF là hình chữ nhật
=>\(HA^2=HE^2+HF^2\)
Xét ΔEHA vuông tại H và ΔEBH vuông tại E có
\(\widehat{EHA}=\widehat{EBH}\left(=90^0-\widehat{HAE}\right)\)
Do đó: ΔEHA~ΔEBH
=>\(\dfrac{EH}{EB}=\dfrac{EA}{EH}\)
=>\(EH^2=EA\cdot EB\)
Xét ΔFHA vuông tại F và ΔFCH vuông tại F có
\(\widehat{FHA}=\widehat{FCH}\left(=90^0-\widehat{HAC}\right)\)
Do đó: ΔFHA~ΔFCH
=>\(\dfrac{FH}{FC}=\dfrac{FA}{FH}\)
=>\(FH^2=FA\cdot FC\)
\(HA^2=HE^2+HF^2=EA\cdot EB+FA\cdot FC\)
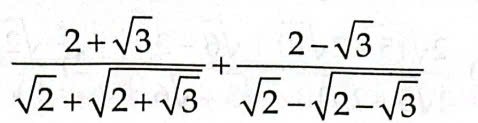
X là số có hai chữ số và lớn hơn 15;
Là gì vậy mọi người
X là số có ba chữ số và bé hơn 105;