
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Thay tọa độ điểm A(-1; 3) vào hàm số, ta có:
\(\left(m-1\right).\left(-1\right)+2=3\)
\(\Leftrightarrow-m+1+2=3\)
\(\Leftrightarrow-m=3-1-2\)
\(\Leftrightarrow m=0\)
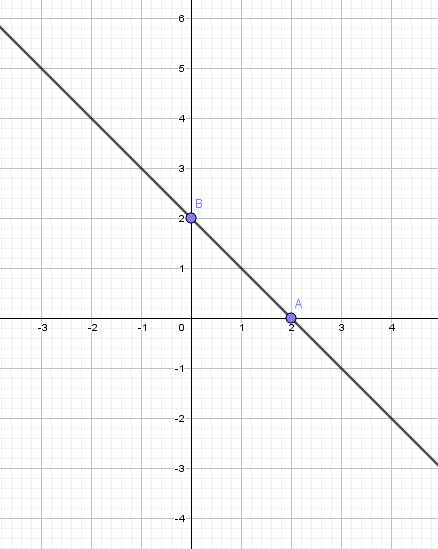
\(\Rightarrow y=-x+2\)
b)
| \(x\) | \(0\) | \(2\) |
| \(y=-x+2\) | \(2\) | \(0\) |
Đồ thị:

y³ - 8 - 6y(y - 2)
= (y³ - 8) - 6y(y - 2)
= (y - 2)(y² + 2y + 4) - 6y(y - 2)
= (y - 2)(y² + 2y + 4 - 6y)
= (y - 2)(y² - 4y + 4)
= (y - 2)(y - 2)²
= (y - 2)³
y³ - 8 - 6y(y - 2)
= (y³ - 8) - 6y(y - 2)
= (y - 2)(y² + 2y + 4) - 6y(y - 2)
= (y - 2)(y² + 2y + 4 - 6y)
= (y - 2)(y² - 4y + 4)
= (y - 2)(y - 2)²

P = \(\dfrac{2x+3}{x+3}\) (đk \(x\ne\) - 3; \(x\in\) Z-
P \(\in\) Z ⇔ 2\(x\) + 3 ⋮ \(x\) + 3
2\(x\) + 6 -3 ⋮ \(x\) + 3
2.(\(x\) + 3) - 3 ⋮ \(x\) + 3
3 \(⋮\) \(x\) + 3
\(x\) + 3 \(\in\) Ư(3) = {-3; -1; 1; 3}
Lập bảng ta có:
| \(x\) + 3 | - 3 | -1 | 1 | 3 |
| \(x\) | -6 | -4 | -2 | 0 |
Vì \(x\) \(\in\) Z- nên theo bảng trên ta có:
\(x\) \(\in\) {- 6; - 4; -2}


Lời giải:
b. Ta thấy: $5^2+12^2=13^2$ hay $AB^2+AC^2=BC^2$ nên tam giác $ABC$ vuông tại $A$.
Tứ giác $ACEB$ có 2 đường chéo $BC,AE$ cắt nhau tại trung điểm $D$ của mỗi đường nên là hình bình hành.
Mà $\widehat{A}=90^0$ nên $ACEB$ là hình chữ nhật.
a.
$ACEB$ là hcn nên $AE=BC=13$ (cm)
$\Rightarrow AD=AE:2=13:2=6,5$ (cm)
c.
Để $ABEC$ là hình vuông thì $AB=AC$. Khi đó $ABC$ phải là tam giác vuông cân tại A chứ không liên quan gì đến điểm D hết bạn nhé.

Bài 4:
Quãng đường bạn An đi: $BD$
Quãng đường bạn Hải đi: $CD$
Do $AB\parallel NC$ nên áp dụng định lý Talet, tỉ số quãng đường bạn An đi so với bạn Hải đi là:
$\frac{BD}{CD}=\frac{AB}{NC}=\frac{AB}{AM}=\frac{1}{2}$
Vậy bạn An đi quãng đường bằng 1/2 quãng đường Hải đi
Mà vận tốc 2 bạn như nhau nên thời gian An đi bằng 1/2 thời gian Hải đi
Bạn An đến D lúc 8h, xuất phát từ 7h30 nên thời gian An đi là: 8h-7h30'=30'=0,5h
Thời gian Hải đi để đến gặp An lúc 8h là: $0,5.2=1$ (h)
Vậy Hải phải xuất phát lúc: $8h-1h=7h$
Bài 3:
a. Xét tam giác $ADC$ có $MP\parallel DC$ nên áp dụng định lý Talet:
$\frac{AM}{MD}=\frac{AP}{PC}(1)$
Xét tam giác $ACB$ có $PN\parallel AB$ nên áp dụng định lý Talet:
$\frac{AP}{PC}=\frac{BN}{NC}(2)$
Từ $(1); (2)\Rightarrow \frac{AM}{MD}=\frac{BN}{NC}$
b.
Áp dụng định lý Talet với tam giác $ADC$, $MP\parallel DC$:
$\frac{MP}{DC}=\frac{AM}{AD}=\frac{AM}{AM+MD}=\frac{AM}{AM+2AM}=\frac{1}{3}$
$\Rightarrow MP=DC:3=6:3=2$ (cm)
Theo kết quả phần a:
$\frac{BN}{NC}=\frac{AM}{MD}=\frac{AM}{2AM}=\frac{1}{2}$
$\Rightarrow NC=2BN$
Áp dụng định lý Talet cho tam giác $ACB$, có $PN\parallel AB$:
$\frac{PN}{AB}=\frac{CN}{CB}=\frac{CN}{CN+BN}=\frac{2BN}{2BN+BN}=\frac{2}{3}$
$\Rightarrow PN=\frac{2}{3}AB=\frac{2}{3}.4=\frac{8}{3}$ (cm)
$MN=MP+PN=2+\frac{8}{3}=\frac{14}{3}$ (cm)

Ta có
\(\dfrac{BM}{AM}=\dfrac{BC}{AC}=\dfrac{a}{b}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
\(\dfrac{CN}{AN}=\dfrac{BC}{AB}=\dfrac{a}{b}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
\(\Rightarrow\dfrac{BM}{AM}=\dfrac{CN}{AN}\Rightarrow\dfrac{BM}{CN}=\dfrac{AM}{AN}\) => MN//BC (Talet)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MN}{BC}\Rightarrow\dfrac{AM}{b}=\dfrac{MN}{a}\) (1)
Ta có
\(\dfrac{AM}{BM}=\dfrac{AC}{BC}=\dfrac{b}{a}\) (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
\(\Rightarrow\dfrac{AM}{b}=\dfrac{BM}{a}=\dfrac{AM+BM}{a+b}=\dfrac{AB}{a+b}=\dfrac{b}{a+b}\)
\(\Rightarrow AM=\dfrac{b^2}{a+b}\) Thay vào (1)
\(\Rightarrow\dfrac{\dfrac{b^2}{a+b}}{b}=\dfrac{MN}{a}\Rightarrow\dfrac{b}{a+b}=\dfrac{MN}{a}\Rightarrow MN=\dfrac{ab}{a+b}\)
Ta có
����=����=��AMBM=ACBC=ba (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
����=����=��ANCN=ABBC=ba (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
⇒����=����⇒����=����⇒AMBM=ANCN⇒CNBM=ANAM => MN//BC (Talet)
⇒����=����⇒���=���⇒ABAM=BCMN⇒bAM=aMN (1)
Ta có
����=����=��BMAM=BCAC=ab (Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy)
⇒���=���=��+���+�=���+�=��+�⇒bAM=aBM=a+bAM+BM=a+bAB=a+bb
⇒��=�2�+�⇒AM=a+bb2 Thay vào (1)
⇒�2�+��=���⇒��+�=���⇒��=���+�⇒ba+bb2=aMN⇒a+bb=aMN⇒MN=a+bab

3x² + 2x - 1
= 3x² + 3x - x - 1
= (3x² + 3x) - (x + 1)
= 3x(x + 1) - (x + 1)
= (x + 1)(3x - 1)


a) Thay tọa độ điểm M(0; 5) vào đường thẳng, ta có:
\(m.0+5=5\)
Vậy đường thẳng đã cho luôn đi qua điểm M(0; 5) với mọi giá trị của m
b) Thay tọa độ điểm P(2; 2021) vào đường thẳng, ta có:
\(\left(2m-1\right).2-4m+2023=4m-2-4m+2023=2021\)
Vậy đường thẳng đã cho luôn đi qua P(2; 2021) với mọi giá trị của m