Từ điểm \(A\) ở ngoài đường tròn \(\left(O\right)\), kẻ hai tiếp tuyến \(AB\), \(AC\) với đường tròn \(\left(O\right)\) (\(B\), \(C\) là hai tiếp điểm). Kẻ cát tuyến \(ADE\) với \(\left(O\right)\) không đi qua \(O\) (\(D\) nằm giữa \(A\) và \(E\)). Gọi \(H\) là giao điểm của \(OA\) và \(BC\).
\(a\)) Chứng minh \(OD^2=OH\cdot OA\). Từ đó suy ra tam giác \(OHD\) đồng dạng với tam giác \(ODA\).
\(b\)) Gọi \(I\) là giao điểm của \(BC\) và \(AE\). Chứng minh \(HI\) là phân giác của góc \(DHF\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\sqrt{\dfrac{11}{540}}\)
\(=\dfrac{\sqrt{11}}{\sqrt{540}}\)
\(=\dfrac{\sqrt{11}}{\sqrt{6^2\cdot15}}\)
\(=\dfrac{\sqrt{11}}{6\sqrt{15}}\)
\(=\dfrac{\sqrt{11}\cdot\sqrt{15}}{6\sqrt{15}\cdot\sqrt{15}}\)
\(=\dfrac{\sqrt{165}}{6\cdot15}\)
\(=\dfrac{\sqrt{165}}{90}\)

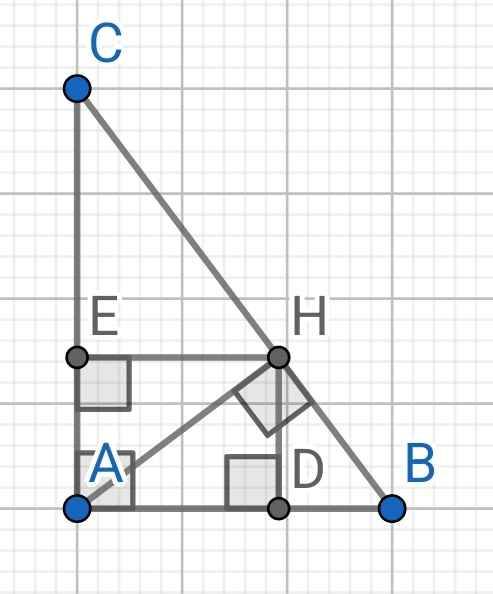 1) ∆ABC vuông tại A, AH là đường cao
1) ∆ABC vuông tại A, AH là đường cao
⇒ AH² = BH.CH = 4.9 = 36
⇒ AH = 6 (cm)
tanB = AH/BH = 6/4 = 3/2
⇒ ∠B ≈ 56⁰
2) a)
Do D, E lần lượt hình chiếu của H lên AB, AC
⇒ HD ⊥ AB và HE ⊥ AC
Tứ giác ADHE có:
∠HEA = ∠EAD = ∠ADH = 90⁰
⇒ ADHE là hình chữ nhật

DK: a≥0
Với dk ta có \(a+1\ge2\sqrt{a}\Leftrightarrow\dfrac{2\sqrt{a}}{a+1}\le1\)
Vậy GTLN của D là 1 khi a=1(Bất đẳng thức Cô si)

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.

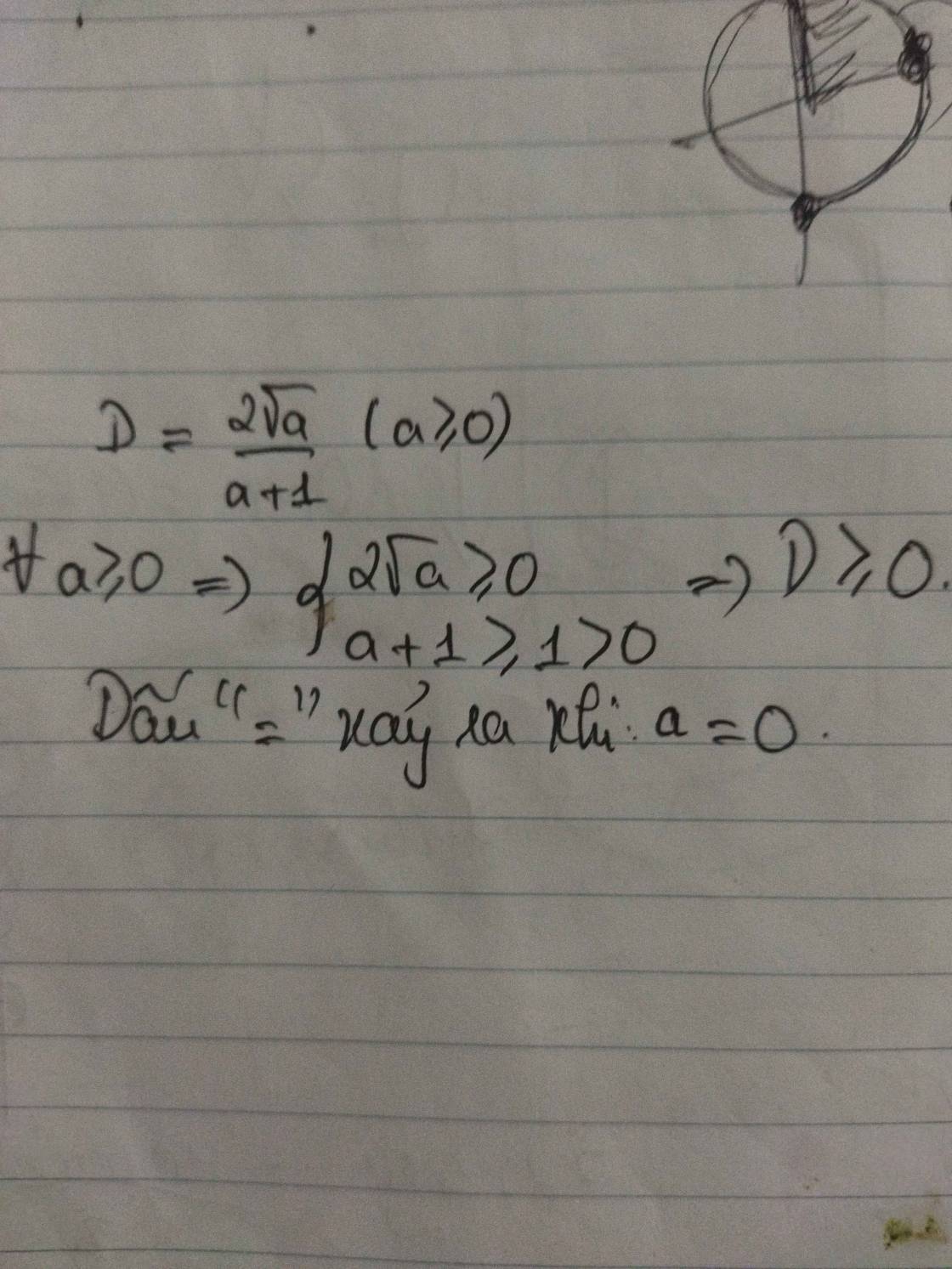

a) Do AB, AC tiếp xúc (O) tại B, C nên \(\widehat{OBA}=90^o\) và \(OA\perp BC\) tại H.
Xét tam giác OAB vuông tại B có đường cao BH, ta có \(OB^2=OA.OH\)
Mà \(OB=OD\left(=R_{\left(O\right)}\right)\) nên \(OD^2=OA.OH\). Từ đó suy ra \(\dfrac{OD}{OA}=\dfrac{OH}{OD}\). Từ đó dễ dàng suy ra 2 tam giác OHD và ODA đồng dạng.
b) Tam giác OAB vuông tại B có đường cao BH nên \(AB^2=AH.AO\)
Mặt khác, ta có \(\widehat{ABD}=\widehat{AEB}\) vì chúng lần lượt là góc tạo bởi tiếp tuyến, dây cung và góc nội tiếp cùng chắn cung BD.
\(\Rightarrow\Delta ABD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\Rightarrow AB^2=AD.AE\)
Từ đó suy ra \(AH.AO=AD.AE\) hay \(\dfrac{AH}{AD}=\dfrac{AE}{AO}\). Do đó \(\Delta AHE~\Delta ADO\left(c.g.c\right)\) \(\Rightarrow\widehat{AEH}=\widehat{AOD}\) hay tứ giác OHDE nội tiếp.
\(\Rightarrow\widehat{AHD}=\widehat{DEO}=\widehat{ODE}=\widehat{OHE}\)
\(\Rightarrow90^o-\widehat{AHD}=90^o-\widehat{OHE}\) \(\Rightarrow\widehat{DHI}=\widehat{EHI}\).
Ta suy ra được đpcm.