với x, y, z >0, chứng minh (x2 + 1)(y2 + 1)(z2 + 1) ≥\(\dfrac{3}{4}\)(x+y+z)2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(x+y+z=1\Rightarrow z=1-x-y\)
Khi đó: \(xy+z=xy+1-x-y\)
\(=x\left(y-1\right)-\left(y-1\right)=\left(x-1\right)\left(y-1\right)\) (1)
Tương tự, ta cũng có: \(\left\{{}\begin{matrix}yz+x=\left(y-1\right)\left(z-1\right)\\zx+y=\left(z-1\right)\left(x-1\right)\end{matrix}\right.\) (2)
Lại có: \(x+y+z=1\Rightarrow\left\{{}\begin{matrix}x+y=1-z\\y+z=1-x\\z+x=1-y\end{matrix}\right.\) (3)
Thay (1); (2) và (3) vào \(T\), ta được:
\(T=\dfrac{\left[\left(x-1\right)\left(y-1\right)\right]\left[\left(y-1\right)\left(z-1\right)\right]\left[\left(z-1\right)\left(x-1\right)\right]}{\left(1-z\right)^2\left(1-x\right)^2\left(1-y\right)^2}\)
\(=\dfrac{\left(x-1\right)^2\left(y-1\right)^2\left(z-1\right)^2}{\left(x-1\right)^2\left(y-1\right)^2\left(z-1\right)^2}=1\)
Vậy \(T=1\).

a: Xét ΔHBA vuông tại H và ΔHCB vuông tại H có
\(\widehat{HBA}=\widehat{HCB}\left(=90^0-\widehat{HAB}\right)\)
Do đó: ΔHBA~ΔHCB
=>\(\dfrac{HB}{HC}=\dfrac{HA}{HB}\)
=>\(HB^2=HA\cdot HC\)
b: Ta có: HM\(\perp\)BA
BC\(\perp\)BA
Do đó: HM//BC
Xét ΔAMH vuông tại M và ΔHNC vuông tại N có
\(\widehat{MHA}=\widehat{NCH}\)(hai góc đồng vị, MH//BC)
Do đó: ΔAMH~ΔHNC
c: Xét tứ giác BMHN có \(\widehat{BMH}=\widehat{BNH}=\widehat{MBN}=90^0\)
nên BMHN là hình chữ nhật
=>\(\widehat{NMH}=\widehat{NBH}\)
mà \(\widehat{NBH}=\widehat{BAC}\left(=90^0-\widehat{C}\right)\)
nên \(\widehat{NMH}=\widehat{BAC}\)
Ta có: BMHN là hình chữ nhật
=>\(\widehat{MNH}=\widehat{MBH}\)
mà \(\widehat{MBH}=\widehat{C}\left(=90^0-\widehat{A}\right)\)
nên \(\widehat{MNH}=\widehat{C}\)
Ta có: ΔCHN vuông tại N
mà NI là đường trung tuyến
nên IN=IH
=>ΔINH cân tại I
=>\(\widehat{INH}=\widehat{IHN}\)
mà \(\widehat{IHN}=\widehat{A}\)(hai góc đồng vị, NH//AB)
nên \(\widehat{INH}=\widehat{A}\)
Ta có: ΔHMA vuông tại M
mà MK là đường trung tuyến
nên KH=KM
=>ΔKHM cân tại K
=>\(\widehat{KMH}=\widehat{KHM}\)
mà \(\widehat{KHM}=\widehat{C}\)(hai góc đồng vị, MH//BC)
nên \(\widehat{KMH}=\widehat{C}\)
\(\widehat{INM}=\widehat{INH}+\widehat{MNH}=\widehat{C}+\widehat{A}=90^0\)
=>IN\(\perp\)NM(1)
\(\widehat{KMN}=\widehat{KMH}+\widehat{NMH}=\widehat{C}+\widehat{A}=90^0\)
=>NM\(\perp\)MK(2)
Từ (1),(2) suy ra MK//NI
Xét tứ giác KMNI có MK//NI
nên KMNI là hình thang
Hình thang KMNI có IN\(\perp\)NM
nên KMNI là hình thang vuông

a: Xét ΔABC có DE//BC
nên \(\dfrac{DE}{BC}=\dfrac{AD}{AB}\)
=>\(\dfrac{DE}{8}=\dfrac{2}{5}\)
=>\(DE=8\cdot\dfrac{2}{5}=3,2\left(cm\right)\)
b: Xét tứ giác BDFC có
BD//FC
DF//BC
Do đó: BDFC là hình bình hành
=>DF=BC=8cm
DE+EF=DF
=>EF+3,2=8
=>EF=4,8(cm)
Xét ΔIFE và ΔIBC có
\(\widehat{IFE}=\widehat{IBC}\)(hai góc so le trong, FE//BC)
\(\widehat{FIE}=\widehat{BIC}\)(hai góc đối đỉnh)
Do đó: ΔIFE~ΔIBC
=>\(\dfrac{IF}{IB}=\dfrac{IE}{IC}=\dfrac{FE}{BC}\)
=>\(\dfrac{IF}{IB}=\dfrac{4.8}{8}=\dfrac{3}{5}\)
c: Xét ΔIFC và ΔIBA có
\(\widehat{IFC}=\widehat{IBA}\)(hai góc so le trong, FC//BA)
\(\widehat{FIC}=\widehat{BIA}\)(hai góc đối đỉnh)
Do đó: ΔIFC~ΔIBA
=>\(\dfrac{IF}{IB}=\dfrac{IC}{IA}\)
=>\(\dfrac{IC}{IA}=\dfrac{IE}{IC}\)
=>\(IC^2=IE\cdot IA\)

Gọi độ dài của quãng đường AB là: \(x\left(km\right)\)
ĐK: \(x>0\)
Tổng vận tốc khi đi và về là: \(2\cdot40=80\left(km\right)\)
Vận tốc về là: \(\left(80+5\right):2=\dfrac{85}{2}\left(km/h\right)\)
Vận tốc đi là: \(\left(80-5\right):2=\dfrac{75}{2}\left(km/h\right)\)
Thời gian về là: \(x:\dfrac{85}{2}=\dfrac{2x}{85}\left(h\right)\)
Thời gian đi là: \(x:\dfrac{75}{2}=\dfrac{2x}{75}\left(h\right)\)
Thời gian về ít hơn thời gian đi 40p nên ta có pt:
\(\dfrac{2x}{75}-\dfrac{2x}{85}=\dfrac{40}{60}\)
\(\Leftrightarrow\dfrac{34x}{1275}-\dfrac{30x}{1275}=\dfrac{850}{1275}\)
\(\Leftrightarrow34x-30x=850\)
\(\Leftrightarrow4x=850\)
\(\Leftrightarrow x=\dfrac{425}{2}\left(tm\right)\)
Vậy: ....
Gọi x (km) là độ dài quãng đường AB (x > 0)
Thời gian đi từ A đến B: x/40 (h)
Thời gian đi từ B về A: x/45 (h)
40 phút = 2/3 h
Theo đề bài ta có phương trình:
x/40 - x/45 = 2/3
9x - 8x = 240
x = 240 (nhận)
Vậy quãng đường AB dài 240 km

Gọi diện tích rừng phải trồng theo kế hoạch là x(ha)
(ĐIều kiện: x>0)
Diện tích rừng trồng được trong thực tế là x+5(ha)
Thời gian dự kiến hoàn thành công việc là \(\dfrac{x}{15}\left(ngày\right)\)
Thời gian thực tế hoàn thành công việc là \(\dfrac{x+5}{20}\left(ngày\right)\)
Vì công việc hoàn thành trước 1 tuần=7 ngày nên ta có:
\(\dfrac{x}{15}-\dfrac{x+5}{20}=7\)
=>\(\dfrac{4x-3\left(x+5\right)}{60}=7\)
=>4x-3(x+5)=420
=>x-15=420
=>x=435(nhận)
Vậy: Diện tích rừng phải trồng là 435ha

Bài 2:
a; 10\(x\) - 12 = 3\(x\) + 6 + \(x\)
10\(x\) - 3\(x\) - \(x\) = 12 + 6
6\(x\) = 18
\(x\) = 18: 6
\(x\) = 3
Vậy \(x\) = 3
b; \(\dfrac{x-2}{4}\) - \(\dfrac{x}{12}\) = \(\dfrac{x-1}{6}\) - \(\dfrac{1}{3}\)
3.(\(x-2\)) - \(x\) = 2.(\(x-1\)) - 4
3\(x\) - 6 - \(x\) = 2\(x\) - 2 - 4
3\(x\) - \(x\) - 2\(x\) = 6 - 2 - 4
0 \(\times\) \(x\) = 0 \(\forall\) \(x\)
vậy \(x\) \(\in\) R
c; (\(x+1\))(2\(x\) - 3) = (2\(x\) - 1).(\(x+5\))
2\(x^2\) - 3\(x\) + 2\(x\) - 3 = 2\(x^2\) + 10\(x\) - \(x\) - 5
2\(x^2\) - 3\(x\) + 2\(x\) - 3 - 2\(x^2\) - 10\(x\) + \(x\) + 5 = 0
(2\(x^2\) - 2\(x^2\)) + (- 3\(x\) + 2\(x\) - 10\(x\) + \(x\)) + (5 - 3) = 0
0 - 10\(x\) + 2 = 0
10\(x\) = 2
\(x\) = \(\dfrac{2}{10}\)
\(x=\dfrac{1}{5}\)
Vậy \(x=\dfrac{1}{5}\)

a: \(A=\dfrac{x}{x-1}+\dfrac{2x}{1-x^2}-\dfrac{1}{x+1}\)
\(=\dfrac{x}{x-1}-\dfrac{2x}{\left(x-1\right)\left(x+1\right)}-\dfrac{1}{x+1}\)
\(=\dfrac{x\left(x+1\right)-2x-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x^2+x-3x+1}{\left(x-1\right)\left(x+1\right)}=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x-1}{x+1}\)
b: |x-1|=2
=>\(\left[{}\begin{matrix}x-1=2\\x-1=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
Khi x=3 thì \(A=\dfrac{3-1}{3+1}=\dfrac{2}{4}=\dfrac{1}{2}\)
c: Để A là số nguyên thì \(x-1⋮x+1\)
=>\(x+1-2⋮x+1\)
=>\(-2⋮x+1\)
=>\(x+1\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{0;-2;1;-3\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{0;-2;-3\right\}\)

Gọi tử số ban đầu là x
(ĐK: x<>-5)
Mẫu số ban đầu là x+5
Khi tăng cả tử và mẫu thêm 5 đơn vị thì được phân số mới là 2/3 nên ta có:
\(\dfrac{x+5}{x+5+5}=\dfrac{2}{3}\)
=>\(\dfrac{x+5}{x+10}=\dfrac{2}{3}\)
=>\(3\left(x+5\right)=2\left(x+10\right)\)
=>\(3x+15=2x+20\)
=>3x-2x=20-15
=>x=5(nhận)
mẫu số ban đầu là 5+5=10
vậy: Phân số ban đầu là \(\dfrac{5}{10}\)

Gọi số sách ban đầu ở thư viện thứ nhất là x(quyển)
(Điều kiện: \(x\in Z^+\))
Số sách ban đầu ở thư viện thứ hai là 20000-x(quyển)
Số sách lúc sau ở thư viện thứ nhất là x-2000(cuốn)
Số sách lúc sau ở thư viện thứ hai là 20000-x+2000=22000-x(cuốn)
Theo đề, ta có phương trình:
x-2000=22000-x
=>2x=24000
=>x=12000(nhận)
Vậy: Thư viện thứ nhất có 12000 cuốn, thư viện thứ hai có 20000-12000=8000 cuốn
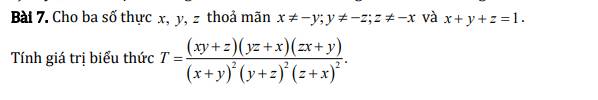




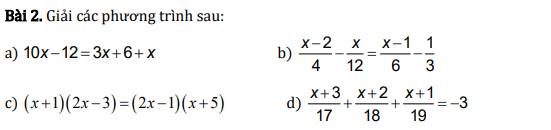

Lời giải:
Áp dụng BĐT Bunhiacopxky:
$(x^2+1)[1+(y+z)^2]\geq (x+y+z)^2$
$\Rightarrow \frac{3}{4}(x^2+1)[1+(y+z)^2]\geq \frac{3}{4}(x+y+z)^2$
Giờ ta chỉ cần cm:
$(y^2+1)(z^2+1)\geq \frac{3}{4}[1+(y+z)^2]$
$\Leftrightarrow 4(y^2z^2+y^2+z^2+1)\geq 3(y^2+z^2+2yz+1)$
$\Leftrightarrow 4y^2z^2+1+y^2+z^2-6yz\geq 0$
$\Leftrightarrow (2yz-1)^2+(y-z)^2\geq 0$ (luôn đúng)
Do đó ta có đpcm
Áp dụng BĐT Bunhiacopxky:
(�2+1)[1+(�+�)2]≥(�+�+�)2(x2+1)[1+(y+z)2]≥(x+y+z)2
⇒34(�2+1)[1+(�+�)2]≥34(�+�+�)2⇒43(x2+1)[1+(y+z)2]≥43(x+y+z)2
Giờ ta chỉ cần cm:
(�2+1)(�2+1)≥34[1+(�+�)2](y2+1)(z2+1)≥43[1+(y+z)2]
⇔4(�2�2+�2+�2+1)≥3(�2+�2+2��+1)⇔4(y2z2+y2+z2+1)≥3(y2+z2+2yz+1)
⇔4�2�2+1+�2+�2−6��≥0⇔4y2z2+1+y2+z2−6yz≥0
⇔(2��−1)2+(�−�)2≥0⇔(2yz−1)2+(y−z)2≥0 (luôn đúng)
Do đó ta có điều phải chứng minh