\(f\left(\dfrac{1}{x}\right)=a\left(\dfrac{1}{x}\right)^5+b\left(\dfrac{1}{x}\right)^3+b\left(\dfrac{1}{x}\right)^2+a\)

\(=\dfrac{a}{x^5}+\dfrac{b}{x^3}+\dfrac{b}{x^2}+a\)

\(=\dfrac{a+bx^2+bx^3+ax^5}{x^5}\)

\(=\dfrac{f\left(x\right)}{x^5}\)

\(\Rightarrow f\left(\dfrac{1}{2021}\right)=\dfrac{f\left(2021\right)}{2021^5}=\dfrac{2021}{2021^5}=\dfrac{1}{2021^4}\)

Diện tích mảnh đất là \(\left(3x+2\right)\left(2x+4\right)\left(m^2\right)\)

Diện tích phần đất trồng hoa là \(x\left(x+1\right)\left(m^2\right)\)

Diện tích phần đất còn lại là:

\(\left(3x+2\right)\left(2x+4\right)-x\left(x+1\right)\)

\(=6x^2+12x+4x+8-x^2-x\)

\(=5x^2+15x+8\left(m^2\right)\)

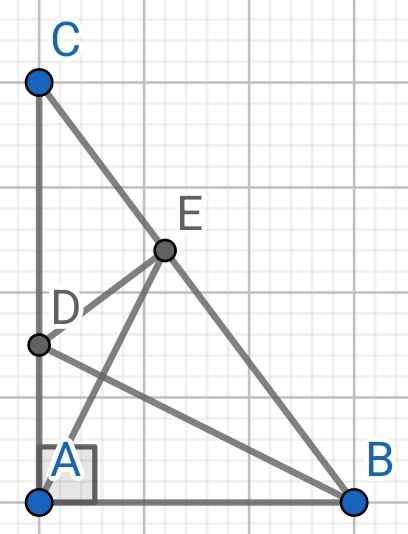
a) ∆ABC vuông tại A (gt)

⇒ BC là cạnh huyền nên là cạnh lớn nhất

b) Do BD là tia phân giác của ∠ABC (gt)

⇒ ∠ABD = ∠CBD

⇒ ∠ABD = ∠EBD

Xét ∆ABD và ∆EBD có:

BA = BE (gt)

∠ABD = ∠EBD (cmt)

BD là cạnh chung

⇒ ∆ABD = ∆EBD (c-g-c)

⇒ AD = ED (hai cạnh tương ứng)

a) ∆ABC vuông tại A (gt)

⇒ BC là cạnh huyền nên là cạnh lớn nhất

b) Do BD là tia phân giác của ∠ABC (gt)

⇒ ∠ABD = ∠CBD

⇒ ∠ABD = ∠EBD

Xét ∆ABD và ∆EBD có:

BA = BE (gt)

∠ABD = ∠EBD (cmt)

BD là cạnh chung

⇒ ∆ABD = ∆EBD (c-g-c)

⇒ AD = ED (hai cạnh tương ứng)

c) Sửa đề: AD < DC

Do AD = ED (cmt)

⇒ D nằm trên đường trung trực của AE (1)

Do BA = BE (gt)

⇒ B nằm trên đường trung trực của AE (2)

Từ (1) và (2) ⇒ BD là đường trung trực của AE

Do ∆ABD = ∆EBD (cmt)

⇒ ∠BAD = ∠BED (hai góc tương ứng)

⇒ ∠BED = 90⁰

⇒ ∠CED = 90⁰

⇒ ∆CED vuông tại E

⇒ DC là cạnh huyền nên là cạnh lớn nhất

⇒ ED < DC

Mà ED = AD (cmt)

⇒ AD < DC

$C=x^{2018}+|y+3|+\sqrt{\frac{3}{5}z-1}$
Ta thấy:

$x^{2018}\geq 0$ với mọi $x$

$|y+3|\geq 0$ với mọi $y$

$\sqrt{\frac{3}{5}z-1}\geq 0$ với mọi $z\geq \frac{5}{3}$
$\Rightarrow C\geq 0+0+0=0$ 

Vậy $C_{\min}=0$

Giá trị này đạt tại $x=|y+3|=\frac{3}{5}z-1=0$

$\Leftrightarrow x=0; y=-3; z=\frac{5}{3}$

$D=5-\sqrt{x^2+1}$
Vì $x^2\geq 0$ với mọi $x$

$\Rightarrow x^2+1\geq 1$

$\Rightarrow \sqrt{x^2+1}\geq 1$

$\Rightarrow D=5-\sqrt{x^2+1}\leq 5-1=4$
Vậy $D_{\max}=4$. Giá trị này đạt tại $x^2=0\Leftrightarrow x=0$

\(-\dfrac{8}{9};\dfrac{40}{-45};\dfrac{-32}{36}\)

rồi bài đâu?

Bài đâu bn ?????????

Để giải phương trình (x+3)^2 = (x+3)(x-3), bạn có thể làm như sau:

1. Mở ngoặc trái phải của phần bên phải (x+3)(x-3):
   (x+3)^2 = x^2 - 3x + 3x - 9

2. Rút gọn các thành phần:
   (x+3)^2 = x^2 - 9

3. Khi đó, phương trình trở thành:
   x^2 + 6x + 9 = x^2 - 9

4. Loại bỏ x^2 ở hai bên:
   6x + 9 = -9

5. Trừ 9 từ hai bên:
   6x = -9 - 9

6. Tổng hợp các thành phần:
   6x = -18

7. Chia hai bên cho 6 để giải x:
   x = -18/6
   x = -3

Vậy giá trị của x là -3.

\(\left(x+3\right)^2=\left(x+3\right)\left(x-3\right)\)

\(\Leftrightarrow\left(x+3\right)^2-\left(x+3\right)\left(x-3\right)=0\)

\(\Leftrightarrow\left(x+3\right)\left[\left(x+3\right)-\left(x-3\right)\right]=0\)

\(\Leftrightarrow\left(x+3\right).6=0\)

\(\Leftrightarrow x+3=0\)

\(\Leftrightarrow x=-3\)

a: Sửa đề: Chứng minh AM\(\perp\)BC

  ΔBAC cân tại A

mà AM là đường trung tuyến

nên AM\(\perp\)BC

b: Xét ΔABM và ΔACM có

AB=AC

BM=CM

AM chung

Do đó: ΔABM=ΔACM

Em đăng đề lên nhé