Tìm x,
y,z 3x=4y=5z và x-(y+z)=-21
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,M\left(x\right)=A\left(x\right)-2\cdot B\left(x\right)+C\left(x\right)\\ =\left(2x^5-4x^3+x^2-2x+2\right)-2\left(x^5-2x^4+x^2-5x+2\right)+\left(x^4+4x^3+3x^2-8x+2\dfrac{3}{4}\right)\\ =2x^5-4x^3+x^2-2x+2-2x^5+4x^4-2x^2+10x-4+x^4+4x^3+3x^2-8x+2,75\\ =\left(2x^5-2x^5\right)+\left(4x^4+x^4\right)+\left(-4x^3+4x^3\right)+\left(x^2-2x^2+3x^2\right)+\left(-2x+10x-8x\right)+\left(2-4+2,75\right)\\ =5x^4+2x^2+0,75\)
b, Thay x = -√0,25 = -0,5 vào M(x)
\(M\left(-0,5\right)=5\cdot\left(-0,5\right)^4+2\cdot\left(-0,5\right)^2+0,75\\ =0,3125+0,5+0,75\\ =1,5625\)
c, Vì \(5x^4\ge0;2x^2\ge0=>M\left(x\right)\ge0,75\)
Vậy không có giá trị nào của x để M(x) = 0


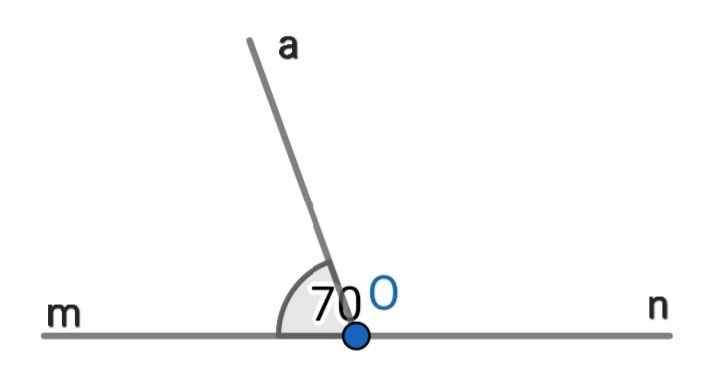 mOn là góc bẹt nên mOn = 180⁰
mOn là góc bẹt nên mOn = 180⁰
Thầy nghĩ là em ghi sai đề cả 2 câu a và b.
Em xem lại đề nhé!

Bài 5:
x-y-3=0
=>x-y=3
\(M=x^3-x^2y-3x^2+xy-y^2-4y+x+2021\)
\(=x^2\left(x-y\right)-3x^2+y\left(x-y\right)-4y+x+2021\)
\(=3x^2-3x^2+3y-4y+x+2021\)
=x-y+2021
=3+2021
=2024
Bài 4:
x=2999 nên x+1=3000
\(F\left(x\right)=x^{99}-3000x^{98}+3000x^{97}-...+3000x-1\)
\(=x^{99}-x^{98}\left(x+1\right)+x^{97}\left(x+1\right)-...+x\left(x+1\right)-1\)
\(=x^{99}-x^{99}-x^{98}+x^{98}+x^{97}-...+x^2+x-1\)
=x-1
=2998
Bài 3:
a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
BA=BD
Do đó: ΔBAM=ΔBDM
=>MA=MD
Xét ΔMAN vuông tại A và ΔMDC vuông tại D có
MA=MD
\(\widehat{AMN}=\widehat{DMC}\)(hai góc đối đỉnh)
Do đó: ΔMAN=ΔMDC
=>MN=MC
=>ΔMNC cân tại M
b: Ta có: ΔMAN=ΔMDC
=>AN=DC
Ta có: BA+AN=BN
BD+DC=BC
mà BA=BD và AN=DC
nên BN=BC
=>B nằm trên đường trung trực của NC(1)
Ta có: MN=MC
=>M nằm trên đường trung trực của NC(2)
Ta có: IN=IC
=>I nằm trên đường trung trực của NC(3)
Từ (1),(2),(3) suy ra B,M,I thẳng hàng

-1,5 < 2,5 nha bạn
-1,5 là số âm trong khi 2,5 là số dương hiển nhiên -1,5 < 0 < 2,5 rồi nhé bạn
3x=4y=5z
=>\(\dfrac{3x}{60}=\dfrac{4y}{60}=\dfrac{5z}{60}\)
=>\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{12}\)
mà x-y-z=-21
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{12}=\dfrac{x-y-z}{20-15-12}=\dfrac{-21}{-7}=3\)
=>\(x=3\cdot20=60;y=15\cdot3=45;z=12\cdot3=36\)