Biết độ dài ba cạnh của một tam giác tỉ lệ thuận với 3; 4; 5 và tổng độ dài cạnh lớn nhất và cạnh nhỏ nhất bằng 40m. Tính độ dài ba cạnh của tam giác đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Giải:
a; Khi rút ngẫu nhiên một tấm thẻ từ hộp chứa 8 tấm thẻ thì có 8 khả năng có thể xảy ra.
Xét các số 2; 3; 4; 5; 6; 7; 8; 9
Vì các số lẻ thuộc dãy số trên lần lượt là: 3; 5; 7; 9 (có 4 số lẻ)
Nên có 4 kết quả thuận lợi cho biến cố lấy được thẻ là số lẻ.
vậy xác suất của biến cố lấy được thẻ số lẻ là: 4 : 8 = \(\dfrac{1}{2}\)
b; Xét các số 2; 3; 4; 5; 6; 7; 8; 9
Vì các số chẵn thuộc dãy số trên lần lượt là: 2; 4; 6; 8 (có 4 số chẵn)
Nên có 4 kết quả thuận lợi cho biến cố lấy được thẻ là số chẵn.
Vậy xác suất của biến cố lấy được thẻ số chẵn là: 4 : 8 = \(\dfrac{1}{2}\)
c; Xét các số 2; 3; 4; 5; 6; 7; 8; 9
Vì các số nguyên tố thuộc dãy số trên lần lượt là các số: 2; 3; 5; 7 (có 4 số nguyên tố)
Nên có 4 kết quả thuận lợi cho biến cố lấy được thẻ là số chẵn.
Vậy xác suất của biến cố lấy được thẻ số nguyên tố là: 4 : 8 = \(\dfrac{1}{2}\)
Kết luận: a; Xác suất của biến cố lấy được thẻ số lẻ là \(\dfrac{1}{2}\)
b; Xác suất của biến cố lấy được thẻ là số chẵn là \(\dfrac{1}{2}\)
c; Xác suất của biến cố lấy được thẻ là số nguyên tố là \(\dfrac{1}{2}\)
a) Có 4 khả năng lấy được số lẻ là: 3; 5; 7; 9
Xác suất của biến cố "lấy được thẻ ghi số lẻ":
\(P=\dfrac{4}{8}=\dfrac{1}{2}\)
b) Có 4 khả năng lấy được thẻ ghi số chẵn là: 2; 4; 6; 8
Xác suất của biến cố "lấy được thẻ ghi số chẵn":
\(P=\dfrac{4}{8}=\dfrac{1}{2}\)
c) Có 4 thẻ ghi số nguyên tố là: 2; 3; 5; 7
Xác suất của biến cố "lấy được thẻ ghi số nguyên tố":
\(P=\dfrac{4}{8}=\dfrac{1}{2}\)

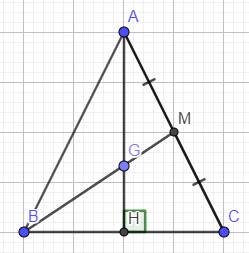
a) Do \(\Delta ABC\) cân tại A (gt)
\(\Rightarrow AB=AC\)
Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta AHC\) có:
\(AH\) là cạnh chung
\(AB=AC\left(cmt\right)\)
\(\Rightarrow\Delta AHB=\Delta AHC\) (cạnh huyền - cạnh góc vuông)
b) \(\Delta ABC\) cân tại A (gt)
\(AH\) là đường cao (gt)
\(\Rightarrow AH\) là đường trung tuyến của \(\Delta ABC\)
c) Do \(AH\) là đường trung tuyến của \(\Delta ABC\)
\(G\in AH\) (gt)
\(AG=2GH\left(gt\right)\)
\(\Rightarrow G\) là trọng tâm của \(\Delta ABC\)
Lại có:
\(M\) là trung điểm của \(AC\left(gt\right)\)
\(\Rightarrow BM\) là đường trung tuyến của \(\Delta ABC\)
Mà \(G\) là trọng tâm của \(\Delta ABC\)
\(\Rightarrow B,G,M\) thẳng hàng

B = \(\dfrac{1}{\left(2x-3\right)^2+5}\)
(2\(x-3\))2 ≥ 0 ∀ \(x\)
(2\(x\) - 3)2 + 5 ≥ 0 + 5 = 5 ∀ \(x\)
⇒ B = \(\dfrac{1}{\left(2x-3\right)^2+5}\) ≤ \(\dfrac{1}{5}\) ∀ \(x\)
Bmax = \(\dfrac{1}{5}\) ⇔ (2\(x\) - 3)2 = 0⇒ \(x=\dfrac{3}{2}\)
Kết luận giá trị lớn nhất của B là \(\dfrac{1}{5}\) xảy ra khi \(x=\dfrac{3}{2}\)
\(B=\dfrac{1}{\left(2x-3\right)^2+5}\)
Ta có:
\(\left(2x-3\right)^2\ge0\) với mọi \(x\in R\)
\(\Rightarrow\left(2x-3\right)^2+5\ge5\) với mọi \(x\in R\)
\(\Rightarrow\dfrac{1}{\left(2x-3\right)^2+5}\le\dfrac{1}{5}\) với mọi \(x\in R\)
\(\Rightarrow maxB=\dfrac{1}{5}\) khi \(2x-3=0\Leftrightarrow x=\dfrac{3}{2}\)


Tìm nghiệm của các đa thức sau:
c. \(x^2\) + 6\(x\) - 7
Nghiệm của đa thức là giá trị của \(x\) để đa thức bằng 0 nên ta có:
\(x^2\) - \(x\) + 7\(x\) - 7 = 0
(\(x^2\) - \(x\)) + (7\(x\) - 7) = 0
\(x\)(\(x\) - 1) + 7.(\(x-1\)) = 0
(\(x-1\)).(\(x+7\)) = 0
\(\left[{}\begin{matrix}x-1=0\\x+7=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=1\\x=-7\end{matrix}\right.\)
Vậy nghiệm của đa thức đã cho là:
\(x\in\) {1; - 7}
g; C(\(x\)) = \(\dfrac{1}{2}\) - 7\(x\) + 2\(x^3\) - 2.(\(x+2^3\) + \(x^3\))
Nghiệm của đa thức C(\(x\)) là giá trị của \(x\) để C(\(x\)) = 0 nên ta có phương trình:
\(\dfrac{1}{2}\) - 7\(x\) + 2\(x^3\) - 2.(\(x\) + 23 + \(x^3\)) = 0
\(\dfrac{1}{2}\) - 7\(x\) + 2\(x^{3^{ }}\) - 2\(x\) - 16 - 2\(x^3\) = 0
(\(\dfrac{1}{2}\) - 16) - (7\(x\) + 2\(x\)) + (2\(x^3\) - 2\(x^3\)) = 0
\(\dfrac{-31}{2}\) - 9\(x\) + 0 = 0
- \(\dfrac{31}{2}\) - 9\(x\) = 0
9\(x\) = - \(\dfrac{31}{2}\)
\(x\) = - \(\dfrac{31}{2}\) : 9
\(x\) = - \(\dfrac{31}{18}\)
Vậy \(x=-\dfrac{31}{18}\)

Nó còn phụ thuộc vào điểm các đợt kiểm tra của kì II mới tính được điểm tổng kết cả năm môn toán em nhé.
khả năng 80% là chị ko lên lớp dc, vì em nghe nói cấp 2 điểm trung bình tất cả các môn là 5

Đây là toán nâng cao chuyên đề toán xác suất thống kê, cấu trúc thi chuyên, thi học sinh giỏi các cấp, thi violympic. Hôm nay Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
+ Khi gieo một con xúc xắc cân đối và đồng chất liên tiếp 2 lần, thì có thể có các khả năng sau xảy ra:
Trường hợp 1: sấp; sấp
Trường hợp 2: sấp; ngửa
Trường hợp 3: ngửa; sấp
Trường hợp 4: ngửa ngửa
+ Vậy khi gieo một con xúc xắc cân đối và đồng chất thì có bốn khả năng xảy ra.
Trong đó có một kết quả thuận lợi cho việc hai lần gieo đồng xu đều xuất hiện mặt ngửa.
+ Từ những lập luận trên ta có xác suất của biến cố hai lần gieo đồng xu đều xuất hiện mặt ngửa là:
1 : 4 = \(\dfrac{1}{4}\)
Chọn C. \(\dfrac{1}{4}\)

a: Xét ΔABC có AB<AC<BC
mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: Xét ΔCDB có
CA,DK là các đường trung tuyến
CA cắt DK tại M
Do đó: M là trọng tâm của ΔCDB
=>\(CM=\dfrac{2}{3}CA=\dfrac{2}{3}\cdot4=\dfrac{8}{3}\left(cm\right)\)
c: Gọi I là trung điểm của AC
d là trung trực của AC
mà I là trung điểm của AC
nên IQ\(\perp\)AC tại I
=>IQ//AD
Xét ΔCAD có
I là trung điểm của AC
IQ//AD
Do đó: Q là trung điểm của CD
Xét ΔCDB có
M là trọng tâm
Q là trung điểm của CD
Do đó: B,M,Q thẳng hàng




Gọi a (m), b (m), c (m) lần lượt là độ dài ba cạnh của tam giác (a, b, c > 0)
Do độ dài ba cạnh tỉ lệ thuận với 3; 4; 5 nên:
a/3 = b/4 = c/5
Do tổng độ dài cạnh lớn nhất và cạnh nhỏ nhất là 40 m nên:
a + c = 40
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a/3 = b/4 = c/5 = (a + c)/(3 + 5) = 40/8 = 5
a/3 = 5 ⇒ a = 5.3 = 15 (nhận)
b/4 = 5 ⇒ b = 5.4 = 20 (nhận)
c/5 = 5 ⇒ c = 5.5 = 25 (nhận)
Vậy độ dài ba cạnh của tam giâc cần tìm là: 15 m, 20 m, 25 m