Cho tam giác ABC vuông tại A, BD là tia phân giác của góc ABC( D thuộc AC). Kẻ DE vuông góc với BC tại E. a) CM tam giác ABD bằng tam giác EBD. b) Kẻ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm I sao cho HA=HI chứng minh EI= EA. c) Gọi M là giao điểm của BD và AE, IM cắt BC tại F chứng minh F là trọng tâm của tam giác AIE. d) CM MF<ME.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(B=\dfrac{1}{4\cdot9}+\dfrac{1}{9\cdot14}+...+\dfrac{1}{44\cdot49}\)
\(=\dfrac{1}{5}\left(\dfrac{5}{4\cdot9}+\dfrac{5}{9\cdot14}+...+\dfrac{5}{44\cdot49}\right)\)
\(=\dfrac{1}{5}\left(\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{14}+...+\dfrac{1}{44}-\dfrac{1}{49}\right)\)
\(=\dfrac{1}{5}\left(\dfrac{1}{4}-\dfrac{1}{49}\right)=\dfrac{1}{5}\cdot\dfrac{45}{196}=\dfrac{9}{196}\)


a: ĐKXĐ: x<>1
Để E là số nguyên thì \(3-x⋮x-1\)
=>\(x-3⋮x-1\)
=>\(x-1-2⋮x-1\)
=>\(-2⋮x-1\)
=>\(x-1\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{2;0;3;-1\right\}\)
b: \(E=\dfrac{3-x}{x-1}=\dfrac{-\left(x-3\right)}{x-1}=\dfrac{-\left(x-1-2\right)}{x-1}=-1+\dfrac{2}{x-1}\)
Để E min thì x-1=-1
=>x=0

ĐKXĐ: \(x>=\dfrac{5}{6}\)
\(4\sqrt{\dfrac{x}{5}-\dfrac{1}{6}}>=0\forall x\) thỏa mãn ĐKXĐ
=>\(-4\sqrt{\dfrac{x}{5}-\dfrac{1}{6}}< =0\forall x\) thỏa mãn ĐKXĐ
=>\(B=-4\sqrt{\dfrac{x}{5}-\dfrac{1}{6}}+\dfrac{1}{12}< =\dfrac{1}{12}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi \(\dfrac{x}{5}-\dfrac{1}{6}=0\)
=>\(\dfrac{x}{5}=\dfrac{1}{6}\)
=>\(x=\dfrac{5}{6}\)

Em phải viết số theo đúng với đề bài thì mới biết vị trí của que diêm để di chuyển chứ em?

B = - \(\dfrac{5}{2}\) - \(\dfrac{2}{3}\) \(\sqrt{\dfrac{x}{2}+3}\)
B = - (\(\dfrac{5}{2}\) + \(\dfrac{2}{3}\)\(\sqrt{\dfrac{x}{2}+3}\)) (đk \(\dfrac{x}{2}\) + 3 ≥ 0 ⇒ \(x\) ≥ - 6)
\(\sqrt{\dfrac{x}{2}+3}\) ≥ 0
⇒ \(\dfrac{2}{3}\)\(\sqrt{\dfrac{x}{2}+3}\) ≥ 0
⇒ \(\dfrac{5}{2}+\dfrac{2}{3}\sqrt{\dfrac{x}{2}+3}\) ≥ \(\dfrac{5}{2}\)
⇒ -(\(\dfrac{5}{2}\) + \(\dfrac{2}{3}\)\(\sqrt{\dfrac{x}{2}+3}\)) ≤ - \(\dfrac{5}{2}\)
Vậy Bmax = - \(\dfrac{5}{2}\) khi \(\sqrt{\dfrac{x}{2}+3}\) = 0 ⇒ \(\dfrac{x}{2}\) + 3 = 0 ⇒ \(\dfrac{x}{2}\) = -3; ⇒ \(x=-6\)
Kết luận: Giá trị lớn nhất của biểu thức là - \(\dfrac{5}{2}\) xảy ra khi \(x=-6\)

Sửa đề: cắt BC lần lượt tại E và F
a: Ta có: E nằm trên đường trung trực của AB
=>EA=EB
=>ΔEAB cân tại E
b: D nằm trên đường trung trực của AC
=>DA=DC
F nằm trên đường trung trực của AC
=>FC=FA
Xét ΔADF và ΔCDF có
DA=DC
DF chung
FA=FC
Do đó: ΔADF=ΔCDF

A B C D E F M N
a/ Xét tg ABE có
\(DM\perp AB\Rightarrow EM\perp AB\)
=> tg ABE cân tại E (Tam giác có đường cao đồng thời là đường trunbg trực thì tg đó là tg cân)
b/
Xét tg ACF, chứng minh tương tự câu a => tg ACF cân tại F
=> AF = CF (1)
Xét tg ACD, chứng minh tương tự => tg ACD cân tại D
=> AD = CD (2)
Xét tg ADF và tg CDF có
DF chung (3)
Từ (1) (2) (3) => tg ADF = tg CDF (c.c.c)
c/
Xét tg ABD, chứng minh tương tự câu a => tg ABD cân tại D
\(\Rightarrow\widehat{ABD}=\widehat{BAD}\)
Ta có tg ACD cân (cmt) \(\Rightarrow\widehat{CAD}=\widehat{ACD}\)
\(\Rightarrow\widehat{BAD}+\widehat{CAD}=\widehat{BAC}=120^o=\widehat{ABD}+\widehat{ACD}\)
Xét tứ giác ABDC có
\(\widehat{BDC}=360^o-\widehat{BAC}-\left(\widehat{ABD}+\widehat{ACD}\right)\) (Tổng các góc trong của 1 tứ giác bằng \(360^o\))
\(\Rightarrow\widehat{BDC}=360^o-120^o-120^o=120^o\)
Ta có
tg ABD cân tại D (cmt) => AD = BD
tg ACD cân tại D (cmt) => AD = CD
=> BD = CD => tg BCD cân tại D \(\Rightarrow\widehat{CBD}=\widehat{BCD}\) (4)
Xét tg cân BCD có
\(\widehat{CBD}+\widehat{BCD}=180^o-\widehat{BDC}=180^o-120^o=60^o\) (5)
Từ (4) và (5) \(\Rightarrow\widehat{CBD}=\widehat{BCD}=\dfrac{60^o}{2}=30^o\)
Chứng minh tương tự câu b => tg DE = tg BDE (c.c.c)
\(\Rightarrow\widehat{EAD}=\widehat{CBD}=30^o\)
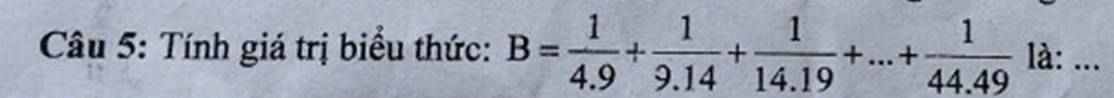

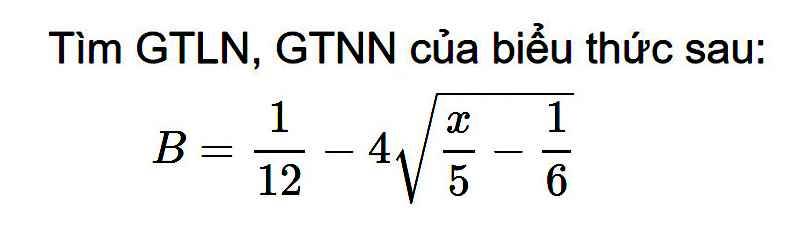
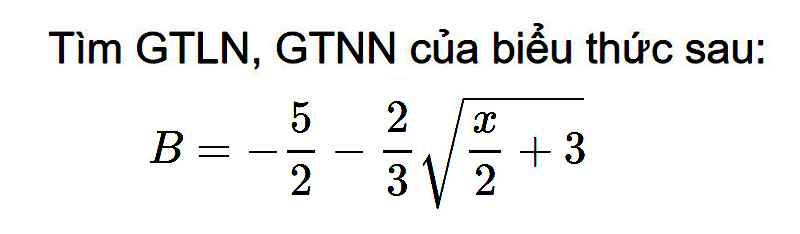
a) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠CBD
⇒ ∠ABD = ∠EBD
Xét hai tam giác vuông: ∆ABD và ∆EBD có:
BD chung
∠ABD = ∠EBD (cmt)
⇒ ∆ABD = ∆EBD (cạnh huyền - góc nhọn)
b) Do HA = HI (gt)
⇒ H là trung điểm của AI
Mà AH ⊥ BC tại H (gt)
⇒ AI ⊥ BC
⇒ BC là đường trung trực của AI
Mà E ∈ BC
⇒ EA = EI
c) Do ∆ABD = ∆EBD (cmt)
⇒ BA = BE (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AE (1)
Do ∆ABD = ∆EBD (cmt)
⇒ AD = ED (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AE (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AE
Mà M là giao điểm của BD và AE
⇒ M là trung điểm của AE
⇒ IM là đường trung tuyến của ∆AIE
Lại có:
H là trung điểm của AE (cmt)
⇒ EH là đường trung tuyến của ∆AIE
∆AIE có:
IM là đường trung tuyến (cmt)
EH là đường trung tuyến (cmt)
Mà IM cắt EH tại F
⇒ F là trọng tâm của ∆AIE
d) Do F là trọng tâm của ∆AIE (cmt)
⇒ HF < HE
⇒ AF < AE (quan hệ giữa đường xiên và hình chiếu)
Lại có:
F nằm trên đường trung trực của AI (do BC là đường trung trực của AI)
⇒ AF = IF
Do F là trọng tâm của ∆AIE (cmt)
⇒ IF = 2MF
Do M là trung điểm của AE (cmt)
⇒ AE = 2ME
Mà AF < AE (cmt)
⇒ AF < 2ME
Mà AF = IF (cmt)
⇒ IF < 2ME
Mà IF = 2MF (cmt)
⇒ 2MF < 2ME
⇒ MF < ME
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Xét ΔEHA vuông tại H và ΔEHI vuông tại H có
EH chung
HA=HI
Do đó: ΔEHA=ΔEHI
=>EA=EI
c: ΔBAD=ΔBED
=>BA=BE và DA=DE
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE tại M và M là trung điểm của AE
Xét ΔAEI có
EH,IM là các đường trung tuyến
EH cắt IM tại F
Do đó: F là trọng tâm của ΔAEI