a: Xét tứ giác MIKC có \(\widehat{MIC}=\widehat{MKC}=90^0\)

nên MIKC là tứ giác nội tiếp

Xét tứ giác MIAH có \(\widehat{MIA}+\widehat{MHA}=90^0+90^0=180^0\)

nên MIAH là tứ giác nội tiếp

Xét tứ giác MKBH có \(\widehat{MKB}+\widehat{MHB}=90^0+90^0=180^0\)

nên MKBH là tứ giác nội tiếp

b: Ta có: MIKC là tứ giác nội tiếp

=>\(\widehat{MIK}+\widehat{MCK}=180^0\)

=>\(\widehat{MIK}=180^0-\widehat{MCB}\)

Ta có: HAIM là tứ giác nội tiếp

=>\(\widehat{MIH}=\widehat{MAH}\)

mà \(\widehat{MAH}=\widehat{MCB}\left(=180^0-\widehat{MAB}\right)\)

nên \(\widehat{MIH}=\widehat{MCB}\)

=>\(\widehat{MIH}+\widehat{MIK}=180^0\)

=>K,I,H thẳng hàng

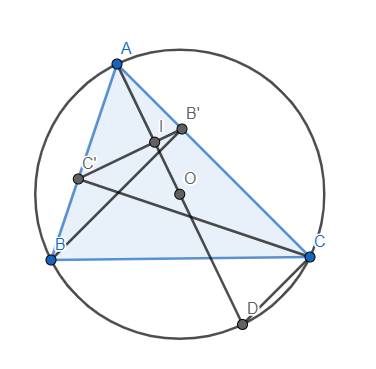
 a) Tứ giác BCB'C' có \(\widehat{BC'C}=\widehat{BB'C}=90^o\) nên nó là tứ giác nội tiếp (2 đỉnh kề nhau nhìn cạnh đối diện dưới 2 góc bằng nhau)

 b) Vì tứ giác BCB'C' nội tiếp nên \(\widehat{AB'C'}=\widehat{ABC}\) (góc ngoài bằng góc trong đối)

 Xét tam giác AB'C' và tam giác ABC có:

 \(\widehat{BAC}\) chung và \(\widehat{AB'C'}=\widehat{ABC}\)

 \(\Rightarrow\Delta AB'C'\sim\Delta ABC\left(g.g\right)\)

c) Theo câu b), ta có \(\widehat{AB'I}=\widehat{ABC}\)

Lại có \(\widehat{ABC}=\widehat{ADC}\) (góc nội tiếp cùng chắn cung AC)

\(\Rightarrow\widehat{AB'I}=\widehat{ADC}\) \(\Rightarrow\) Tứ giác B'IDC nội tiếp (góc ngoài bằng góc trong đối)

a: Xét tứ giác BC'B'C có \(\widehat{BC'C}=\widehat{BB'C}=90^0\)

nên BC'B'C là tứ giác nội tiếp

b: Ta có: BC'B'C là tứ giác nội tiếp

=>\(\widehat{BC'B'}+\widehat{BCB'}=180^0\)

mà \(\widehat{BC'B'}+\widehat{AC'B'}=180^0\)

nên \(\widehat{AC'B'}=\widehat{ACB}\)

Xét ΔAC'B' và ΔACB có

\(\widehat{AC'B'}=\widehat{ACB}\)

\(\widehat{CAB}\) chung

Do đó: ΔAC'B'~ΔACB

\(\sqrt{3+2\sqrt{2}}-\sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\)

\(=\sqrt{2+2\sqrt{2}+1}-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}}\)

\(=\sqrt{\left(\sqrt{2}\right)^2+2\sqrt{2}\cdot1+1^2}-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}}\)

\(=\sqrt{\left(\sqrt{2}+1\right)^2}-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}\right)^2-1^2}}\)

\(=\sqrt{2}+1-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{2-1}}\)

\(=\sqrt{2}+1-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{1}}\)

\(=\sqrt{2}+1-\sqrt{\left(\sqrt{2}-1\right)^2}\)

\(=\sqrt{2}+1-\left(\sqrt{2}-1\right)\)

\(=\sqrt{2}+1-\sqrt{2}+1=2\)

Đk: \(x\ge0\)

pt đã cho \(\Leftrightarrow6\sqrt{2x+7}-\left(\dfrac{3}{2}x+\dfrac{33}{2}\right)=2\sqrt{x}-\left(\dfrac{1}{2}x+\dfrac{3}{2}\right)\)

\(\Leftrightarrow\dfrac{36\left(2x+7\right)-\left(\dfrac{3}{2}x+\dfrac{33}{2}\right)^2}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{4x-\left(\dfrac{1}{2}x+\dfrac{3}{2}\right)^2}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\)

\(\Leftrightarrow\dfrac{72x+252-\dfrac{9}{4}x^2-\dfrac{99}{2}x-\dfrac{1089}{4}}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{4x-\dfrac{1}{4}x^2-\dfrac{3}{2}x-\dfrac{9}{4}}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\)

\(\Leftrightarrow\dfrac{-\dfrac{9}{4}x^2+\dfrac{45}{2}x-\dfrac{81}{4}}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{-\dfrac{1}{4}x^2+\dfrac{5}{2}x-\dfrac{9}{4}}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\)

\(\Leftrightarrow\dfrac{x^2-10x+9}{-\dfrac{4}{9}\left(6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}\right)}=\dfrac{x^2-10x+9}{-4\left(2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}\right)}\)

\(\Leftrightarrow\left(x^2-10x+9\right)\left[\dfrac{9}{4\left(6+\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}\right)}-\dfrac{1}{4\left(2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}\right)}\right]=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-10x+9=0\\\dfrac{9}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{1}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\end{matrix}\right.\)

Với \(x^2-10x+9=0\Leftrightarrow\left(x-1\right)\left(x-9\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=9\end{matrix}\right.\) (nhận)

pt nhỏ thứ 2 \(\Leftrightarrow18\sqrt{x}+\dfrac{9}{2}x+\dfrac{27}{2}=6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}\)

\(\Leftrightarrow6\sqrt{2x+7}-18\sqrt{x}=3x-3\)

\(\Leftrightarrow2\sqrt{2x+7}-6\sqrt{x}=x-1\)

\(\Leftrightarrow\dfrac{4\left(2x+7\right)-36x}{2\sqrt{2x+7}+6\sqrt{x}}=x-1\)

\(\Leftrightarrow\dfrac{28-28x}{2\sqrt{2x+7}+6\sqrt{x}}=x-1\)

\(\Leftrightarrow\left(x-1\right)\left(1+\dfrac{28}{2\sqrt{2x+7}+6\sqrt{x}}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\1+\dfrac{28}{2\sqrt{2x+7}+6\sqrt{x}}=0\left(loại\right)\end{matrix}\right.\)

Vậy pt đã cho có tập nghiệm \(S=\left\{1;9\right\}\)

Bài III:

1: ĐKXĐ: y>=-1 và x<>y

\(\left\{{}\begin{matrix}\dfrac{2}{x-y}+\sqrt{y+1}=4\\\dfrac{1}{x-y}-3\sqrt{y+1}=-5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{6}{x-y}+3\sqrt{y+1}=12\\\dfrac{1}{x-y}-3\sqrt{y+1}=-5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{7}{x-y}=7\\\dfrac{1}{x-y}-3\sqrt{y+1}=-5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x-y=1\\3\sqrt{y+1}=1+5=6\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x-y=1\\y+1=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=3\\x=y+1=4\end{matrix}\right.\left(nhận\right)\)

2: 

a: Thay m=1 vào (d), ta được:

\(y=x\cdot1-2\cdot1+4=x+2\)

Phương trình hoành độ giao điểm là:

\(x^2=x+2\)

=>\(x^2-x-2=0\)

=>(x-2)(x+1)=0

=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)

Thay x=2 vào y=x+2, ta được:

y=2+2=4

Thay x=-1 vào y=x+2, ta được:

y=-1+2=1

Vậy: (d) cắt (P) tại A(2;4) và B(-1;1)

b: Phương trình hoành độ giao điểm là:

\(x^2=mx-2m+4\)

=>\(x^2-mx+2m-4=0\)

\(\text{Δ}=\left(-m\right)^2-4\cdot1\left(2m-4\right)\)

\(=m^2-8m+16=\left(m-4\right)^2\)

Để (d) cắt (P) tại hai điểm phân biệt thì Δ>0

=>(m-4)²>0

=>\(m-4\ne0\)

=>\(m\ne4\)

Theo Vi-et, ta được:

\(x_1+x_2=-\dfrac{b}{a}=m;x_1x_2=\dfrac{c}{a}=2m-4\)

\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)

\(=m^2-2\left(2m-4\right)\)

\(=m^2-4m+8=\left(m-2\right)^2+4>=4\forall m\)

Dấu '=' xảy ra khi m=2

Xét 2024 số:

\(a_1=2024\)

\(a_2=20242024\)

\(a_3=202420242024\)

...

\(a_{2024}=20242024...2024\) (2024 lần cụm "2024")

 Một số khi chia cho 2023 thì có 2023 số dư phân biệt là 0, 1, 2,..., 2023 

 \(\Rightarrow\) Theo nguyên lí Dirichlet tồn tại 2 số \(a_i,a_j\left(i\ne j,1\le i< j\le2024\right)\) trong số 2024 số kể trên có cùng số dư khi chia cho 2023. 

 \(\Rightarrow a_j-a_i⋮2023\)

 \(\Rightarrow20242024...2024-20242024...2024⋮2023\)

       (\(j\) cụm "2024)          (\(i\) cụm "2024)

 \(\Rightarrow20242024...2024000...00⋮2023\) 

   (\(j-i\) cụm "2024" và \(i\) chữ số 0)

 \(\Rightarrow20242024...2024.10^i⋮2023\) (*)

 Nhưng vì \(10^i=2^i.5^i\) và \(2023=7.17^2\) nên \(ƯCLN\left(10^i,2023\right)=1\)

 Từ đó (*) suy ra \(20242024...2024⋮2023\)

                          (\(j-i\) cụm 2024)

 Ta có đpcm.

Ta có: EF song song MN (cùng vuông góc AB)

D là trung điểm OA \(\Rightarrow AD=OD=\dfrac{R}{2}\)

Mà \(AC=OB=R\)

\(\Rightarrow AC+AD=OD+OB\Rightarrow DC=BD\)

Hay D là trung điểm BD

\(\Rightarrow EF\) là đường trung bình tam giác BMN

\(\Rightarrow MN=2EF\)

AB là đường kính và E thuộc đường tròn \(\Rightarrow\widehat{AEB}=90^0\) hay tam giác  ABE vuông tại E

Áp dụng hệ thức lượng trong tam giác vuông ABE với đường cao ED:

\(ED^2=AD.DB=AD\left(OD+OB\right)=\dfrac{R}{2}.\left(\dfrac{R}{2}+R\right)=\dfrac{3R^2}{4}\)

\(\Rightarrow ED=\dfrac{R\sqrt{3}}{2}\)

\(\Rightarrow EF=2ED=R\sqrt{3}\)

\(\Rightarrow MN=2EF=2R\sqrt{3}\)

Gọi G là giao điểm của EF và AB. Ta có:

AG = AD + DG = R + R/2 = 3R/2

Vì tam giác ABC vuông tại C nên ta có:

AC^2 + BC^2 = AB^2

R^2 + BC^2 = (2R)^2

BC = R√3

Ta có:

CG = BC - BC/2 = R√3 - R√3/2 = R√3/2

Vì tam giác CGE vuông tại G nên ta có:

GE = CG * tan(∠GCE) = CG * tan(∠CBE)

GE = R√3/2 * tan(∠CBE)

Vì EF vuông góc với AB nên tam giác BEG vuông tại G, ta có:

BG^2 + GE^2 = BE^2

(R/2)^2 + (R√3/2 * tan(∠CBE))^2 = R^2

R^2/4 + 3R^2/4 * tan^2(∠CBE) = R^2

tan^2(∠CBE) = 1/3

tan(∠CBE) = √(1/3)

sin(∠CBE) = 1/√3

MN = 2 * GM = 2 * GE * sin(∠CBE)

MN = 2 * R√3/2 * √(1/3) = R

Vậy độ dài đoạn thẳng MN là R.

Để giải phép tính này, trước hết chúng ta cần thực hiện phép chia trước, sau đó thực hiện phép cộng. Dưới đây là cách giải:

1. 5322,666744 : 5,333332 = 998
2. 17443,478 : 0,993 = 17569

Sau đó, ta thực hiện phép cộng:

998 + 17569 = 18567

Vậy kết quả của phép tính là 18567 viết dưới dạng hỗn số.

Còn phần phân số đâu bạn.
Hỗn số có hai phần là: Số nguyên đứng trước dấu gạch ngang và phân số.