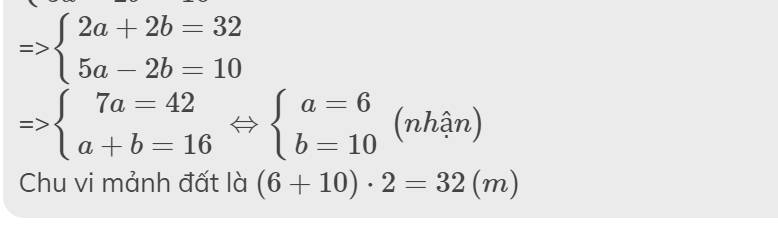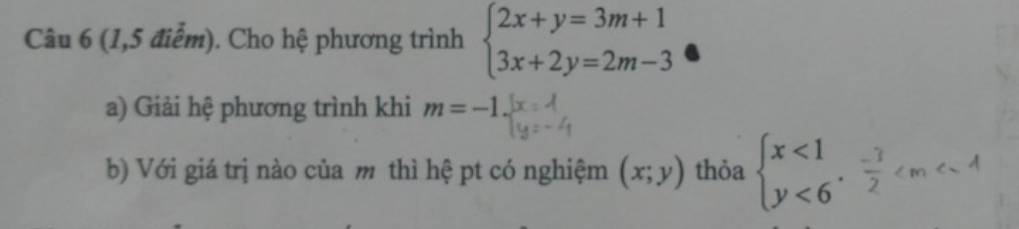Gọi chiều rộng và chiều dài của mảnh đất lần lượt là a(m) và b(m)

(Điều kiện: a>0 và b>0)

Nếu tăng mỗi chiều của mảnh đất thêm 4m thì diện tích tăng thêm 80m² nên ta có:

(a+4)(b+4)=ab+80

=>ab+4a+4b+16=ab+80

=>4a+4b=64

=>a+b=16(1)

Nếu giảm chiều rộng 2m và tăng chiều dài 5m thì diện tích mảnh đất không đổi nên ta có:

(a-2)(b+5)=ab

=>ab+5a-2b-10=ab

=>5a-2b=10(2)

Từ (1),(2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}a+b=16\\5a-2b=10\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2a+2b=32\\5a-2b=10\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}7a=42\\a+b=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=10\end{matrix}\right.\left(nhận\right)\)

Chu vi mảnh đất là \(\left(6+10\right)\cdot2=32\left(m\right)\)

Đặt: Độ dài chiều dài và rộng của mảnh vườn lần lượt là a và b (m; a>b>0)

=> Diện tích mảnh đất đó là ab (m²)

+) Nếu tăng mỗi chiều của mảnh đất đó thêm 4m thì diện tích mảnh đất đó tăng thêm 80m²

=> (a+4)(b+4)=ab+80 (m²)

=> ab+4a+4b+16=ab+80

=>4a+4b+16=80

=>4a+4b=64

=> 4(a+b)=64

=> a+b=16 (1)

+)Nếu giảm chiều rộng 2m và tăng chiều dài thêm 5m thì diện tích mảnh vườn không đổi

=> (a+5)(b-2)=ab(m²)

=>ab-2a+5b-10=ab

=>-2a+5b=10 (2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}a+b=16\Rightarrow2\left(a+b\right)=2a+2b=32\\-2a+5b=10\end{matrix}\right.\)

\(2a+2b-2a+5b=7b=42\)

\(b=6\)

Thay b = 6 vào (1)

=> a + 6 = 16

=> a = 10

Có a>b>0 (do 10>6>0)

=> tmđk: a = 10 và b = 6

=> Độ dài của chiều dài và rộng lần lượt là 10m và 6m

=> Chu vi mảnh vườn đó là: (10+6).2=32(m)

Đ/S: 32m

Xét ΔIMB vuông tại M và ΔINC vuông tại N có

\(\widehat{MIB}=\widehat{NIC}\)(hai góc đối đỉnh)

Do đó: ΔIMB~ΔINC

=>\(\dfrac{IM}{IN}=\dfrac{IB}{IC}\)

=>\(IM\cdot IC=IB\cdot IN\)

  Vận tốc này à bn :)

Gọi vận tốc lúc đầu của người đó là x(km/h)

(Điều kiện: x>0)

Thời gian dự kiến ban đầu là \(\dfrac{90}{x}\left(giờ\right)\)

1h9p=1,15h

Sau 1,15h, người đó đi được 1*x=x(km)

Độ dài quãng đường còn lại là 90-x(km)

Thời gian thực tế đi hết quãng đường là:

\(1,15+\dfrac{90-x}{x+4}\left(giờ\right)\)

Theo đề, ta có: 

\(\dfrac{90}{x}=1,15+\dfrac{90-x}{x+4}\)

=>\(\dfrac{90}{x}-\dfrac{90-x}{x+4}=1,15\)

=>\(\dfrac{90x+360-90x+x^2}{x\left(x+4\right)}=1,15\)

=>\(1,15\left(x^2+4x\right)=x^2+360\)

=>\(1,15x^2+4,6x-x^2-360=0\)

=>\(0,15x^2+4,6x-360=0\)

=>\(\left[{}\begin{matrix}x=36\left(nhận\right)\\x=-\dfrac{200}{3}\left(loại\right)\end{matrix}\right.\)

Vậy: Vận tốc lúc đầu của người đó là 36km/h

a.

Do MC, MD là các tiếp tuyến \(\Rightarrow\widehat{DMO}=\widehat{DNO}=90^0\)

\(\Rightarrow\)M và N cùng nhìn OD dưới 1 góc vuông nên DMON nội tiếp

b.

Xét hai tam giác MIA và NIM có:

\(\left\{{}\begin{matrix}\widehat{MIA}-chung\\\widehat{IMA}=\widehat{INM}\left(\text{cùng chắn MA}\right)\end{matrix}\right.\) 

\(\Rightarrow\Delta MIA\sim\Delta NIM\left(g.g\right)\)

\(\Rightarrow\dfrac{MI}{IN}=\dfrac{IA}{MI}\Rightarrow MI^2=IA.IN\)

c.

Theo t/c hai tiếp tuyến cắt nhau ta có \(DM=DN\)

Lại có \(OM=ON=R\)

\(\Rightarrow OD\) là trung trực MN

\(\Rightarrow OD\) vuông góc MN tại H

Xét hai tam giác OHM và OMD có:

\(\left\{{}\begin{matrix}\widehat{MOH}-chung\\\widehat{OHM}=\widehat{OMD}=90^0\end{matrix}\right.\)

\(\Rightarrow\Delta OHM\sim\Delta OMD\left(g.g\right)\)

\(\Rightarrow\dfrac{OH}{OM}=\dfrac{OM}{OD}\Rightarrow OM^2=OH.OD\)

\(\Rightarrow R^2=OH.\left(OH+HD\right)=3.\left(3+5\right)=24\)

\(\Rightarrow R=2\sqrt{6}\)

Chỉ cần giải câu C thôi cũng được ạ

Lời giải:

Ta có:

$\sin B = \frac{AH}{AB}\Rightarrow AB=\frac{AH}{\sin B}=\frac{3}{\frac{3}{4}}=4$

$\sin B=\frac{3}{4}\Rightarrow \widehat{B}=48,6^0$

$\widehat{C}=90^0-\widehat{B}=90^0-48,6^0=41,4^0$

a: Thay m=-1 vào hệ phương trình, ta được:

\(\left\{{}\begin{matrix}2x+y=3\cdot\left(-1\right)+1=-2\\3x+2y=2\cdot\left(-1\right)-3=-5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4x+2y=-4\\3x+2y=-5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4x+2y-3x-2y=-4+5\\2x+y=-2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=1\\y=-2-2x=-2-2=-4\end{matrix}\right.\)

b: Vì \(\dfrac{2}{3}\ne\dfrac{1}{2}\)

nên hệ luôn có nghiệm duy nhất

\(\left\{{}\begin{matrix}2x+y=3m+1\\3x+2y=2m-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4x+2y=6m+2\\3x+2y=2m-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x+y=3m+1\\4x+2y-3x-2y=6m+2-2m+3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=4m+5\\y=3m+1-2\left(4m+5\right)=3m+1-8m-10=-5m-9\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x< 1\\y< 6\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4m+5< 1\\-5m-9< 6\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4m< -4\\-5m< 15\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}m< -1\\m>-3\end{matrix}\right.\)

=>-3<m<-1

hpt \(\Leftrightarrow\left\{{}\begin{matrix}y=5-2x\\y+x^2=4x\end{matrix}\right.\) 

\(\Rightarrow5-2x+x^2=4x\)

\(\Leftrightarrow x^2-6x+5=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)

Nếu \(x=1\Rightarrow y=5-2x=3\)

Nếu \(x=5\Rightarrow y=5-2x=-5\) 

Vậy hpt đã cho có nghiệm \(\left(x;y\right)\in\left\{\left(1;3\right);\left(5;-5\right)\right\}\)

Bài 2:

Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)

nên ABOC là tứ giác nội tiếp

Bài 3:

a: Xét tứ giác MKHN có \(\widehat{MKN}=\widehat{MHN}=90^0\)

nên MKHN là tứ giác nội tiếp

b: Xét tứ giác PHIK có \(\widehat{PHI}+\widehat{PKI}=90^0+90^0=180^0\)

nên PHIK là tứ giác nội tiếp