
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 2x+6=0
=>2x=-6
=>x=-3
b: 4x+20=0
=>4x=-20
=>x=-5
c: 2(x+1)=5x-7
=>5x-7=2x+2
=>3x=9
=>x=3
d: \(2x-3=0\)
=>2x=3
=>\(x=\dfrac{3}{2}\)
e: 3x-1=x+3
=>3x-x=3+1
=>2x=4
=>\(x=\dfrac{4}{2}=2\)
f: 15-7x=9-3x
=>-7x+3x=9-15
=>-4x=-6
=>x=1,5
g: x-3=18
=>x=18+3=21
h: 2x+1=15-5x
=>2x+5x=15-1
=>7x=14
=>\(x=\dfrac{14}{7}=2\)
i: 3x-2=2x+5
=>3x-2x=2+5
=>x=7
k: -4x+8=0
=>-4x=-8
=>\(x=\dfrac{-8}{-4}=2\)
l: 2x+3=0
=>2x=-3
=>\(x=-\dfrac{3}{2}\)
m: 4x+5=3x
=>4x-3x=-5
=>x=-5

a: |x-4|=1
=>\(\left[{}\begin{matrix}x-4=1\\x-4=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\left(nhận\right)\\x=3\left(loại\right)\end{matrix}\right.\)
Khi x=5 thì \(B=\dfrac{5+1}{5-3}=\dfrac{6}{2}=3\)
b: \(A=\dfrac{x}{x-3}-\dfrac{x+1}{x+3}+\dfrac{3x-3}{9-x^2}\)
\(=\dfrac{x}{x-3}-\dfrac{x+1}{x+3}-\dfrac{3x-3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x\left(x+3\right)-\left(x+1\right)\left(x-3\right)-3x+3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2+3x-\left(x^2-2x-3\right)-3x+3}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2+3-x^2+2x+3}{\left(x-3\right)\left(x+3\right)}=\dfrac{2x+6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x-3}\)
c: \(M=B:A=\dfrac{2}{x-3}:\dfrac{x}{x-3}=\dfrac{2}{x}\)
Để M=5 thì 2/x=5
=>\(x=\dfrac{2}{5}\left(nhận\right)\)
d: \(N=B-A=\dfrac{2}{x-3}-\dfrac{x}{x-3}=\dfrac{2-x}{x-3}\)
Để N là số nguyên thì \(2-x⋮x-3\)
=>\(x-2⋮x-3\)
=>\(x-3+1⋮x-3\)
=>\(1⋮x-3\)
=>\(x-3\in\left\{1;-1\right\}\)
=>\(x\in\left\{4;2\right\}\)

Bài 19:
Gọi số sản phẩm tổ 1 làm được trong tháng đầu là x(sản phẩm)
(Điều kiện: \(x\in Z^+\))
Số sản phẩm tổ 2 làm được trong tháng đầu là:
800-x(sản phẩm)
Số sản phẩm tổ 1 làm đươc trong tháng hai là:
\(\left(1+15\%\right)\cdot x=1,15x\left(sảnphẩm\right)\)
Số sản phẩm tổ 2 làm được trong tháng hai là:
\(\left(1+20\%\right)\left(800-x\right)=1,2\left(800-x\right)\left(sảnphẩm\right)\)
Tổng số sản phẩm hai tổ làm được trong tháng hai là 945 sản phẩm nên ta có:
1,15x+1,2(800-x)=945
=>1,15x+960-1,2x=945
=>-0,05x=-15
=>x=300(nhận)
Vậy: Trong tháng đầu, tổ 1 làm được 300 sản phẩm, tổ 2 làm được 800-300=500 sản phẩm

a: PA là đường cao ứng với đỉnh P của ΔMNP
=>PA\(\perp\)MN
b: Xét ΔMIN vuông tại I và ΔMAP vuông tại A có
\(\widehat{IMN}\) chung
Do đó: ΔMIN~ΔMAP
c: Xét ΔPIN vuông tại I và ΔPKM vuông tại K có
\(\widehat{IPN}\) chung
Do đó: ΔPIN~ΔPKM
=>\(\dfrac{PI}{PK}=\dfrac{PN}{PM}\)
=>\(\dfrac{PI}{PN}=\dfrac{PK}{PM}\)
Xét ΔPIK và ΔPNM có
\(\dfrac{PI}{PN}=\dfrac{PK}{PM}\)
\(\widehat{IPK}\) chung
Do đó: ΔPIK~ΔPNM
=>\(\widehat{PIK}=\widehat{PNM}\)
d: Xét ΔMIH vuông tại I và ΔMKP vuông tại K có
\(\widehat{IMH}\) chung
Do đó: ΔMIH~ΔMKP
=>\(\dfrac{MI}{MK}=\dfrac{MH}{MP}\)
=>\(MI\cdot MP=MH\cdot MK\)
e: \(\dfrac{PI}{PN}=\dfrac{PK}{PM}\)
=>\(PI\cdot PM=PK\cdot PN\)
\(MH\cdot MK+PK\cdot PN=PI\cdot PM+MI\cdot MP\)
\(=MP\left(PI+MI\right)=MP^2\)

Thay x=-1 và y=2 vào y=(3-2m)x+1, ta được:
-(3-2m)+1=2
=>-3+2m=1
=>2m=4
=>m=2

Khoảng cách giữa xe máy và ô tô sau 6 giờ là
45 x 6 = 270 [km]
Hiệu vận tốc là
60 - 45 = 15 [km/giờ]
Thời đi để ô tô đuổi kịp xe máy là
270 : 15 = 18 [giờ]
Đáp số : 18 giờ

\(\dfrac{x}{5}-\dfrac{x}{2}=9\)
=>\(\dfrac{2x-5x}{10}=9\)
=>\(-\dfrac{3x}{10}=9\)
=>\(3x=-10\cdot9=-90\)
=>\(x=-\dfrac{90}{3}=-30\)

a: Thay m=3 vào phương trình, ta được:
\(\left(3-2\right)x=3\)
=>1*x=3
=>x=3
b: Thay m=2 vào phương trình, ta được:
\(\left(2^2-4\cdot2+9\right)x=x-4\)
=>\(\left(4-8+9\right)x-x=-4\)
=>4x=-4
=>x=-1

bài 7:
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
b: BC=BH+CH=4+9=13(cm)
ΔABC~ΔHBA
=>\(\dfrac{AB}{HB}=\dfrac{BC}{BA}\)
=>\(AB^2=BH\cdot BC=4\cdot13=52\)
=>\(AB=\sqrt{52}=2\sqrt{13}\left(cm\right)\)
Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB~ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC=4\cdot9=36\)
=>\(HA=\sqrt{36}=6\left(cm\right)\)
Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
=>DE=AH=6(cm)
c: Xét ΔADH vuông tại D và ΔAHB vuông tại H có
\(\widehat{DAH}\) chung
Do đó: ΔADH~ΔAHB
=>\(\dfrac{AD}{AH}=\dfrac{AH}{AB}\)
=>\(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAEH vuông tại Evà ΔAHC vuông tại H có
\(\widehat{EAH}\) chung
Do đó: ΔAEH~ΔAHC
=>\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\)
=>\(AH^2=AE\cdot AC\left(2\right)\)
Từ (1),(2) suy ra \(AD\cdot AB=AE\cdot AC\)
ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>\(\widehat{MAC}=\widehat{MCA}\)
\(AD\cdot AB=AE\cdot AC\)
=>\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét ΔADE vuông tại A và ΔACB vuông tại A có
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Do đó: ΔADE~ΔACb
=>\(\widehat{AED}=\widehat{ABC}\)
\(\widehat{AED}+\widehat{MAC}=\widehat{ABC}+\widehat{ACB}=90^0\)
=>DE\(\perp\)AM
Bài 8:
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{DAB}\) chung
Do đó: ΔADB~ΔAEC
=>\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
=>\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
=>\(AD\cdot AC=AB\cdot AE\)
b: Xét ΔADE và ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
\(\widehat{DAE}\) chung
DO đó: ΔADE~ΔABC
c: Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔACB
=>AH\(\perp\)BC tại F
Xét ΔAMF vuông tại M và ΔAFB vuông tại F có
\(\widehat{MAF}\) chung
Do đó: ΔAMF~ΔAFB
=>\(\dfrac{AM}{AF}=\dfrac{AF}{AB}\)
=>\(AF^2=AM\cdot AB\left(3\right)\)
Xét ΔANF vuông tại N và ΔAFC vuông tại F có
\(\widehat{FAN}\) chung
Do đó: ΔANF~ΔAFC
=>\(\dfrac{AN}{AF}=\dfrac{AF}{AC}\)
=>\(AF^2=AN\cdot AC\)(4)
Từ (3),(4) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN và ΔACB có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
\(\widehat{MAN}\) chung
Do đó; ΔAMN~ΔACB
=>\(\widehat{AMN}=\widehat{ACB}\)
=>\(\widehat{AMN}=\widehat{AED}\)
=>ED//MN
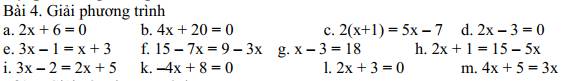
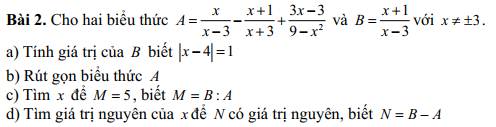



a: 5+2x=20-3x
=>2x+3x=20-5
=>3x=15
=>\(x=\dfrac{15}{3}=5\)
b: \(7-\left(2x+4\right)=-\left(x+4\right)\)
=>\(7-2x-4+x+4=0\)
=>7-x=0
=>x=7
c: \(\left(5x+2\right)-3\left(2x+1\right)=-3x+7\)
=>\(5x+2-6x-3=-3x+7\)
=>-3x+7=-x-1
=>-2x=-8
=>x=4
d: \(2x-\left(3-5x\right)=4\left(x+3\right)\)
=>2x-3+5x=4x+12
=>7x-3=4x+12
=>3x=15
=>\(x=\dfrac{15}{3}=5\)
e: \(5\left(2x-3\right)-4\left(5x-7\right)=19-2\left(x+11\right)\)
=>\(10x-15-20x+28=19-2x-22\)
=>\(-10x+13=-2x-3\)
=>-8x=-16
=>x=2
f: \(x^2-\left(x+2\right)\left(x-2\right)=2x\)
=>\(x^2-\left(x^2-4\right)=2x\)
=>\(2x=x^2-x^2+4=4\)
=>\(x=\dfrac{4}{2}=2\)
g: \(\dfrac{1-3x}{6}+x-1=\dfrac{x+2}{2}\)
=>\(\dfrac{1-3x+6\left(x-1\right)}{6}=\dfrac{3x+6}{6}\)
=>1-3x+6x-6=3x+6
=>3x-5=3x+6
=>-5=6(loại)
h: \(\dfrac{3\left(2x+1\right)}{4}-5-\dfrac{3x+2}{10}=\dfrac{2\left(3x-1\right)}{5}\)
=>\(\dfrac{15\left(2x+1\right)-100-2\left(3x+2\right)}{20}=\dfrac{8\left(3x-1\right)}{20}\)
=>30x+15-100-6x-4=24x-8
=>24x-89=24x-8
=>-89=-8(vô lý)