Bài II (2,0 điểm) Giải toán sau bằng cách lập hệ phương trình:
Hai công nhân cùng làm chung một công việc thì sau 6 giờ làm xong. Nếu người công nhân thứ nhất làm riêng trong 3 giờ rồi dừng lại và người công nhân thứ hai làm tiếp công việc đó trong 1,5 giờ thì cả hai công nhân đã hoàn thành được 40% công việc. Hỏi nếu mỗi công nhân làm riêng thì trong bao nhiêu giờ mới xong công việc trên?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Em tự giải
b.
Ta có \(\widehat{ACB}=\widehat{ADE}\) (cùng phụ \(\widehat{CDE}\))
Mà \(\widehat{ADE}=\widehat{AFE}\) (theo câu a)
\(\Rightarrow\widehat{ACB}=\widehat{AFE}\) (1)
Lại có \(\widehat{AFE}+\widehat{BFE}=180^0\) (kề bù)
\(\Rightarrow\widehat{ACB}+\widehat{BFE}=180^0\)
\(\Rightarrow BCEF\) nội tiếp
\(\widehat{AFE}=\widehat{MFB}\) (đối đỉnh) (2)
Từ (1);(2) \(\Rightarrow\widehat{MFB}=\widehat{ACB}\) hay \(\widehat{MFB}=\widehat{MCE}\)
Xét 2 tam giác MFB và MCE có:
\(\left\{{}\begin{matrix}\widehat{MFB}=\widehat{MCE}\left(cmt\right)\\\widehat{FMB}-chung\end{matrix}\right.\)
\(\Rightarrow\Delta MFB\sim\Delta MCE\left(g.g\right)\)
\(\Rightarrow\dfrac{MB}{ME}=\dfrac{MF}{MC}\Rightarrow MB.MC=MF.ME\)
c.
Bốn điểm A, N, B, C cùng thuộc (O) \(\Rightarrow\widehat{MAC}+\widehat{NBC}=180^0\)
Mà \(\widehat{NBC}+\widehat{MBN}=180^0\) (kề bù)
\(\Rightarrow\widehat{MBN}=\widehat{MAC}\)
Xét hai tam giác MBN và MAC có:
\(\left\{{}\begin{matrix}\widehat{BMN}-chung\\\widehat{MBN}=\widehat{MAC}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta MBN\sim\Delta MAC\left(g.g\right)\)
\(\Rightarrow\dfrac{MB}{MA}=\dfrac{MN}{MC}\Rightarrow MB.MC=MA.MN\)
Kết hợp câu b \(\Rightarrow ME.MF=MA.MN\) \(\Rightarrow\dfrac{ME}{MN}=\dfrac{MA}{MF}\)
Xét 2 tam giác MEA và MNF có:
\(\left\{{}\begin{matrix}\widehat{EMA}-chung\\\dfrac{ME}{MN}=\dfrac{MA}{MF}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta MEA\sim\Delta MNF\left(c.g.c\right)\)
\(\Rightarrow\widehat{MEA}=\widehat{MNF}\)
Mà \(\widehat{MNF}+\widehat{ANF}=180^0\) (kề bù)
\(\Rightarrow\widehat{MEA}+\widehat{ANF}=180^0\)
\(\Rightarrow ANFE\) nội tiếp
Kết hợp câu a \(\Rightarrow A,N,F,D,E\) cùng thuộc 1 đường tròn
Cũng do 5 điểm nói trên cùng thuộc 1 đường tròn \(\Rightarrow\widehat{AND}=\widehat{AFD}=90^0\) (cùng chắn AD)
\(\Rightarrow\widehat{ANI}=90^0\)
\(\Rightarrow AI\) là 1 đường kính của (O) hay A, I, O thẳng hàng
Qua A kẻ tiếp tuyến Ax của (O)
Ta có \(\widehat{BAx}=\widehat{ACB}\) (cùng chắn AB) (3)
Từ (1);(3) \(\Rightarrow\widehat{BAx}=\widehat{AFE}\)
\(\Rightarrow Ax||EF\) (hai góc so le trong bằng nhau)
Mà \(Ax\perp AI\Rightarrow EF\perp AI\)
Hay \(EF\perp OI\) (do A, O, I thẳng hàng)


a: \(\text{Δ}=\left(-2m\right)^2-4\left(m^2-m+1\right)\)
\(=4m^2-4m^2+4m-4=4m-4\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>4m-4>0
=>4m>4
=>m>1
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m\\x_1x_2=\dfrac{c}{a}=m^2-m+1\end{matrix}\right.\)
\(A=x_1x_2-x_1-x_2\)
\(=m^2-m+1-\left(x_1+x_2\right)\)
\(=m^2-3m+1=m^2-3m+\dfrac{9}{4}-\dfrac{5}{4}\)
\(=\left(m-\dfrac{3}{2}\right)^2-\dfrac{5}{4}>=-\dfrac{5}{4}\forall m\)
Dấu '=' xảy ra khi \(m-\dfrac{3}{2}=0\)
=>\(m=\dfrac{3}{2}\)

Ta có:
\(a^4+\dfrac{1}{4}=\left(a^2+\dfrac{1}{2}\right)^2-a^2=\left(a^2+a+\dfrac{1}{2}\right)\left(a^2-a+\dfrac{1}{2}\right)\)
\(=\left(a^2+a+\dfrac{1}{2}\right)\left(a^2-2a+1+a-1+\dfrac{1}{2}\right)\)
\(=\left(a^2+a+\dfrac{1}{2}\right)\left[\left(a-1\right)^2+\left(a-1\right)+\dfrac{1}{2}\right]\)
Do đó:
\(K=\dfrac{\left(2^2+2+\dfrac{1}{2}\right)\left(1^2+1+\dfrac{1}{2}\right)...\left(\left(2n\right)^2+2n+\dfrac{1}{2}\right)\left(\left(2n-1\right)^2+\left(2n-1\right)+\dfrac{1}{2}\right)}{\left(1^2+1+\dfrac{1}{2}\right)\left(0^2+0+\dfrac{1}{2}\right)...\left(\left(2n-1\right)^2+\left(2n-1\right)+\dfrac{1}{2}\right)\left(\left(2n-2\right)^2+\left(2n-2\right)+\dfrac{1}{2}\right)}\)
\(=\dfrac{\left(2n\right)^2+2n+\dfrac{1}{2}}{0^2+0+\dfrac{1}{2}}=8n^2+4n+1\)
\(=\left(2n\right)^2+\left(2n+1\right)^2\) là tổng của 2 SCP
ai giải hộ em câu này với
cho 30g hôn hợp c2h5oh với ch3cooh phản ứng hết với 100ml NaOH 1M
a) tính phần trăm kl các chất ban đầu
b)tính kl Na cần để phản ứng với lượng c2h5oh

ΔHAB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(AB=\sqrt{2^2+1^2}=\sqrt{5}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(HC=\dfrac{2^2}{1}=4\left(cm\right)\)
BC=BH+CH
=4+1=5(cm)
ΔHAC vuông tại H
=>\(HA^2+HC^2=AC^2\)
=>\(AC=\sqrt{2^2+4^2}=2\sqrt{5}\left(cm\right)\)
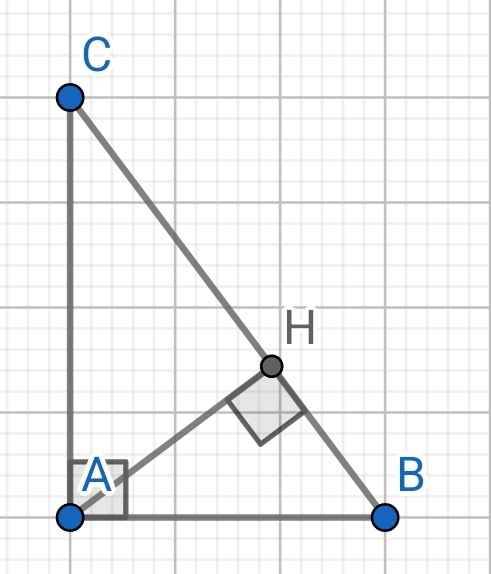
∆ABC vuông tại A, AH là đường cao
⇒ AH² = BH.CH
⇒ CH = AH² : BH
= 2² : 1
= 4 (cm)
⇒ BC = BH + CH
= 1 + 4 = 5 (cm)
∆ABH vuông tại H
⇒ AB² = AH² + BH² (Pytago)
= 2² + 1²
= 5
AB = √5 (cm)
∆AHC vuông tại H
⇒ AC² = AH² + CH² (Pytago)
= 2² + 4²
= 20
⇒ AC = 2√5 (cm)

Có \(2020\left(\dfrac{a^2}{b}+\dfrac{b^2}{c}+\dfrac{c^2}{a}\right)+\dfrac{1}{3}\left(a^2+b^2+c^2\right)\)
\(\ge2020.\dfrac{\left(a+b+c\right)^2}{b+c+a}+\dfrac{\left(a+b+c\right)^2}{9}\)
(áp dụng BĐT \(\dfrac{x^2}{a}+\dfrac{y^2}{b}+\dfrac{z^2}{c}\ge\dfrac{\left(x+y+z\right)^2}{a+b+c}\) và \(3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\))
\(=2020\left(a+b+c\right)+\dfrac{\left(a+b+c\right)^2}{9}\)
\(=2020+\dfrac{1}{9}\) (vì \(a+b+c=1\))
\(=\dfrac{18181}{9}\)
Vậy GTNN là \(\dfrac{18181}{9}\) khi \(a=b=c=\dfrac{1}{3}\)

Áp dụng Bunhiacopxki:
\(\left(a+1\right)^2=\left(\sqrt{ab}.\sqrt{\dfrac{a}{b}}+1.1\right)^2\le\left(ab+1\right)\left(\dfrac{a}{b}+1\right)=\dfrac{\left(ab+1\right)\left(a+b\right)}{b}\)
\(\Rightarrow\dfrac{1}{\left(a+1\right)^2}\ge\dfrac{b}{\left(ab+1\right)\left(a+b\right)}\)
Tương tự: \(\dfrac{1}{\left(b+1\right)^2}\ge\dfrac{a}{\left(ab+1\right)\left(a+b\right)}\)
\(\Rightarrow\dfrac{1}{\left(a+1\right)^2}+\dfrac{1}{\left(b+1\right)^2}\ge\dfrac{b}{\left(ab+1\right)\left(a+b\right)}+\dfrac{a}{\left(ab+1\right)\left(a+b\right)}=\dfrac{1}{ab+1}\)
Mà \(abc=1\Rightarrow ab=\dfrac{1}{c}\)
\(\Rightarrow\dfrac{1}{\left(a+1\right)^2}+\dfrac{1}{\left(b+1\right)^2}\ge\dfrac{1}{\dfrac{1}{c}+1}=\dfrac{c}{c+1}\)
Theo nguyên lý Dirichlet, trong 3 số a;b;c luôn có ít nhất 2 số cùng phía so với 1. Không mất tính tổng quát, giả sử đó là a và b
\(\Rightarrow\left(a-1\right)\left(b-1\right)\ge0\)
\(\Rightarrow ab+1\ge a+b\)
\(\Rightarrow2ab+2\ge ab+a+b+1=\left(a+1\right)\left(b+1\right)\)
\(\Rightarrow\dfrac{2}{\left(a+1\right)\left(b+1\right)}\ge\dfrac{1}{ab+1}\)
\(\Rightarrow\dfrac{2}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}\ge\dfrac{1}{\left(ab+1\right)\left(c+1\right)}=\dfrac{1}{\left(\dfrac{1}{c}+1\right)\left(c+1\right)}=\dfrac{c}{\left(c+1\right)^2}\)
Gọi vế trái BĐT cần c/m là P
\(\Rightarrow P\ge\dfrac{c}{c+1}+\dfrac{1}{\left(c+1\right)^2}+\dfrac{c}{\left(c+1\right)^2}=1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)

\(\text{Δ}=\left[-\left(m+1\right)\right]^2-4\cdot1\cdot\left(-3\right)=\left(m+1\right)^2+12>=12>0\forall x\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m+1\\x_1x_2=\dfrac{c}{a}=-3\end{matrix}\right.\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1-x_2=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x_1=m+1+4=m+5\\x_1-x_2=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_1=0,5m+2,5\\x_2=x_1-4=0,5m+2,5-4=0,5m-1,5\end{matrix}\right.\)
\(x_1x_2=-3\)
=>\(\left(0,5m+2,5\right)\left(0,5m-1,5\right)=-3\)
=>\(0,25m^2-0,75m+1,25m-3,75+3=0\)
=>\(0,25m^2+0,5m-0,75=0\)
=>\(\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\)
\(ac=-3< 0\Rightarrow\) pt luôn có 2 nghiệm trái dấu với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1x_2=-3\end{matrix}\right.\)
Kết hợp với điều kiện đề bài ta được:
\(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1-x_2=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{m+5}{2}\\x_2=\dfrac{m-3}{2}\end{matrix}\right.\)
Thay vào \(x_1x_2=-3\)
\(\left(\dfrac{m+5}{2}\right)\left(\dfrac{m-3}{2}\right)=-3\)
\(\Rightarrow...\) (em tự giải pt bậc 2 ra m)


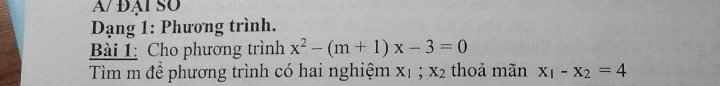
Gọi thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là x(giờ) và y(giờ)
(ĐK: x>0; y>0)
Trong 1 giờ, người thứ nhất làm được: \(\dfrac{1}{x}\left(côngviệc\right)\)
Trong 1 giờ, người thứ hai làm được: \(\dfrac{1}{y}\left(côngviệc\right)\)
Trong 1 giờ, hai người làm được: \(\dfrac{1}{6}\left(côngviệc\right)\)
Do đó, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\left(1\right)\)
Trong 3 giờ, người thứ nhất làm được \(\dfrac{3}{x}\)(công việc)
Trong 1,5 giờ, người thứ hai làm được \(\dfrac{1.5}{y}\left(côngviệc\right)\)
Nếu người thứ nhất làm trong 3 giờ và người thứ hai làm trong 1,5 giờ thì hai người làm được 40% công việc nên ta có:
\(\dfrac{3}{x}+\dfrac{1.5}{y}=\dfrac{2}{5}\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{3}{x}+\dfrac{1.5}{y}=\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{1}{2}\\\dfrac{3}{x}+\dfrac{1.5}{y}=\dfrac{2}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1.5}{y}=\dfrac{1}{2}-\dfrac{2}{5}=\dfrac{1}{10}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=15\\\dfrac{1}{x}=\dfrac{1}{6}-\dfrac{1}{15}=\dfrac{3}{30}=\dfrac{1}{10}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=10\\y=15\end{matrix}\right.\left(nhận\right)\)
Vậy: thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là 10(giờ) và 15(giờ)