hiện tại, và những ngày trước, mình bị các bạn quấy rối bao cáo câu hỏi, tại sao nhỉ? các câu hỏi của mình có gì sai đâu, mình bị nhắc nhở thôi. có nhiều độ tuổi còn nhỏ hơn mình nữa mà sinh thói phá phách rồi. mà mình chỉ nhắc nhở các bạn thôi mà, nhiều lúc mình thấy phiền đó nhưng mình chưa bao giờ báo cáo ai hết. không ngờ mình chỉ hù dọa cho các bạn sợ thôi, chứ không có ý gì hết. mình thấy các bạn quá đáng lắm rồi đó. năm nay mình lớp 8 rồi, mà khi mình bị quản trị viên nhắc nhở là mình tức giận, nhưng mình nhịn các bạn đấy. đừng quá đáng, mình tính tình nhẹ nhàng nhưng mà ai chọc mình. chơi ném đá giấu tay là mình không nhịn nữa đâu.bộ coi mình hiền là báo cáo? mình bị trừ điểm rồi đấy. và mình đăng bài này khuyên các bạn thôi chứ không học thì thôi để người ta học với thứ 3 tuần sau mình thi rồi đâu phải ngồi thảnh thơi đi nhắc nhở các bạn đâu? làm ơn cho mình học với nhé thứ 3 là mình thi rồi!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
=>\(BA^2=BH\cdot BC\)
b: Xét ΔCED vuông tại E và ΔCHA vuông tại H có
\(\widehat{ECD}\) chung
Do đó: ΔCED~ΔCHA
=>\(\dfrac{CE}{CH}=\dfrac{CD}{CA}\)
=>\(\dfrac{CE}{CD}=\dfrac{CH}{CA}\)
=>\(CE\cdot CA=CD\cdot CH\)
Xét ΔCEH và ΔCDA có
\(\dfrac{CE}{CD}=\dfrac{CH}{CA}\)
\(\widehat{ECH}\) chung
Do đó: ΔCEH~ΔCDA
=>\(\widehat{CHE}=\widehat{CAD}\)
mà \(\widehat{CAD}+\widehat{BAD}=\widehat{BAC}=90^0\)
và \(\widehat{CHE}+\widehat{AHE}=\widehat{CHA}=90^0\)
nên \(\widehat{BAD}=\widehat{AHE}\)
Xét ΔBAD và ΔAHE có
\(\widehat{BAD}=\widehat{AHE}\)
\(\widehat{ABD}=\widehat{HAE}\)
Do đó: ΔBAD~ΔAHE
c: ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}=90^0\)
\(\widehat{BDA}+\widehat{HAD}=90^0\)(ΔHAD vuông tại H)
mà \(\widehat{BAD}=\widehat{BDA}\)(ΔBAD cân tại B)
nên \(\widehat{CAD}=\widehat{HAD}\)
=>AD là phân giác của góc HAC
Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
\(\widehat{HAD}=\widehat{EAD}\)
Do đó: ΔAHD=ΔAED
=>AH=AE
=>ΔAHE cân tại A
=>AD\(\perp\)HE
mà HE//AF
nên AD\(\perp\)AF
=>AF là phân giác góc ngoài tại A của ΔAHC
Xét ΔAHC có AF là phân giác ngoài
nên \(\dfrac{FH}{FC}=\dfrac{AH}{AC}\left(1\right)\)
Xét ΔAHC có AD là phân giác
nên \(\dfrac{AH}{AC}=\dfrac{DH}{DC}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{FH}{FC}=\dfrac{DH}{DC}\)
=>\(FH\cdot DC=DH\cdot FC\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
=>\(BA^2=BH\cdot BC\)
b: Xét ΔCED vuông tại E và ΔCHA vuông tại H có
\(\widehat{ECD}\) chung
Do đó: ΔCED~ΔCHA
=>\(\dfrac{CE}{CH}=\dfrac{CD}{CA}\)
=>\(\dfrac{CE}{CD}=\dfrac{CH}{CA}\)
=>\(CE\cdot CA=CD\cdot CH\)
Xét ΔCEH và ΔCDA có
\(\dfrac{CE}{CD}=\dfrac{CH}{CA}\)
\(\widehat{ECH}\) chung
Do đó: ΔCEH~ΔCDA
=>\(\widehat{CHE}=\widehat{CAD}\)
mà \(\widehat{CAD}+\widehat{BAD}=\widehat{BAC}=90^0\)
và \(\widehat{CHE}+\widehat{AHE}=\widehat{CHA}=90^0\)
nên \(\widehat{BAD}=\widehat{AHE}\)
Xét ΔBAD và ΔAHE có
\(\widehat{BAD}=\widehat{AHE}\)
\(\widehat{ABD}=\widehat{HAE}\)
Do đó: ΔBAD~ΔAHE
c: ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}=90^0\)
\(\widehat{BDA}+\widehat{HAD}=90^0\)(ΔHAD vuông tại H)
mà \(\widehat{BAD}=\widehat{BDA}\)(ΔBAD cân tại B)
nên \(\widehat{CAD}=\widehat{HAD}\)
=>AD là phân giác của góc HAC
Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
\(\widehat{HAD}=\widehat{EAD}\)
Do đó: ΔAHD=ΔAED
=>AH=AE
=>ΔAHE cân tại A
=>AD\(\perp\)HE
mà HE//AF
nên AD\(\perp\)AF
=>AF là phân giác góc ngoài tại A của ΔAHC
Xét ΔAHC có AF là phân giác ngoài
nên \(\dfrac{FH}{FC}=\dfrac{AH}{AC}\left(1\right)\)
Xét ΔAHC có AD là phân giác
nên \(\dfrac{AH}{AC}=\dfrac{DH}{DC}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{FH}{FC}=\dfrac{DH}{DC}\)
=>\(FH\cdot DC=DH\cdot FC\)

b: Để đường thẳng y=(m+1)x+2 song song với đường thẳng y=-2x+1 thì \(\left\{{}\begin{matrix}m+1=-2\\2\ne1\left(đúng\right)\end{matrix}\right.\)
=>m+1=-2
=>m=-3
a: 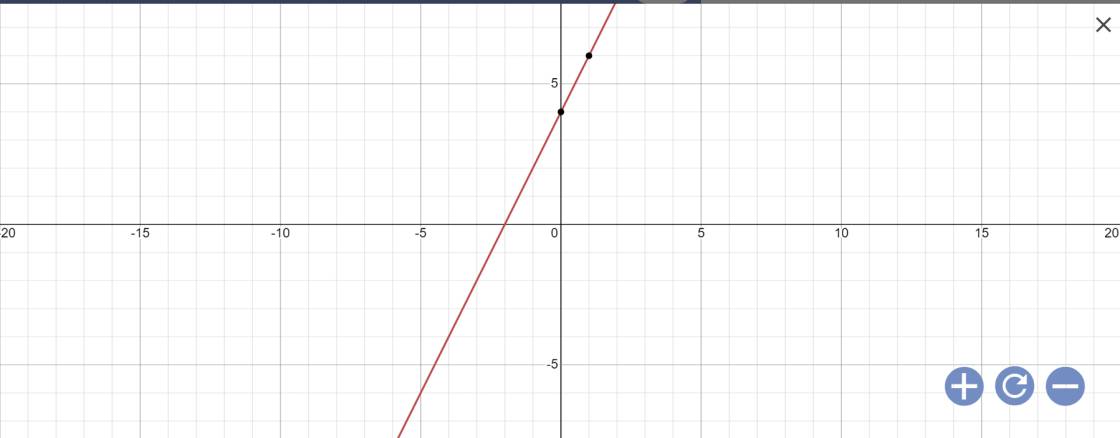

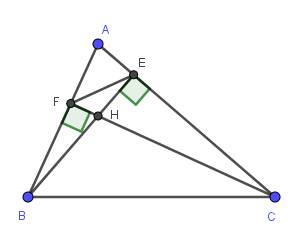
a) Xét hai tam giác vuông: \(\Delta BHF\) và \(\Delta CHE\) có:
\(\widehat{BHF}=\widehat{CHE}\) (đối đỉnh)
\(\Rightarrow\Delta BHF\) ∽ \(\Delta CHE\) (g-g)
\(\Rightarrow\dfrac{HB}{HC}=\dfrac{HF}{HE}\)
\(\Rightarrow HE.HB=HC.HF\)
b) Xét hai tam giác vuông: \(\Delta AFC\) và \(\Delta AEB\) có:
\(\widehat{A}\) chung
\(\Rightarrow\Delta AFC\) ∽ \(\Delta AEB\) (g-g)
\(\Rightarrow\dfrac{AF}{AE}=\dfrac{AC}{AB}\)
\(\Rightarrow\dfrac{AF}{AC}=\dfrac{AE}{AB}\)
Xét \(\Delta AEF\) và \(\Delta ABC\) có:
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\) (cmt)
\(\widehat{A}\) chung
\(\Rightarrow\Delta AEF\) ∽ \(\Delta ABC\) (c-g-c)

MD là phân giác của góc NMP
=>\(\widehat{NMD}=\widehat{PMD}=\dfrac{\widehat{NMP}}{2}=45^0\)
Xét tứ giác EMDN có \(\widehat{EDN}=\widehat{EMN}=90^0\)
nên EMDN là tứ giác nội tiếp
=>\(\widehat{END}+\widehat{EMD}=180^0\)
=>\(\widehat{END}=\widehat{DMP}=45^0\)
Xét ΔDNE vuông tại D có \(\widehat{DNE}=45^0\)
nên ΔDNE vuông cân tại D

Lời giải:
Gọi chiều dài và chiều rộng hcn lớn lần lượt là $a$ cm và $b$ cm
Ta có: $a+b=100:2=50$
Khi chia hcn thành 1 hv và 1 hcn thì ta có 1 hình vuông cạnh $b$ cm và 1 hcn có độ dài 2 chiều là $b$ cm và $a-b$ cm
Chu vi hcn mới: $2(b+a-b)=60$
$\Leftrightarrow a=30$ (cm)
$b=50-a=50-30=20$ (cm)
Vậy độ dài cạnh hcn ban đầu là $20$ cm và $30$ cm

Bài 7:
a: Thay x=1 vào B, ta được:
\(B=\dfrac{2-1}{1}=\dfrac{1}{1}=1\)
b: \(A=\dfrac{1}{x-2}+\dfrac{2x}{x^2-4}+\dfrac{1}{x+2}\)
\(=\dfrac{1}{x-2}+\dfrac{2x}{\left(x-2\right)\left(x+2\right)}+\dfrac{1}{x+2}\)
\(=\dfrac{x+2+2x+x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{4x}{\left(x-2\right)\left(x+2\right)}\)
c: \(A\cdot B=1\)
=>\(\dfrac{4x}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{2-x}{x}=1\)
=>\(\dfrac{-4}{x+2}=1\)
=>x+2=-4
=>x=-6(nhận)

Bài 2:
Gọi vận tốc xe 1 là x(km/h)
(Điều kiện: x>0)
vận tốc xe 2 là x+10(km/h)
Tổng vận tốc hai xe là 200:2=100(km/h)
=>x+x+10=100
=>2x=90
=>x=45(nhận)
vậy: vận tốc của xe 1 là 45km/h
vận tốc của xe 2 là 45+10=55km/h

Olm chào em, vấn đề em hỏi Olm xin hỗ trợ như sau:
Đoạn \(\dfrac{OA}{OC}\) = \(\dfrac{OB}{OD}\) (hệ quả của định lí Thales). Em hiểu rồi đúng chưa.
Từ dòng suy ra \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{OA+OC}{OB+OD}\) = \(\dfrac{AC}{BD}\) là em không hiểu tại sao phải không?
Vậy Olm sẽ giảng cho em như sau:
\(\dfrac{OA}{OC}\) = \(\dfrac{OB}{OD}\) (hệ quả định lí Thales) ⇒ \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) (tc tỉ lệ thức)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{OA+OC}{OB+OD}\) (1)
Mặt khác O là giao điểm của AC và BD nên
\(\left\{{}\begin{matrix}OA+OC=AC\\OB+OD=BD\end{matrix}\right.\) (2)
Thay (2) vào (1) ta có: \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{AC}{BD}\)
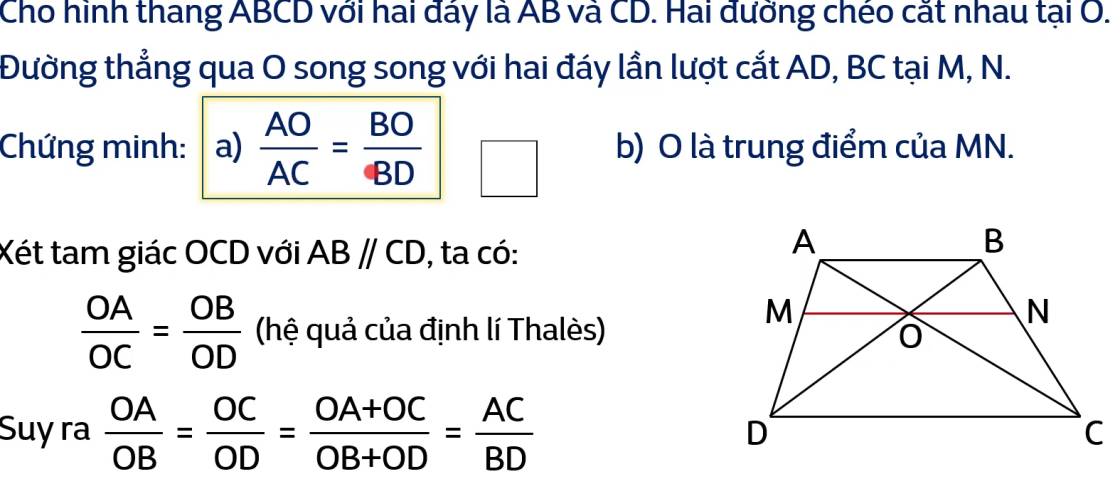
Giải thích đoạn: \(\dfrac{AO}{AC}\) = \(\dfrac{BO}{BD}\)
\(\dfrac{OA}{OB}\) = \(\dfrac{AC}{BD}\) (cmt) ⇒\(\dfrac{AO}{BO}=\dfrac{AC}{BD}\) ⇒ \(\dfrac{AO}{AC}\) = \(\dfrac{BO}{BD}\) (tính chất tỉ lệ thức)
Mọi chi tiết bài giảng liên hệ zalo 0385 168 017
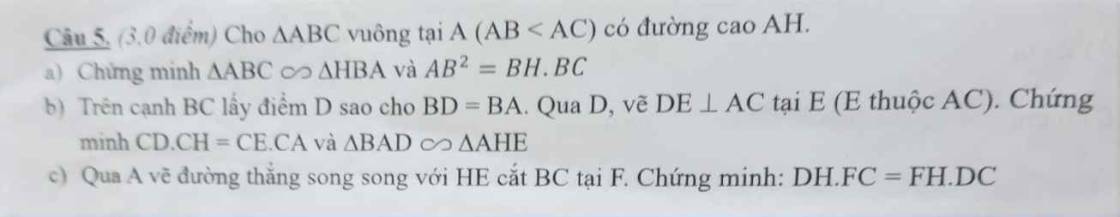



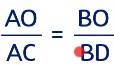
ssssssssssssssssssssssssssss