Sau ngày 1 thì số gạo còn lại chiếm:

\(1-\dfrac{1}{7}=\dfrac{6}{7}\)(tổng số gạo)

Sau ngày 2 thì số gạo còn lại chiếm:

\(\dfrac{6}{7}\left(1-\dfrac{2}{5}\right)=\dfrac{6}{7}\cdot\dfrac{3}{5}=\dfrac{18}{35}\)(tổng số gạo)

Số gạo còn lại sau ngày thứ hai là:

\(150\cdot\dfrac{18}{35}=\dfrac{540}{7}\left(tạ\right)\)

Ngày thứ nhất bán được số gạo là:

     \(150\times\dfrac{1}{7}=\dfrac{150}{7}\) ( tạ )

Ngày thứ hai bán được số gạo là:

     \(\left(150-\dfrac{150}{7}\right)\times\dfrac{2}{5}=\dfrac{360}{7}\) ( tạ )

Trong kho còn lại số tạ gạo là :

     \(150-\dfrac{150}{7}-\dfrac{360}{7}=\dfrac{540}{7}\) ( tạ )

Vậy trong kho còn lại \(\dfrac{540}{7}\) tạ gạo.

Gọi ba số tự nhiên liên tiếp là a;a+1;a+2

Tích hai số sau lớn hơn tích hai số đầu là 192 nên ta có:

\(\left(a+2\right)\left(a+1\right)-a\left(a+1\right)=192\)

=>\(a^2+3a+2-a^2-a=192\)

=>2a+2=192

=>a+1=96

=>a=95

=>a+1=96; a+2=97

vậy: ba số cần tìm là 95;96;97

Gọi 3 STN liên tiếp lần lượt là: \(x;x+1;x+2\left(ĐK:x\inℕ\right)\) 

Tích hai số sau: \(\left(x+1\right)\left(x+2\right)\) và tích hai số đầu: \(x\left(x+1\right)\)

Theo bài ra, ta có:

\(\left(x+1\right)\left(x+2\right)-x\left(x+1\right)=192\\ \Rightarrow x^2+x+2x+2-x^2-x=192\\ \Rightarrow2x=190\\ \Rightarrow x=95\left(TM\right)\)

Vậy 3 STN phải tìm: 95;96;97

\(\dfrac{x}{y}=\dfrac{m}{n}\\ \Rightarrow\dfrac{y}{x}=\dfrac{n}{m},\dfrac{x}{m}=\dfrac{y}{n},\dfrac{m}{x}=\dfrac{n}{y}\)

 Đặt \(P\left(x\right)=x^3+3x^2-x+3^n\)

 Nếu \(P\left(x\right)\) có nghiệm hữu tỉ \(x=\dfrac{p}{q}\left(p\inℤ,q\inℕ^∗;\left(p,q\right)=1\right)\) thì \(p|3^n,q|1\Rightarrow q=1\) và \(p=3^k\left(k\le n\right)\)

 Vậy \(x=3^k\) sẽ là nghiệm hữu tỉ duy nhất của \(P\left(x\right)\) hay \(P\left(3^k\right)=0\)

 \(\Leftrightarrow\left(3^k\right)^3+3.\left(3^k\right)^2-3^k+3^n=0\)

 \(\Leftrightarrow3^{3k}+3^{2k+1}-3^k+3^n=0\)

 \(\Leftrightarrow3^{2k}+3^{k+1}-1+3^{n-k}=0\)

 Ta thấy với \(n>k\) thì \(3^{2k}+3^{k+1}+3^{n-k}⋮3\) và \(0⋮3\) nên từ đây suy ra \(1⋮3\), vô lý.

 Với \(n=k\) thì \(3^{2n}+3^{n+1}=0\), vô lý vì \(3^{2n}+3^{n+1}>0\) với \(n\inℕ^∗\)

 Vậy \(P\left(x\right)\) không thể có nghiệm hữu tỉ. Do đó, nếu \(x^3+3x^2-x+3=0\) thì \(x\) chỉ có thể là một số vô tỉ. (đpcm)

a: \(\dfrac{1}{4003}>0;0>-\dfrac{75}{106}\)

Do đó: \(\dfrac{1}{4003}>-\dfrac{75}{106}\)

b: \(-19< -17\)

=>\(-\dfrac{19}{31}< -\dfrac{17}{31}\)

c: \(\dfrac{-33}{37}>\dfrac{-34}{37}\)

mà \(-\dfrac{34}{37}>-\dfrac{34}{35}\)

nên \(\dfrac{-33}{37}>-\dfrac{34}{35}\)

d: \(\dfrac{-13}{77}=\dfrac{-13\cdot205}{77\cdot205}=\dfrac{-2665}{77\cdot205}\)

\(\dfrac{-34}{205}=\dfrac{-34\cdot77}{205\cdot77}=\dfrac{-2618}{205\cdot77}\)

mà -2665<-2618

nên \(\dfrac{-13}{77}< \dfrac{-34}{205}\)

e: \(\dfrac{-456}{461}=-1+\dfrac{5}{461};\dfrac{-123}{128}=-1+\dfrac{5}{128}\)

461>128

=>\(\dfrac{5}{461}< \dfrac{5}{128}\)

=>\(\dfrac{5}{461}-1< \dfrac{5}{128}-1\)

=>\(\dfrac{-456}{461}< \dfrac{-123}{128}\)

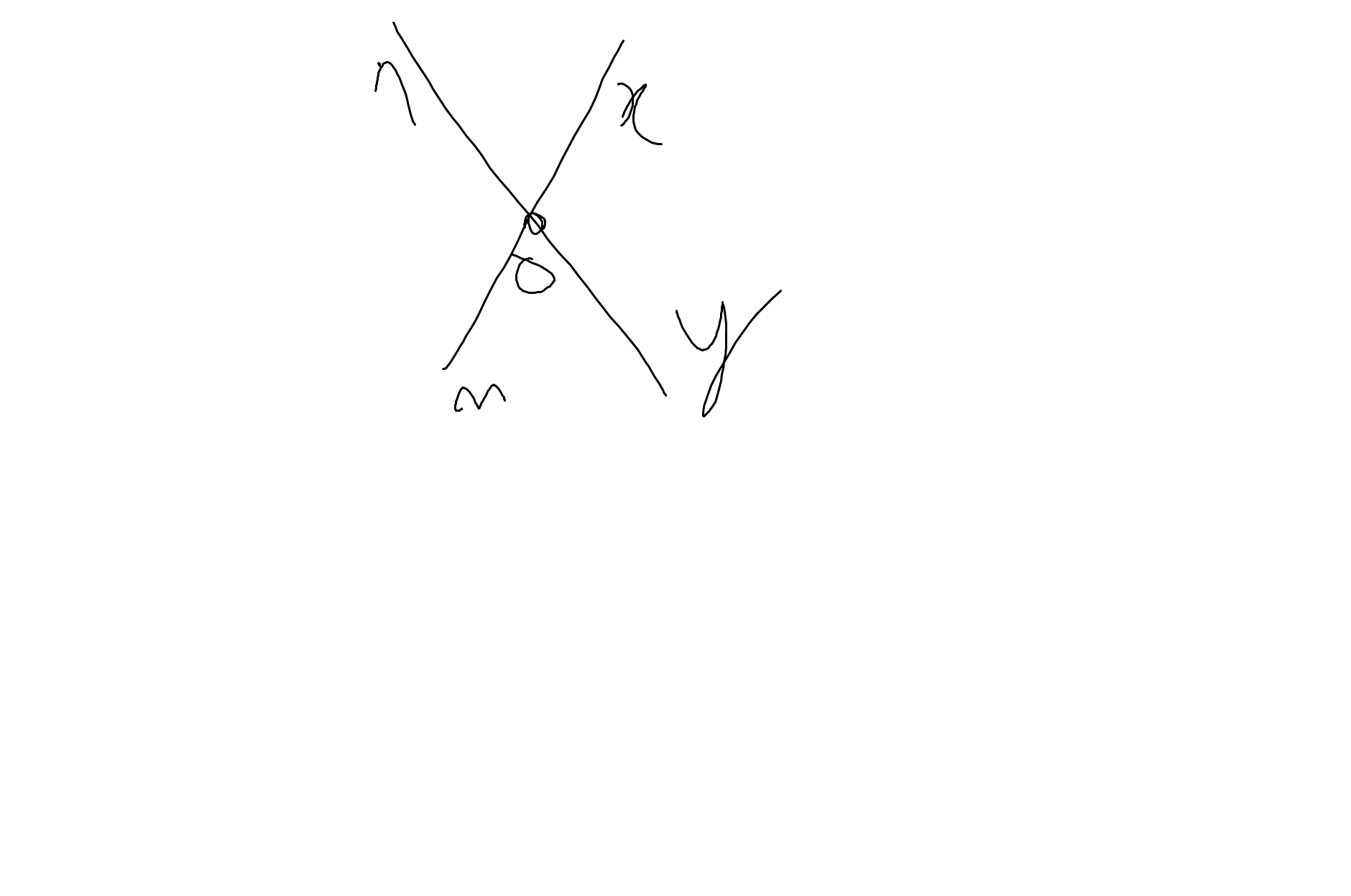
\(\widehat{mOn}=\widehat{xOy}\)(hai góc đối đỉnh)

mà \(\widehat{xOy}=85^0\)

nên \(\widehat{mOn}=85^0\)

Ta có: \(\widehat{nOm}+\widehat{xOn}=180^0\)(hai góc kề bù)

=>\(\widehat{xOn}+85^0=180^0\)

=>\(\widehat{xOn}=180^0-85^0=95^0\)

Ta có: \(\widehat{xOn}=\widehat{yOm}\)(hai góc đối đỉnh)

mà \(\widehat{xOn}=95^0\)

nên \(\widehat{yOm}=95^0\)

\(1,4\left(51\right)=\dfrac{479}{330};3,1\left(45\right)=\dfrac{173}{55}\)

Tổng các tử số là 479+173=652

=>Chọn C

??

2 bạn nhé.