Bài học cùng chủ đề
- Phương pháp quy nạp toán học
- Một số ứng dụng của quy nạp toán học
- Phương pháp quy nạp toán học
- Công thức nhị thức Newton và tam giác Pascal
- Ứng dụng tam giác Pascal trong khai triển nhị thức Newton
- Hệ số trong khai triển nhị thức Newton
- Hệ số trong khai triển nhị thức Newton
- Giải phương trình, hệ phương trình, bất phương trình chứa nhị thức Newton
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Ứng dụng tam giác Pascal trong khai triển nhị thức Newton SVIP

Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
1. Công thức khai triển nhị thức Newton:
Trong khai triển $(a + b)^n$ với $n = 1, 2, 3, 4, 5$ có:
+ $n + 1$ số hạng, trong đó số hạng đầu tiên là $a^n$ và số hạng cuối cùng là $b^n$.
+ tổng số mũ của $a$ và $b$ trong mỗi số hạng đều bằng $n$.
+ số mũ của $a$ giảm 1 đơn vị và số mũ của $b$ tăng 1 đơn vị khi chuyển từ số hạng này đến số hạng tiếp theo (từ trái sang phải).
2. Tam giác Pascal
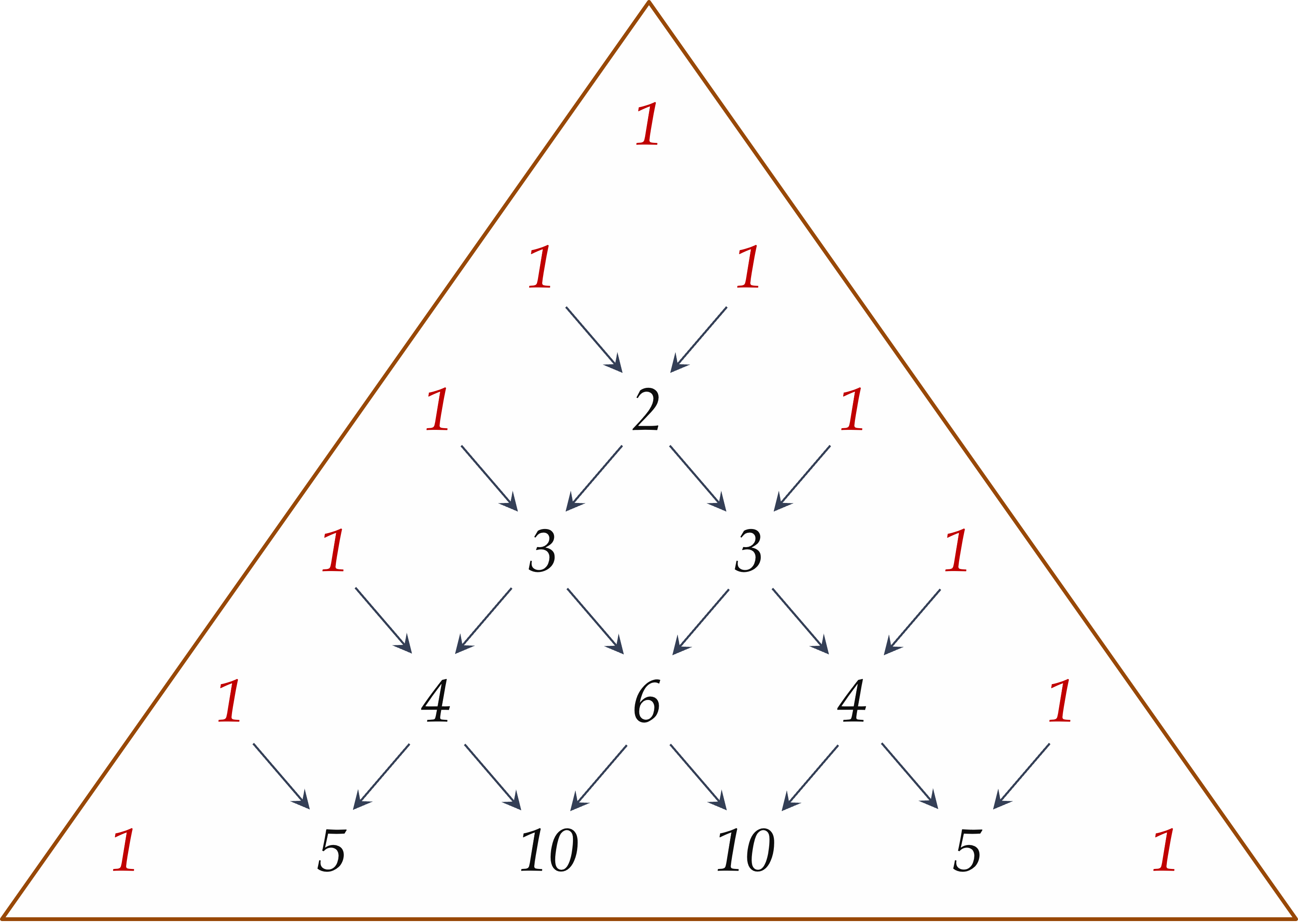
Mọi số khác 1 đều là tổng của hai số ở ngay phía trên nó.
Hoàn thiện hai hàng H5, H6 của tam giác Pascal sau:
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||
| 1 | 6 |
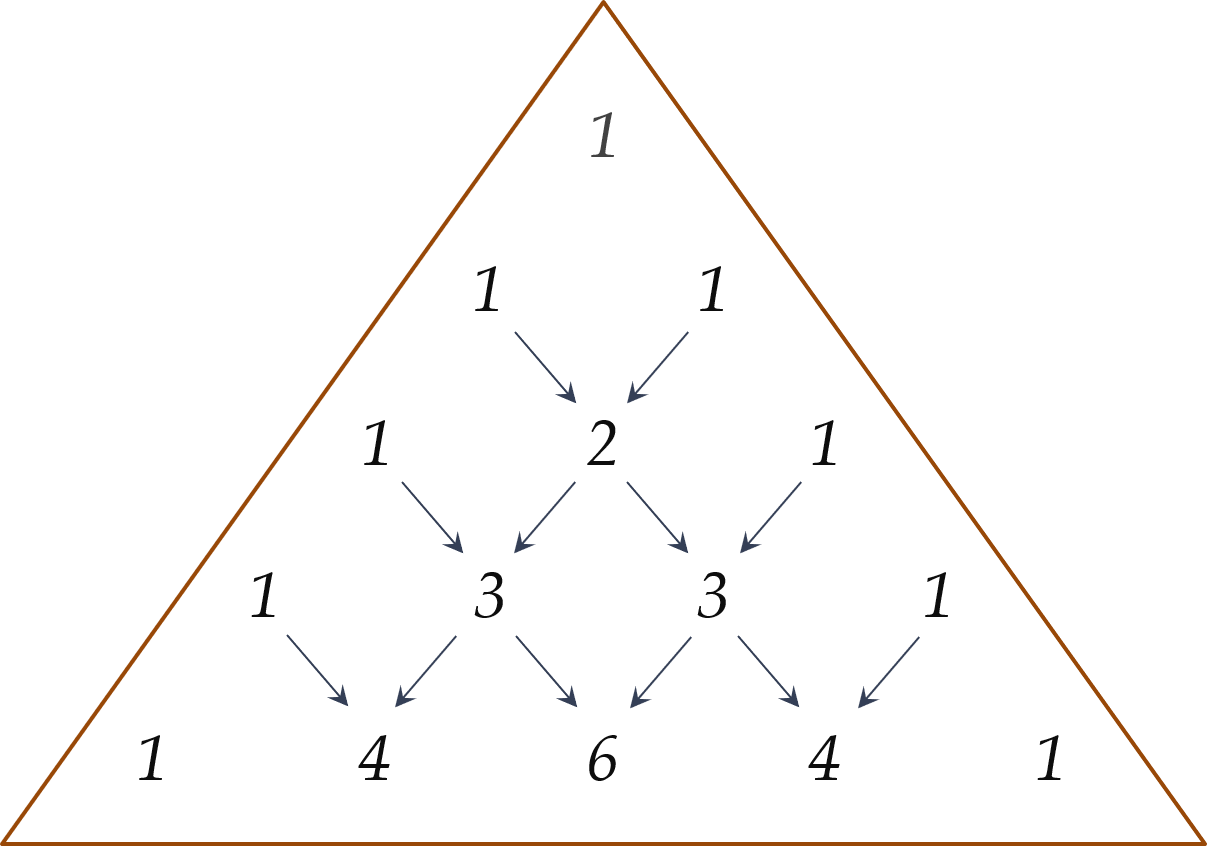
Cho 5 hàng đầu tiên của tam giác Pascal như hình vẽ. Từ đó lựa chọn khai triển của (a+b)5.
Trong khai triển (a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5, thay a=3 và b=−2x ta được (3−2x)5=
Tính: 5.34.(−2x).
So sánh:
C31
- =
- <
- >
- <
- >
- =
Hoàn thành các phép so sánh:
C51= ; C53= .
(Kéo thả hoặc click vào để điền)
Khai triển (1+1)2n+1 có tất cả bao nhiêu số hạng?
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- [âm nhạc]
- dựa vào tam giác pascar này chúng ta có
- thể xác định được hệ số của a + b^6 đó
- là nội dung của phần tiếp theo ứng dụng
- tam giác Pascal trong khai triển nhị
- thức Newton
- ở trong tam giác pascar này thầy sẽ gọi
- hàng thứ nhất tức là ứng với a + b mũ 0
- ấy N = 0 là hàng không tiếp theo là hàng
- 1 hàng 2 hàng 3 hàng 4 và hàng năm Vậy
- thì để xác định a + b^6 ở trong hỏi chấm
- 1 thì ta cần xác định hàm H6 để xác định
- H6 thầy sẽ xuất phát từ H5
- hàng 6 thì hai bên chắc chắn là một và
- một rồi ứng với hệ số của a mũ 6 và b mũ
- 6 còn hệ số của a mũ 5 b mũ 1 đấy sẽ
- bằng tổng của hai số hạng ở ngay phía
- trên tức là bằng 1 + 5 tương tự như vậy
- ta xác định được các số hạng Còn lại
- 1 + 5 thì bằng 6 ta sẽ viết này a mũ 6
- tiếp theo là 6 a mũ 5 b mũ 1 tương tự
- như vậy 5 + 10 thì bằng 15
- 10 + 10 = 20 10 + 5 = 15 và 6 nên ta sẽ
- có hệ số của 4 số hạng tiếp theo là
- 15a^4 b mũ 2 cộng 20a^3 b^3 + 15A bình b
- mũ 4 + 6A b^5 và cuối cùng là cộng với b
- mũ 6 như vậy ta có khai triển của a + b
- mũ 6 như thế này
- và Đó cũng là cách các bạn sử dụng làm
- ra Pascal để viết để tìm hệ số trong 1
- khai triển với a + b mũ n với n lớn hơn
- 5 tương tự như vậy hối hận sẽ trả lời
- cho thầy câu hỏi họ chấm hai là viết
- khai triển 3 - 2x^5 bằng cách sử dụng
- tam giác Pascal
- Nếu như các bạn không thể ghi nhớ được
- công thức khai triển của a + b tất cả mũ
- 5 ý thì các bạn có thể xuất phát từ hẳn
- là thức a + b bình minh tức là a + b mũ
- n trong trường hợp N bằng 2 rồi sử dụng
- tam giác Pascal suy giảm ra hàng số 3
- hàng số 4 rồi đến hàng số 5
- chính xác và như vậy ta sẽ viết khai
- triển a + b^5 sau đó thay A là 3 còn b
- là là -2x nhất không phải là 2x đâu
- sau đó ta sẽ thay a bằng 3 b = -2x vào
- để thu được a mũ 5 là 3 mũ 5 này tiếp
- theo là 5 nhân với 3 mũ 4 và nhân với
- -2x rồi cộng 10 nhân với 3 mũ 3 nhân với
- trừ 2 bình phương tiếp theo là 10 nhân
- với 3 số 2 và nhân với -2x³ + 5 nhân với
- 3 nhân với -2^4 và cuối cùng là -2x tất
- cả mũ 5 tới đây Chỉ đơn giản là tính
- toán 3 mũ 5 thì bằng 243
- số hạng thứ hai các bạn chú ý dấu của
- chữ 2x này ta được trừ 810x ở đây trừ 2
- tất cả bình thì
- bằng 4x² lên dẫu đây là dấu cộng
- 1.080x^2
- tiếp tới là - 720x^3 +
- 240x^4 và - 32x^5 như vậy ta có khai
- triển của 3 - 2x^5
- và quay trở lại với tam giác Pascal của
- chúng ta nếu thể thay các hệ số trong
- tam giác này bởi các tổ hợp a + b mũ 1
- thầy viết thành
- thì hai hệ số ở hàng thứ Hai hàng hạng 1
- có thể là c01 và C11 tương tự như vậy
- với A + b² và a + b^3 với khai triển như
- thế này thì ta xếp được hệ số tiếp theo
- sẽ là C02 C12 và C22 rồi hãng H3 này
- tiếp theo là hàng H4 và hàng H5 thầy sẽ
- cho khai triển như thế này và các bạn
- cũng sẽ điền được hệ số vào trong tam
- giác với tam giác Pascal thu được đó các
- bạn sẽ để ý c13 và c23 ở đây có 1 + 2 =
- 3
- hay là C14 và c34 cũng có 1 + 3 = 4x
- chúng có mối quan hệ gì với nhau
- ta so sánh được xây 13 thì bằng c23 còn
- C14 thì bằng c34 và tổng quát ckn sẽ
- bằng cn - K của n
- đó là tính chất thứ nhất còn gọi là tính
- chất đối xứng liên quan tới tổ hợp
- Tuy nhận xét đó các bạn sẽ hoàn thành
- cho thấy phép so sánh trong hỏi chấm 3
- chính xác chúng ta sẽ điền thêm vào C15
- là bắn c45 c35 thì bắn C25
- tính chất số 2 còn gọi là hệ thức Pascal
- ta sẽ có ck trừ 1 n - 1 + ckn-1 bằng ckn
- các bạn sẽ chú ý cho thấy hai tính chất
- và các tính chất này thường được sử dụng
- trong các bài toán mà yêu cầu biến đổi
- liên quan tới tổ hợp Ví dụ như hỏi chấm
- 4 tìm số nguyên dương n thỏa mãn C1 2n +
- 1 + C2 hay n + 1 + Vân Vân tới CN hay n
- + 1 bằng 2 mũ 22 trừ 1
- thì để giải quyết hỏi chấm 4 thầy sẽ gợi
- ý cho các bạn thông qua khai triển 1 + 1
- mũ 2 n + 1
- chính xác rồi khai triển này sẽ cho là
- c02n + 1 + C1 hay là cộng 1 cộng vân vân
- tới c2n + 1 hay n + 1 thì thì trong khai
- triển này có tất cả là là 2n + 2 số hạng
- chính xác thì trong khai triển này ta sẽ
- thấy là
- c02n+1 bằng c2n + 1 hay n + 1 Tức là số
- hạng đầu bằng số hạng cuối
- cứ thế số hạng thứ hai thì bằng số hạng
- thứ hai tính từ cuối lên Tức là C1 hayn
- cộng 1 bằng c2n hay n + 1 và cứ như vậy
- ta có CN hay n + 1 = CN + 1 hay n + 1
- Như vậy tổng của chúng ta sẽ chia thành
- hai phần bằng nhau và thầy sẽ tính phần
- từ c0 cho đến CN
- bằng 1 + 1 mũ 2 n + 1 chia 2 1 + 1 thì
- bằng 2 rồi nên ta sẽ có 2 mũ 2n + 1 trên
- 2
- 2 mũ 2n + 1 chính bằng 2 nhân với 2 mũ
- 2n bằng 2 mũ 2n
- Tuy nhiên trong tổng ban đầu của chúng
- ta thì không xuất hiện số hạt c0 hay n +
- 1 nhưng được một kim thuận lợi ở chỗ số
- hạng thứ nhất này bằng 1 cho nên tổng P
- của chúng ta sẽ bằng 2 mũ 2 n trừ đi 1
- và theo giả thiết bằng 2 mũ 22 trừ 1 như
- vậy 2n đây sẽ phải bằng 22 rồi và ta có
- n = 11 là kết quả của hỏi chấm 4

Bạn có thể đánh giá bài học này ở đây