Bài học cùng chủ đề
- Phương pháp quy nạp toán học
- Một số ứng dụng của quy nạp toán học
- Phương pháp quy nạp toán học
- Công thức nhị thức Newton và tam giác Pascal
- Ứng dụng tam giác Pascal trong khai triển nhị thức Newton
- Hệ số trong khai triển nhị thức Newton
- Hệ số trong khai triển nhị thức Newton
- Giải phương trình, hệ phương trình, bất phương trình chứa nhị thức Newton
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
1. Công thức khai triển nhị thức Newton:
Trong khai triển $(a + b)^n$ với $n = 1, 2, 3, 4, 5$ có:
+ $n + 1$ số hạng, trong đó số hạng đầu tiên là $a^n$ và số hạng cuối cùng là $b^n$.
+ tổng số mũ của $a$ và $b$ trong mỗi số hạng đều bằng $n$.
+ số mũ của $a$ giảm 1 đơn vị và số mũ của $b$ tăng 1 đơn vị khi chuyển từ số hạng này đến số hạng tiếp theo (từ trái sang phải).
2. Tam giác Pascal
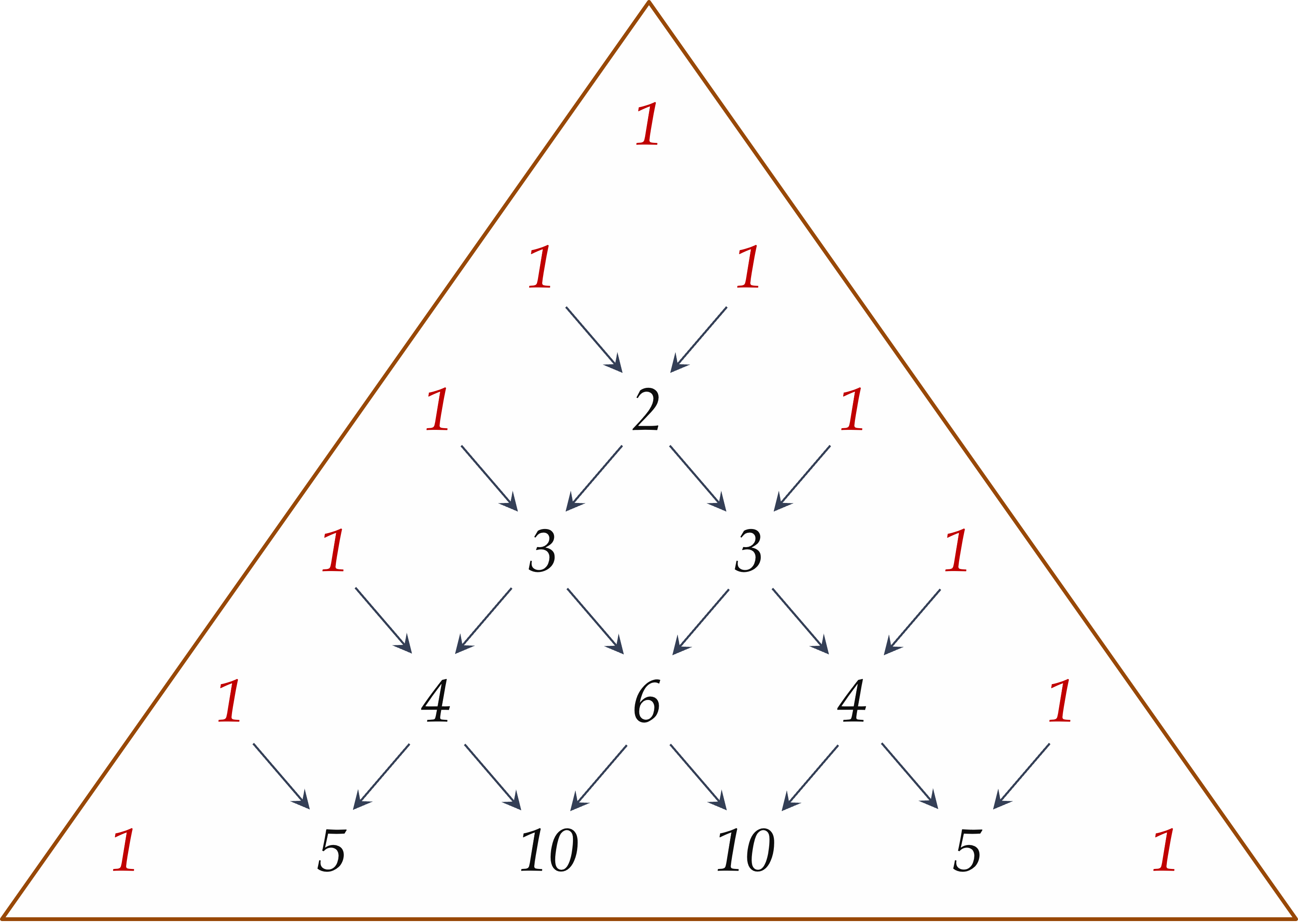
Mọi số khác 1 đều là tổng của hai số ở ngay phía trên nó.
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
Trong mỗi khai triển của (a+b)n với n∈{1;2;3;4;5} có tất cả bao nhiêu số hạng?
n
n−1.
n+1.
Câu 2 (1đ):
Khai triển (a+b)6 (với phần hệ số thay bằng ?) nào sau đây đúng?
A
(a+b)6=a6+?a5b+?a4b2+?a3b3+?a2b4+?ab5+b6.
B
(a+b)6=a6+?a5b+?a4b2+?a3b3+?a2b4+?a5.
C
(a+b)6=a6+?a5b+?a4b2+?a3b3+?a2b4+?a5b+b6.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
OLMc◯2022


Bạn có thể đánh giá bài học này ở đây