Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tự luận (7 điểm) SVIP
(1,5 điểm) Tính bằng cách hợp lí (nếu có thể):
a) $A=2,34+5,35+7,66+4,65$
b) $B=2,13.75+2,13.25$
c) $C=\dfrac{1}{3}-\dfrac{1}{3}: \dfrac{3}{4}$
Hướng dẫn giải:
a) $A=2,34+5,35+7,66+4,65$
$=(2,34+7,66)+(4,65+5,35)$
$=10+10$
$=20$
b) $B=2,13.75+2,13.25$
$=2,13.(75+25)$
$=2,13.100$
$=213$
c) $C=\dfrac{1}{3}-\dfrac{1}{3}: \dfrac{3}{4}$
$=\dfrac{1}{3}-\dfrac{1}{3}. \dfrac{4}{3}$
$=\dfrac{1}{3}-\dfrac{4}{9}$
$=\dfrac{3}{9}-\dfrac{4}{9}$
$=\dfrac{-1}{9}$
(1,5 điểm) Tìm $x$.
a) $\dfrac{1}{2}-\dfrac{1}{2}: x=\dfrac{3}{4}$
b) $\dfrac{x-1}{15}=\dfrac{3}{5}$
c) $x+2,5=1,4$
Hướng dẫn giải:
a) $\dfrac{1}{2}-\dfrac{1}{2}: x=\dfrac{3}{4}$
$\dfrac{1}{2}: x=\dfrac{1}{2}-\dfrac{3}{4}$
$\dfrac{1}{2}: x=\dfrac{-1}{4}$
$x=\dfrac{1}{2}: \dfrac{-1}{4}$
$x=-2$
b) $\dfrac{x-1}{15}=\dfrac{3}{5}$
$\dfrac{x-1}{15}=\dfrac{9}{15}$
$x-1=9$
$x=10$
c) $x+2,5=1,4$
$x=1,4-2,5$
$x=-1,1$
(1,5 điểm) Lớp 6A có $45$ học sinh. Xếp loại học lực gồm: Tốt, Khá, Đạt. Biết học sinh xếp loại Tốt bằng $\dfrac{4}{15}$ học sinh cả lớp. Học sinh xếp loại Khá bằng $\dfrac{5}{3}$ số học sinh xếp loại Tốt. Còn lại là học sinh xếp loại Đạt. Tính số học sinh xếp loại Đạt.
Hướng dẫn giải:
Số học sinh đạt loại Tốt là:
$45.\dfrac{4}{15}=12$ (học sinh)
Số học sinh đạt loại Khá là:
$12.\dfrac{5}{3}=20$ (học sinh)
Số học sinh được xếp loại Đạt là:
$45-12-20=13$ (học sinh)
Đáp số: $13$ học sinh
1.(1 điểm)
Trên tia $Ox$, lấy hai điểm $A$ và $B$ sao cho $A$ là trung điểm của đoạn thẳng $OB$. Biết $OA=2$ cm. Tính $OB$.
2. (1,5 điểm)
Cho hình vẽ
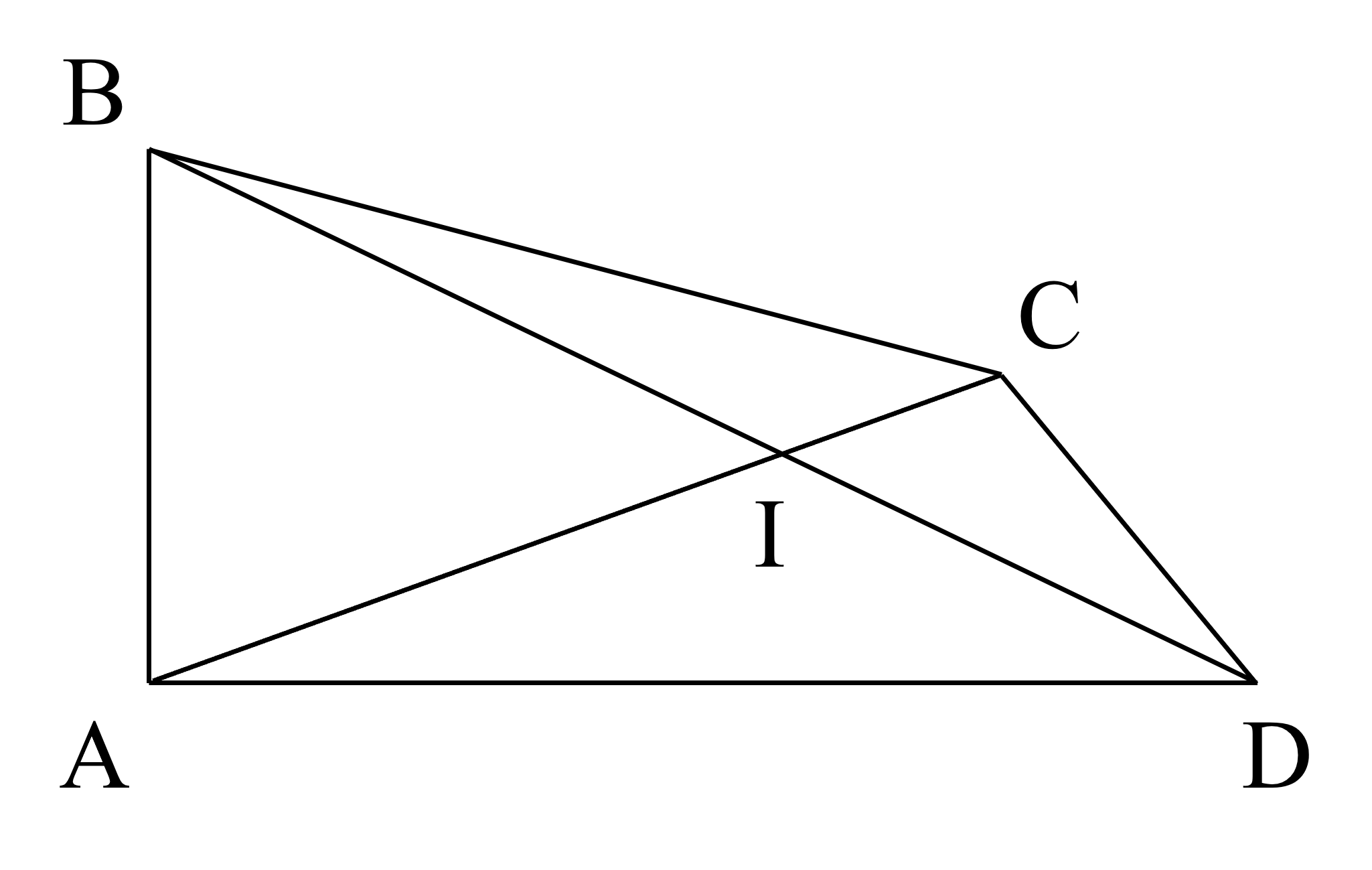
a) Điểm nào nằm trong góc ${BAD}$ ?
b) Chỉ ra một góc bẹt trong hình?
c) Đo và sắp xếp các góc $\widehat{AIC}$ , $\widehat{ACD}$, $\widehat{BCD}$ và $\widehat{BAD}$ theo thứ tự tăng dần về số đo.
Hướng dẫn giải:
1. (Không yêu cầu vẽ hình thật chính xác từng cm).
![]()
Do $A$ là trung điểm $OB$, nên $OB=2.OA$.
Thay số $OA=2$ cm, ta có
$OB=2.2=4$ (cm)
2. (Không yêu cầu vẽ lại hình).

a) Điểm $C$ và điểm $I$ nằm trong góc $BAD$.
b) (Học sinh nêu ra một góc bẹt sẽ đạt điểm tối đa phần này.)
Các góc bẹt trong hình là góc $BID$ và $AIC$.
c) (Không trừ điểm học sinh khi đo góc có sai số từ $1^{\circ}$ đến $2^{\circ}$).
Đo góc, ta lần lượt có các số đo góc như sau:
$\widehat{AIC}=180^{\circ}$
$\widehat{ACD}=70^{\circ}$
$\widehat{BCD}=135^{\circ}$
$\widehat{BAD}=90^{\circ}$
Sắp xếp các góc theo thứ tự tăng dần về số đo, ta được:
$\widehat{ACD};\, \widehat{BAD};\, \widehat{BCD};\, \widehat{AIC}$.
