Tọa độ véctơ SVIP

I. TỌA ĐỘ CỦA MỘT ĐIỂM

Để xác định tọa độ của điểm \(M\) tùy ý trong mặt phẳng tọa độ \(Oxy\) ta làm như sau:

Từ \(M\) kẻ vuông góc với trục hoành và cắt trục hoành tại điểm \(H\) ứng với số \(a\). Số \(a\) là hoành độ điểm \(M\).

Từ \(M\) kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm \(K\) ứng với số \(b\). Số \(b\) là tung độ của điểm \(M.\)

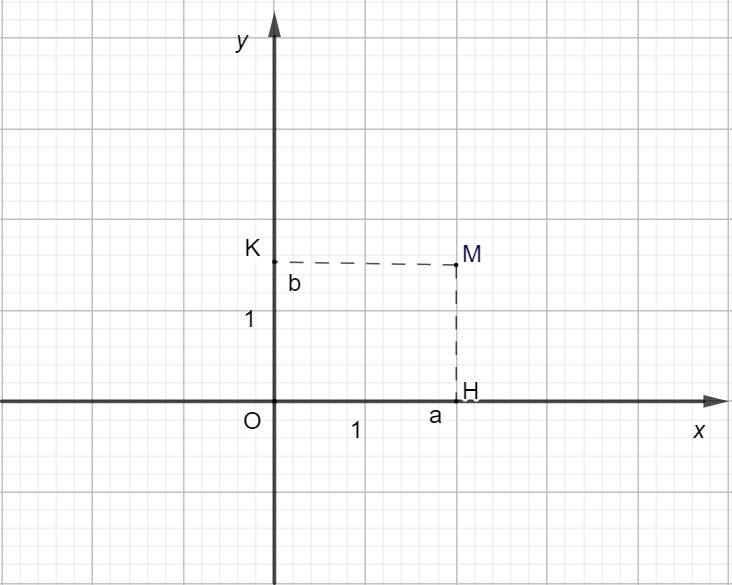
Cặp số \(\left(a;b\right)\) là tọa độ của điểm \(M\) trong mặt phẳng tọa độ \(Oxy\). Kí hiệu là \(M\left(a;b\right)\).

II. TỌA ĐỘ CỦA MỘT VECTƠ

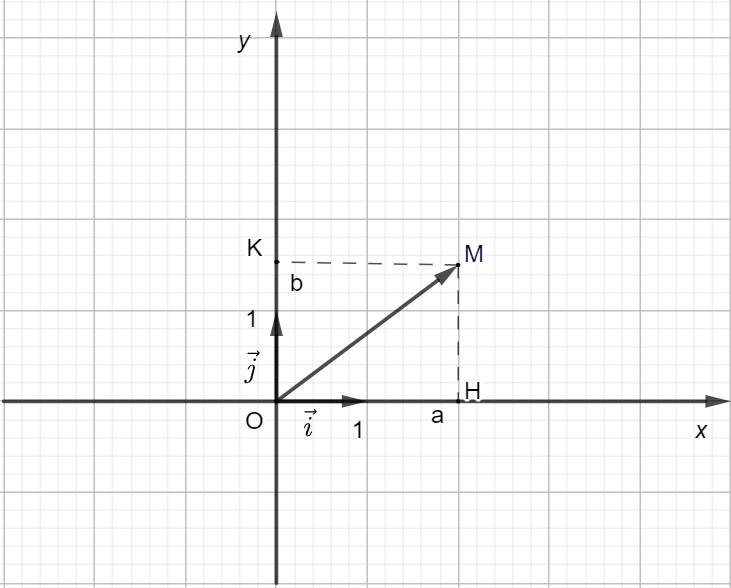
Tọa độ của điểm \(M\) được gọi là tọa độ của vectơ \(\overrightarrow{OM}.\)

Chú ý: Trong mặt phẳng tọa độ \(Oxy\), ta có:

\(\overrightarrow{OM}=\left(a;b\right)\Leftrightarrow M\left(a;b\right).\)

Vectơ \(\overrightarrow{i}\) có điểm gốc là \(O\) và có tọa độ \(\left(1;0\right)\) gọi là vectơ đơn vị trên trục \(Ox\).

Vectơ \(\overrightarrow{j}\) có điểm gốc là \(O\) và có tọa độ \(\left(0;1\right)\) gọi là vectơ đơn vị trên trục \(Oy\).

Nhận xét: Với mỗi vectơ \(\overrightarrow{u}\), ta xác định được duy nhất một điểm \(A\) sao cho \(\overrightarrow{OA}=\overrightarrow{u}.\)

Với mỗi vectơ \(\overrightarrow{u}\) trong mặt phẳng tọa độ \(Oxy\), tọa độ của vectơ \(\overrightarrow{u}\) là tọa độ của điểm \(A\) sao cho \(\overrightarrow{OA}=\overrightarrow{u}.\)

Định lí

Trong mặt phẳng tọa độ \(Oxy\), nếu \(\overrightarrow{u}=\left(a;b\right)\) thì \(\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}\).

Ngược lại nếu \(\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}\) thì \(\overrightarrow{u}=\left(a;b\right)\).

Chú ý: Với \(\overrightarrow{a}\left(x_1;y_1\right);\overrightarrow{b}\left(x_2;y_2\right)\), ta có: \(\overrightarrow{a}=\overrightarrow{b}\Leftrightarrow\left\{{}\begin{matrix}x_1=x_2\\y_1=y_2\end{matrix}\right.\).

Ví dụ: Trong mặt phẳng tọa độ \(Oxy\), cho điểm \(A\left(3;-4\right)\) và vectơ \(\overrightarrow{u}=\left(-2;0\right)\).

a) Biểu diễn vectơ \(\overrightarrow{OA}\) qua hai vectơ \(\overrightarrow{i}\) và \(\overrightarrow{j}\).

b) Biểu diễn vectơ \(\overrightarrow{u}\) qua hai vectơ \(\overrightarrow{i}\) và \(\overrightarrow{j}\).

Giải

a) Vì \(A\left(3;-4\right)\) nên \(\overrightarrow{OA}=\left(3;-4\right)\). Do đó: \(\overrightarrow{OA}=3\overrightarrow{i}-4\overrightarrow{j}.\) 

b) Vì \(\overrightarrow{u}=\left(-2;0\right)\) nên \(\overrightarrow{u}=\left(-2\right)\overrightarrow{i}+0\overrightarrow{j}=-2\overrightarrow{i}.\)

III. LIÊN HỆ GIỮA TỌA ĐỘ ĐIỂM VÀ TỌA ĐỘ VECTƠ

Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(A\left(x_A;y_A\right);B\left(x_B;y_B\right)\); khi đó:

\(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)\).

Ví dụ: Trong mặt phẳng tọa độ \(Oxy\) cho các điểm \(A\left(1;3\right);B\left(-5;1\right);C\left(2;-2\right)\).

a) Tìm tọa độ của vectơ \(\overrightarrow{AB}\).

b) Tìm tọa độ điểm \(D\) sao cho tứ giác \(ABCD\) là hình bình hành.

Giải

a) Ta có \(\overrightarrow{AB}=\left(-5-1;1-3\right)\) nên \(\overrightarrow{AB}=\left(-6;-2\right)\).

b) Gọi tọa độ của điểm \(D\left(x_D;y_D\right)\). Ta có \(\overrightarrow{DC}=\left(2-x_D;-2-y_D\right)\).

Tứ giác \(ABCD\) là hình bình hành khi và chỉ khi \(\overrightarrow{AB}=\overrightarrow{DC}\) hay

\(\overrightarrow{DC}=\left(-6;-2\right)\Leftrightarrow\left\{{}\begin{matrix}2-x_D=-6\\-2-y_D=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_D=8\\y_D=0\end{matrix}\right.\)

Vậy \(D\left(8;0\right)\).