Tập hợp R các số thực SVIP

I. TẬP HỢP SỐ THỰC

1. Số thực

Số hữu tỉ và số vô tỉ được gọi chung là số thực.

Tập hợp các số thực được kí hiệu là \(ℝ\).

2. Biểu diễn thập phân của số thực 

Mỗi số thực là số hữu tỉ hoặc số vô tỉ. Vì thế, mỗi số thực đều biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn.

II. BIỂU DIỄN SỐ THỰC TRÊN TRỤC SỐ

-Tương tự như đối với số hữu tỉ. ta có thể biểu diễn mọi số thực trên trục số, khi đó điểm biểu diễn số thực \(x\) được gọi là điểm \(x\).

-Ta có số \(\sqrt{2}\) được biểu diễn trên trục số thực bằng cách vẽ hình vuông với một cạnh là đoạn thẳng có hai đầu mút là điểm gốc \(0\) và điểm \(1\). Khi đó, ta tính được độ dài đường chéo bằng \(\sqrt{2}.\)

Vẽ đường tròn tâm là gốc \(0\), bán kinh là \(\sqrt{2}.\) Khi đó, đường tròn cắt trục tại điểm nằm bên phải điểm gốc \(0\), thì điểm đó chính là điểm biểu diễn số \(\sqrt{2}\) trên trục số.

Nhận xét

• Do \(\sqrt{2}\) không phải là số hữu tỉ mà là số vô tỉ nên không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ. Vậy các điểm biểu diễn số hữu tỉ không lấp đầy trục số.
• Người ta chứng minh được rằng: Mỗi số thực được biểu diễn bởi một điểm trên trục số; Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.

Vì thế, trục số còn được gọi là trục số thực.

III. SỐ ĐỐI CỦA MỘT SỐ THỰC

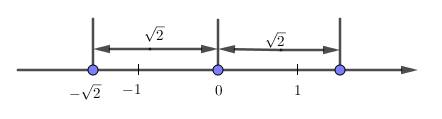
Hai điểm biểu diễn các số thực \(\sqrt{2}\) và \(-\sqrt{2}\) nằm về hai phía của điểm gốc \(0\) và cách đều điểm gốc \(0\)

Trên trục số, hai số thực (phân biệt) có điểm biểu diễn nằm về hai phía của điểm gốc \(0\) và cách đều điểm gốc \(0\) được gọi là hai số đối nhau.

Số đối của số thực \(a\) kí hiệu là \(-a\).

Số đối của số \(0\) là \(0.\)

Nhận xét: Số đối của số \(-a\)  là số \(a\), tức là \(-\left(-a\right)=a.\)

IV. SO SÁNH CÁC SỐ THỰC

1. So sánh hai số thực

Cũng như số hữu tỉ, trong hai số thữ khác nhau luôn có một số nhỏ hơn số kia.

• Nếu số thực \(a\) nhỏ hơn số thực \(b\) thì ta viết \(a< b\) hay \(b>a.\)
• Số thực lớn hơn \(0\) được gọi là số thực dương.
• Số thực nhỏ hơn \(0\) được gọi là số thực âm.
• Số \(0\) không phải là số thực dương cũng không phải số thực âm.
• Nếu \(a< b\) và \(b< c\) thì \(a< c.\)

2. Cách so sánh hai số thực

Trong những trường hợp thuận lợi, ta có thể so sánh hai số thực bằng cách biểu diễn thập phân mỗi số thực đó rồi so sánh hai số thập phân đó.

Chú ý: Với \(a,b\) là hai số thực dương, nếu \(a>b\) thì \(\sqrt{a}>\sqrt{b}.\)

3. Minh hoạ trên trục số

Giả sử hai điểm \(x,y\) lần lượt biểu diễn hai số thực \(x,y\) trên trục số nằm ngang, ta có:

-Nếu \(x< y\) hay \(y>x\) thì điểm \(x\) nằm bên trái điểm \(y\);

-Ngược lại, nếu điểm \(x\) nằm bên trái điểm \(y\) thì  \(x< y\) hay \(y>x\) .

Đối với hai điểm \(x,y\) lần lượt biểu diễn hai số thực \(x,y\) trên trục số thẳng đứng, ta có:

-Nếu \(x< y\) hay \(y>x\) thì điểm \(x\) nằm phía dưới điểm \(y\);

-Ngược lại, nếu điểm \(x\) nằm phía dưới điểm \(y\) thì  \(x< y\) hay \(y>x\) .