Quy tắc đếm SVIP

1. QUY TẮC CỘNG VÀ SƠ ĐỒ HÌNH CÂY

Quy tắc cộng

Giả sử có một công việc nào đó có thể thực hiện theo một trong hai phương án khác nhau:

- Phương án một có \(n_1\) cách thực hiện,

- Phương án hai có \(n_2\) cách thực hiện.

Khi đó số cách thực hiện công việc sẽ là: \(n_1+n_2\) cách.

Chú ý.

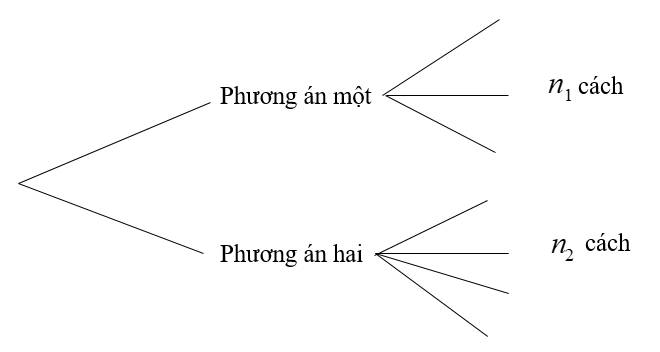
Sơ đồ minh họa như trên được gọi là sơ đồ hình cây. Trong các bài toán đếm, sơ đồ hình cây giúp cho việc đếm thuận tiện và không bỏ sót trường hợp.

Chú ý. Ta áp dụng quy tắc cộng cho một công việc có nhiều phương án khi các phương án đó phải rời nhau, không phụ thuộc vào nhau (độc lập với nhau).

Ví dụ. Lớp \(10\)A có \(40\) học sinh, lớp \(10\)B có \(38\) học sinh. Có bao nhiêu cách cử một học sinh của lớp \(10\)A hoặc của lớp \(10\)B tham gia buổi giao lưu các học sinh trong các trường trung học phổ thông trong tỉnh sắp diễn ra?

Giải

Ta có thể minh họa bằng sơ đồ hình cây

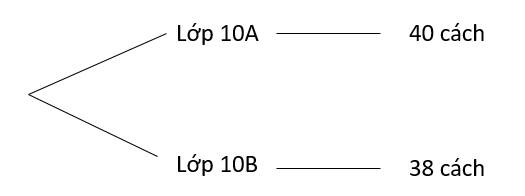
Công việc cử một học sinh có hai phương án lựa chọn:

Phương án một: cử một học sinh của lớp \(10\)A có \(40\) cách thực hiện.

Phương án hai: cử một học sinh của lớp \(10\)B có \(38\) cách thực hiện.

Theo quy tắc cộng có \(40+38=78\) cách chọn một học sinh tham gia buổi giao lưu các học sinh trong các trường trung học phổ thông trong tỉnh.

2. QUY TẮC NHÂN

Giả sử một công việc nào đó phải hoàn thành qua hai công đoạn liên tiếp nhau:

- Công đoạn một có \(m_1\) cách thực hiện,

- Với mỗi cách thực hiện công đoạn một có \(m_2\) cách thực hiện công đoạn hai.

Khi đó số cách thực hiện công việc là \(m_1.m_2\) cách.

Chú ý. Quy tắc nhân áp dụng để tính số cách thực hiện một công việc có nhiều công đoạn, các công đoạn nối tiếp nhau và những công đoạn này độc lập với nhau.

Ví dụ. Lan có \(5\) chiếc áo và \(3\) chiếc quần. Lan có bao nhiêu cách lựa chọn một bộ quần áo để mặc đi chơi.

Giải

Việc chọn một bộ quần áo của Lan có thể coi như là hai công đoạn:

Công đoạn \(1\): chọn một chiếc áo từ \(5\) chiếc áo, có \(5\) cách thực hiện công đoạn này.

Công đoạn \(2\): chọn một chiếc quần từ \(3\) chiếc quần, có \(3\) cách thực hiện công đoạn này.

Áp dụng quy tắc nhân, có \(5.3=15\) cách lựa chọn một bộ quần áo để mặc đi chơi.

3. KẾT HỢP QUY TẮC CỘNG VÀ QUY TẮC NHÂN

Ví dụ. Từ các số \(0,1,2,3,4\) có thể lập được bao nhiêu:

a) số tự nhiên có \(4\) chữ số khác nhau?

b) số tự nhiên chẵn có \(4\) chữ số khác nhau?

Giải

Gọi số cần lập là \(\overline{abcd}\) với \(a,b,c,d\) là bốn chữ số khác nhau từ các chữ số đã cho.

a) Có \(4\) cách chọn chữ số \(a\) từ \(4\) chữ số khác \(0\) đã cho.

Với mỗi cách chọn \(a\), có \(4\) cách chọn chữ số \(b\) từ \(4\) chữ số còn lại.

Ứng với mỗi cách chọn \(b\) đó, có \(3\) cách chọn chữ số \(c\) từ \(3\) chữ số còn lại.

Ứng với mỗi cách chọn \(c\) đó, có \(2\) cách chọn chữ số \(d\) từ \(2\) chữ số còn lại.

Áp dụng quy tắc nhân có: \(4.4.3.2=96\) số tự nhiên có \(4\) chữ số khác nhau được lập từ các số đã cho.

b) Để \(\overline{abcd}\) là số chẵn, chữ số \(d\) phải là chữ số chẵn. Vậy có hai trường hợp:

Trường hợp \(1:\)\(d=0\) khi đó có \(4\) cách chọn chữ số \(a\) từ \(4\) chữ số còn lại, ứng với mỗi cách chọn \(a\) đó có \(3\) cách chọn chữ số \(b\) từ \(3\) chữ số còn lại. Với mỗi cách chọn \(b\), có \(2\) cách chọn chữ số \(c\) từ \(2\) chữ số còn lại.

Áp dụng quy tắc nhân có: \(4.3.2=24\) số thỏa mãn.

Trường hợp \(2:\)\(d=2\) hoặc \(d=4\).

Khi đó có \(2\) cách chọn chữ số \(d\) từ \(2\) chữ số \(2\) hoặc \(4\). Với mỗi cách chọn đó có \(3\) cách chọn chữ số \(a\) từ \(3\) chữ số khác \(0\) còn lại. Với mỗi cách chọn \(a\), có \(3\) cách chọn chữ số \(b\) từ \(3\) chữ số còn lại, Với mỗi cách chọn \(b\), có \(2\) cách chọn chữ số \(c\) từ \(2\) chữ số còn lại.

Áp dụng quy tắc nhân có: \(2.3.3.2=36\) số thỏa mãn.

Theo quy tắc cộng có: \(24+36=60\) số chẵn có \(4\) chữ số khác nhau thỏa mãn.​