Phần tự luận (8 điểm) SVIP

Hướng dẫn giải:

a) $A=4\sqrt{20}-3\sqrt{125}+5\sqrt{45}-15\sqrt{\dfrac{1}{5}}$

 $ =4.2\sqrt{5}-3.5\sqrt{5}+5.3\sqrt{5}-3\sqrt{\dfrac{25}{5}} $

 $ =8\sqrt{5}-15\sqrt{5}-3\sqrt{5}+15\sqrt{5} $

 $ =5\sqrt{5} $.

b)  $B=\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}$

$ =\sqrt{5}-\sqrt{3-\sqrt{(\sqrt{20}-3)^2}} $

$ =\sqrt{5}-\sqrt{3-(\sqrt{20}-3)} $

$ =\sqrt{5}-\sqrt{6-\sqrt{20}} $

$ =\sqrt{5}-\sqrt{(\sqrt{5}-1)^2} $

$ =\sqrt{5}-(\sqrt{5}-1) $

$ =1 $.

Hướng dẫn giải:

a)

Với  $a>0,a\ne 1$, ta có:

$P=\dfrac{\sqrt{a}(\sqrt{a^3}-1)}{a+\sqrt{a}+1}-\dfrac{\sqrt{a}(2\sqrt{a}+1)}{\sqrt{a}}+\dfrac{2(\sqrt{a}-1)(\sqrt{a}+1)}{\sqrt{a}-1}$

$P=\dfrac{\sqrt{a}(\sqrt{a}-1)(a+\sqrt{a}+1)}{a+\sqrt{a}+1}-(2\sqrt{a}+1)+2(\sqrt{a}+1)$

$P=\sqrt{a}(\sqrt{a}-1)+1$

$P=a-\sqrt{a}+1$.

b)

$P=a-\sqrt{a}+1=\Big( \sqrt{a}-\dfrac{1}{2} \Big)^2+\dfrac{3}{4}\ge \dfrac{3}{4}$ (Với $\forall a>0,a\ne 1$)

Vậy giá trị nhỏ nhất của $P=\dfrac{3}{4}$ khi $a=\dfrac{1}{4}$.

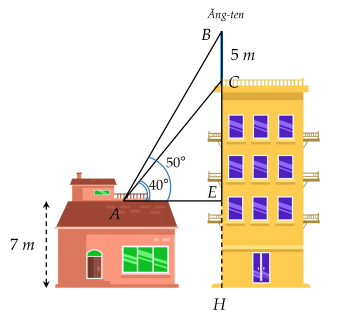
Hướng dẫn giải:

Dựa vào hình vẽ bài toán, ta có:

$BC = 5$ m

$EH = 7$ m

$\widehat{BAE}=50^\circ; \widehat{CAE}=40^\circ$

$\widehat{CEA}=\widehat{BEA}=90^\circ$

Xét $\Delta CAE$ vuông tại $E$, ta có:

$\tan \widehat{CAE} =\dfrac{CE}{AE}$ (tỉ số lượng giác của góc nhọn)

Suy ra $ CE=AE.\tan\widehat{CAE} =AE\tan40^\circ\,$ (m) (1)

Xét $\Delta BAE$ vuông tại $E$, ta có:

$\tan \widehat{BAE}=\dfrac{BE}{AE}$ (tỉ số lượng giác của góc nhọn)

$\Rightarrow BE=AE.\tan\widehat{BAE}=AE.\tan 50^\circ\,$ (m) (2)

Từ (1) và (2) suy ra

$BE-CE=AE.\tan 50^\circ-AE.\tan40^\circ$

$BC=AE.(\tan50^\circ-\tan40^\circ) $

$ 5=AE.(\tan50^\circ-\tan40^\circ) $

$ AE=\dfrac{5}{\tan50^\circ-\tan40^\circ} $ (m)

Từ (1) suy ra $CE=\dfrac{5}{\tan50^\circ-\tan40^\circ}.\tan40^\circ$ (m)

$BH=BC+CE+EH=5+\dfrac{5.\tan40^\circ}{\tan50^\circ-\tan40^\circ}+7\approx 23,9 $ m.

Vậy chiều cao của tòa nhà là $23,9$ m.

Hướng dẫn giải:

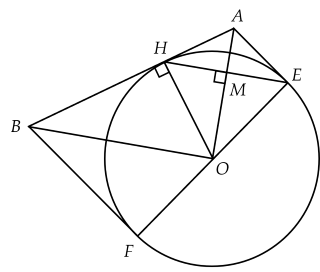
a) Xét $\Delta OHE$ cân tại $O$ ($OH=OE =R$) có $OM$ là đường cao nên đồng thời là đường trung tuyến.

Suy ra $M$ là trung điểm của $EH$, hay $EH = 2EM$.

Áp dụng định lý Pythagore cho tam giác vuông $OME$, có:

$EM = \sqrt{OE^2 - OM^2} = \sqrt{5^2 - 3^2} = 4$ (cm)

Vậy $EH = 2EM = 8$ (cm).

b) Xét $\Delta AHM$ và $\Delta AEM$ có

$ME = MH$ (giả thiết);

$\widehat{AMH} = \widehat{AME}=90^\circ$;

$AM$: cạnh chung.

Do đó,  $\Delta AHM = \Delta AEM$ (c-g-c)

Suy ra: $AE = AH$ (hai cạnh tương ứng)

Xét hai tam giác $OEA$ và tam giác $OHM$, có:

+ $OE = OH (= R)$;

+ $AE = AH$;

+ $OA$ chung.

Nên $\Delta OEA = \Delta OHA$ (c-c-c)

Suy ra: $\widehat{AOH} = \widehat{OEA} = 90^\circ$.

Hay $AH \perp OH$, vậy $AH$ là tiếp tuyến của đường tròn tâm $O$.

c) Có $OH \perp AH$, hay $B$ là giao của hai tiếp tuyến $BH; BF$.

Vậy, $\widehat{BOF} = \widehat{BOH}$, lại có $\widehat{EOA} = \widehat{HOA}$, nên:

$\widehat{EOA} + \widehat{AOB} + \widehat{BOF} = 2(\widehat{ AOH} + \widehat{BOH}) = 2\widehat{AOB} = 180^\circ.$

Tức là $E, O, F$ thẳng hàng. 

$\widehat{AOE} + \widehat{BOF} = 90^\circ$

Suy ra $\widehat{OAE} = \widehat{BOF}$ cùng phụ $\widehat{AOE}.$

Suy ra: $\Delta AOE \sim \Delta OBF$ (g-g)

Tức là: $\dfrac{AE}{OF} = \dfrac{OE}{BF}$

Vậy $AE . BF = OE . OF = R^2.$

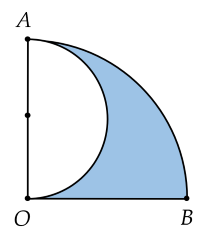
Hướng dẫn giải:

Diện tích nửa hình tròn đường kính $4$ cm phần trắng là: $S_1=\dfrac{1}{2}.\pi .R^2=\dfrac{1}{2}.\pi .2^2=2\pi $ cm$^2$ .

Diện tích hình quạt $AOB$ là: ${{S}_{2}}=\dfrac{1}{4}.\pi.{R_2}^2=\dfrac{1}{4}.\pi .4^2=4\pi $ cm$^2$ .

Diện tích phần tô màu là: $S=S_2-S_1=4\pi -2\pi =2\pi$ cm$^2$ .

Hướng dẫn giải:

Đặt $y = 3 - x$, bài toán đã cho trở thành: Tìm giá trị nhỏ nhất của biểu thức $P=x^4+y^4+6x^2y^2$ với $x, y$ là hai số thực thay đổi thỏa mãn $\left\{ \begin{aligned} & x^2+y^2\ge 5 \\  & x+y=3 \end{aligned} \right.$

Ta có : $\left\{ \begin{aligned}  & x^2+y^2\ge 5 \\  & x+y=3 \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}  & x^2+y^2\ge 5 \\  & x^2+2xy+y^2=9 \end{aligned} \right.$

Suy ra $x^2+y^2+4(x^2+2xy+y^2) \ge 5+4.9=41 \Rightarrow 5(x^2+y^2)+4.2xy\ge 41$

Ta có : $16(x^2+y^2)^2+25(2xy)^2\ge 40 (x^2+y^2)(2xy)$           (1)

Dấu "$=$" xảy ra khi $4(x^2+y^2)=5(2xy)$

Cộng hai vế của (1) với $25(x^2+y^2)^2+16(2xy)^2$ ta được :

$(x^2+y^2)^2+41(2xy)^2\ge \left[ 5(x^2+y^2)+4(2xy) \right]^2 \ge 41^2 $

$(x^2+y^2)^2+4x^2 y^2 \ge 41$

$x^4+y^4+6x^2y^2\ge 41$

Dấu "$=$" xảy ra khi: $\left\{ \begin{aligned}   &x^2+y^2=5 \\  & x+y=3 \\  & 4(x^2+y^2)=5(2xy) \end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}  & x=1,y=2 \\& x=2,y=1 \end{aligned} \right.$

Vậy giá trị nhỏ nhất của $P$ là $41$ khi $x = 1, y = 2$ hoặc $x = 2, y = 1$.