Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (8 điểm) SVIP
Bài 1. (1,0 điểm) Giải các phương trình sau:
a) $3x-5=4$.
b) $\dfrac{2x}{3}+\dfrac{3x-1}{6}=\dfrac{x}{2}$.
Hướng dẫn giải:
a) $3x-5=4$
$3x=9$
$x=3$
Vậy phương trình có nghiệm $x=3$.
b) $\dfrac{2x}{3}+\dfrac{3x-1}{6}=\dfrac{x}{2}$
$\dfrac{4x}{6}+\dfrac{3x-1}{6}=\dfrac{3x}{6}$
$4x+3x-1=3x$
$4x=1$
$x=\dfrac{1}{4}$
Vậy phương trình có nghiệm $x=\dfrac{1}{4}$.
Bài 2. (2,0 điểm) Một người đi xe máy từ thành phố về quê với vận tốc trung bình $30$ km/h. Lúc lên thành phố người đó đi với vận tốc là $25$ km/h. Nên thời gian lúc lên thành phố nhiều hơn thời gian về quê là $20$ phút. Tính quãng đường từ thành phố về quê.
Hướng dẫn giải:
Đổi $20$ phút $=\dfrac{1}{3}$ h.
Gọi $x$ là độ dài quãng đường từ thành phố về quê.
Điều kiện $x>0$; đơn vị: km.
Thời gian người đó đi từ thành phố về quê là: $\dfrac{x}{30}$ km/h.
Thời gian người đó đi từ quê lên thành phố là: $\dfrac{x}{25}$ km/h.
Vì thời gian lúc lên thành phố nhiều hơn thời gian về quê là $20$ phút nên ta có phương trình:
$\dfrac{x}{25}=\dfrac{x}{30}+\dfrac13$
$\dfrac{5x}{750} = \dfrac13$
$15x = 750$
$x = 50$ (thỏa mãn).
Vậy độ dài quãng đường từ thành phố về quê là $50$ km.
Bài 3. (2,0 điểm)
a) Vẽ đồ thị hàm số $y=2mx+1$ với $m=-1$.
b) Tìm $a$, $b$ để đường thẳng $\left(d\right): \, y=ax+b$ đi qua $A\left( 1;-8 \right)$ và song song với đường thẳng $\left(d'\right): \, y=-3x+9$.
Hướng dẫn giải:
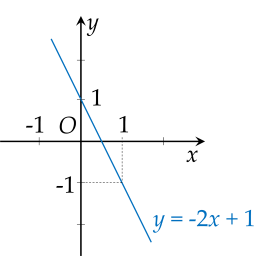
a) Với $m=-1$, hàm số trở thành $y=-2x+1$.
Xét hàm số $y=-2x+1$ :
Thay $x=0$ thì $y=1$.
Suy ra đồ thị hàm số $y=-2x+1$ đi qua điểm có tọa độ $\left( 0;1 \right)$.
Thay $x=1$ thì $y=-1$.
Suy ra đồ thị hàm số $y=-2x+1$ đi qua điểm có tọa độ $\left( 1;-1 \right)$.
Vẽ đồ thị:
b) Vì đường thẳng $\left( d \right): \, y=ax+b$ song song với đường thẳng $\left(d' \right): \, y=-3x+9$ nên: $a\ne -3; \, b\ne 9$.
Khi đó ta có: $\left( d \right): \, y=-3x+b$ và $b\ne 9$.
Vì đường thẳng $\left( d \right): \, y=ax+b$ đi qua $A\left( 1;-8 \right)$ nên: $-8=-3.1+b$
Suy ra $b=-5$ (thoả mãn)
Vậy đường thẳng cần tìm là $\left( d \right): \, y=-3x-5$.
Bài 4. (2,5 điểm) Cho tam giác $ABC$ nhọn $(AB<AC)$, ba đường cao $AD, \, BE, \, CF$ cắt nhau tại $H$.
a) Chứng minh tam giác $ABE$ đồng dạng với tam giác $ACF$. Từ đó suy ra $AB.AF=AC.AE$.
b) Chứng minh $\widehat{AFE}=\widehat{ACB}$.
c) Đường thẳng $EF$ cắt $AD$ và tia $CB$ lần lượt tại $I$ và $K$. Chứng minh $\dfrac{KF}{KE}=\dfrac{IF}{IE}$.
Hướng dẫn giải:
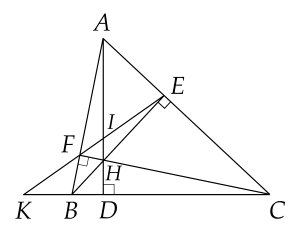
a) Xét $\Delta {ABE}$ và $\Delta {ACF}$ có:
$\widehat{BAC}$ chung;
$\widehat{AEB}=\widehat{AFC}={{90}^{\circ }}$;
Do đó $\Delta {ABE}\backsim \Delta {ACF}$ (g.g).
Suy ra $\dfrac{AB}{AC}=\dfrac{AE}{AF}$ nên $AB.AF=AC.AE$.
b) Từ $AB.AF=AC.AE$ suy ra $\dfrac{AE}{AF}=\dfrac{AB}{AC}$.
Xét $\Delta {AEF}$ và $\Delta {ABC}$ có:
$\dfrac{AE}{AF}=\dfrac{AB}{AC}$ (cmt);
$\widehat{BAC}$ chung;
Do đó $\Delta {AEF}\backsim \Delta {ABC}$ (c.g.c)
Suy ra $\widehat{AFE}=\widehat{ACB}$ (cặp góc tương ứng).
c) Xét $\Delta {CEB}$ và $\Delta {CDA}$ có:
$\widehat{ACB}$ chung;
$\widehat{CEB}=\widehat{CDA}={{90}^{\circ }}$
Do đó $\Delta {CEB}\backsim \Delta {CDA}$ (g.g)
Suy ra $\dfrac{CB}{CE}=\dfrac{CA}{CD}$ (cặp cạnh tương ứng).
Xét $\Delta {CBA}$ và $\Delta {CED}$ có:
$\dfrac{CB}{CE}=\dfrac{CA}{CD}$ (cmt);
$\widehat{ACB}$ chung;
Do đó $\Delta {CBA} \backsim \Delta {CED}$ (c.g.c)
Suy ra $\widehat{CDE}=\widehat{CAB}$ (cặp góc tương ứng) (1)
Tương tự: $\widehat{BDF}=\widehat{CAB}$ (2).
Từ (1) và (2) suy ra $\widehat{CDE}=\widehat{BDF}$.
Mà $\widehat{CDE}+\widehat{EDA}=\widehat{BDF}+\widehat{FDA}$ suy ra $\widehat{EDA}=\widehat{FDA}$.
Suy ra $DA$ là phân giác của góc $EDF$.
Mặt khác $AD\perp KD$ nên $DK$ là phân giác ngoài của $\Delta DEF$.
Ta có $DI$ là phân giác trong của $\Delta DEF$ suy ra $\dfrac{IF}{IE}=\dfrac{DF}{DE}$ (3)
Ta có $DK$ là phân giác ngoài của $\Delta DEF$ suy ra $\dfrac{KF}{KE}=\dfrac{DF}{DE}$ (4)
Từ (3) và (4) suy ra $\dfrac{IF}{IE}=\dfrac{KF}{KE}$.
Bài 5. (0,5 điểm) Giải phương trình ẩn $x$: $\dfrac{x-a}{bc}+\dfrac{x-b}{ca}+\dfrac{x-c}{ab}=\dfrac{2}{a}+\dfrac{2}{b}+\dfrac{2}{c}$ với $a, \, b, \, c \in \mathbb{R}$.
Hướng dẫn giải:
Ta có: $\dfrac{x-a}{bc}+\dfrac{x-b}{ca}+\dfrac{x-c}{ab}=\dfrac{2}{a}+\dfrac{2}{b}+\dfrac{2}{c}$
$\left( \dfrac{x-a}{bc}-\dfrac{2}{a} \right)+\left( \dfrac{x-b}{ca}-\dfrac{2}{b} \right)+\left( \dfrac{x-c}{ab}-\dfrac{2}{c} \right)=0$
$\dfrac{a\left( x-a \right)-2bc+b\left( x-b \right)-2ca+c\left( x-c \right)-2ab}{abc}=0$
Điều kiện xác định: $a,b,c\ne 0$
Khi đó: $\dfrac{\left( a+b+c \right)x-{{a}^{2}}-2bc-{{b}^{2}}-2ca-{{c}^{2}}-2ab}{abc}=0$
$\left( a+b+c \right)x={{(a+b+c)}^{2}}$
+ Nếu $a+b+c=0$ thì phương trình có vô số nghiệm.
+ Nếu $a+b+c\ne 0$ thì phương trình có nghiệm duy nhất $x=a+b+c$.
