Phần tự luận (8 điểm) SVIP

Hướng dẫn giải:

a) $7x + 2 = 0$

$7x = -2$

$x = -\dfrac27$.

b) $18 - 5x = 7 + 3x$

$-5x - 3x = 7 - 18$

$-8x = -11$

$x = \dfrac{11}8$.

Hướng dẫn giải:

a) Rút gọn $A=\dfrac{(x-1)^2}{(x-1)(x+1)}=\dfrac{x-1}{x+1}$.

b) Với $x=3$ thì $A=\dfrac{3-1}{3+1}=\dfrac{1}{2}$

Với $x=\dfrac{3}{2}$ thì $A=\dfrac{-\dfrac{3}{2}-1}{-\dfrac{3}{2}+1}=5$

c) Ta có biến đối: $A=\dfrac{x-1}{x+1}=1+\dfrac{-2}{x+1}$.

Để biểu thức $A$ nguyên khi $\dfrac{-2}{x+1}$ hay $x+1$ là ước của $-2$.

Do đó

Đối chiếu điều kiện ta thấy $x$ có giá trị $-2; \, -3; \, 0$ thì biểu thức $A$ nguyên.

Hướng dẫn giải:

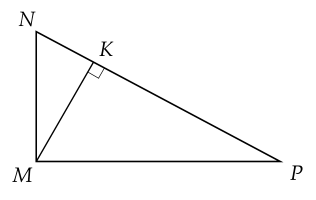
a) Xét $\Delta KNM$ và $\Delta MNP$ có:

     $\widehat{MKN}=\widehat{NMP}=90^\circ$;

     $\widehat{N}$ chung;

Suy ra $\Delta KNM\backsim\Delta MNP$ (g.g) (1)

Xét $\Delta KMP$ và $\Delta MNP$ có:

     $\widehat{MKP}=\widehat{NMP}=90^\circ$

    $\widehat{P}$ là góc chung

Do đó $\Delta KMP\backsim\Delta MNP$ (g.g) (2)

Từ (1) và (2) suy ra $\Delta K N M \backsim \Delta K M P$.

b) Theo câu a $\Delta K N M \backsim \Delta K M P$.

Từ đây ta có tỉ lệ thức: $\dfrac{M K}{K P}=\dfrac{N K}{M K}$

Nên $M K . M K=N K . K P$ hay $M K^2=N K . K P$

c) Từ câu b, ta tính được $MK=6$ cm.

Nên $S_{MNP}=\dfrac{1}{2}MK . NP=\dfrac{1}{2} . 6 . (4+9)=39$ cm$^2$.

Hướng dẫn giải:

Ta có $x^2-4 x+9=(x-2)^2+5 \geqslant 5$.

Suy ra $B=\dfrac{1}{x^2-4 x+9}=\dfrac{1}{(x-2)^2+5} \leqslant \dfrac{1}{5}$.

Dấu bằng xảy ra khi $x=2$.