Một số khái niệm và các tính chất được thừa nhận SVIP

I. Mặt phẳng trong không gian

Mặt phẳng trong không gian không có bề dày và không có giới hạn.

1) Biểu diễn mặt phẳng:

- Để biểu diễn mặt phẳng, ta có thể sử dụng hình bình hành hoặc một góc. 

- Để kí hiệu mặt phẳng, ta dùng chữ cái in hoa hay chữ cái Hy-lạp ở trong dấu ngoặc.

 Mặt phẳng $(P)$.

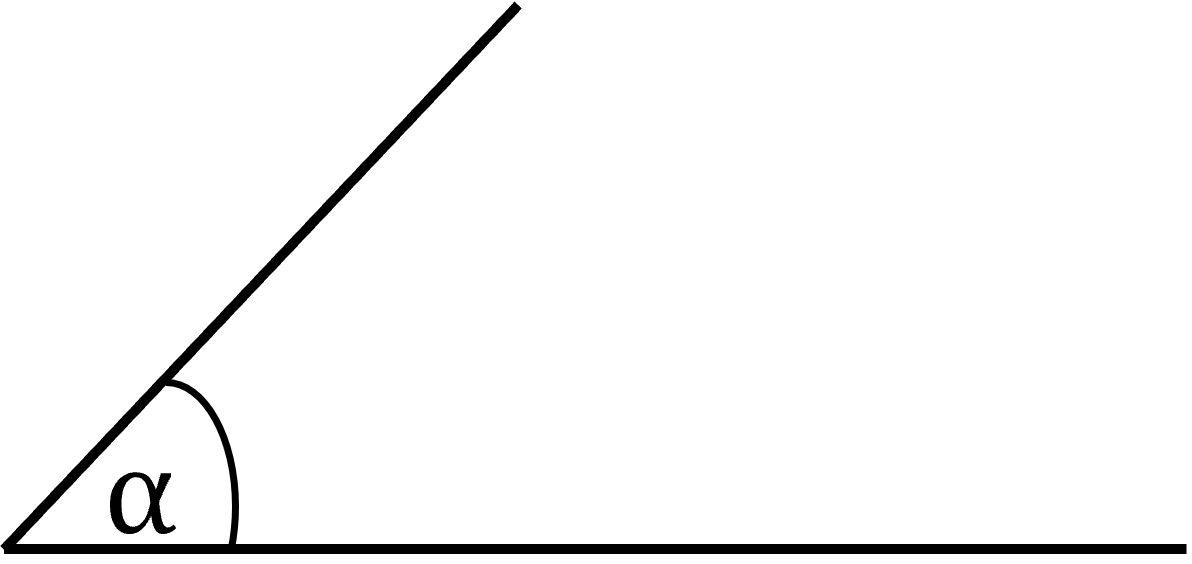 Mặt phẳng ($\alpha$).

2) Điểm và mặt phẳng:

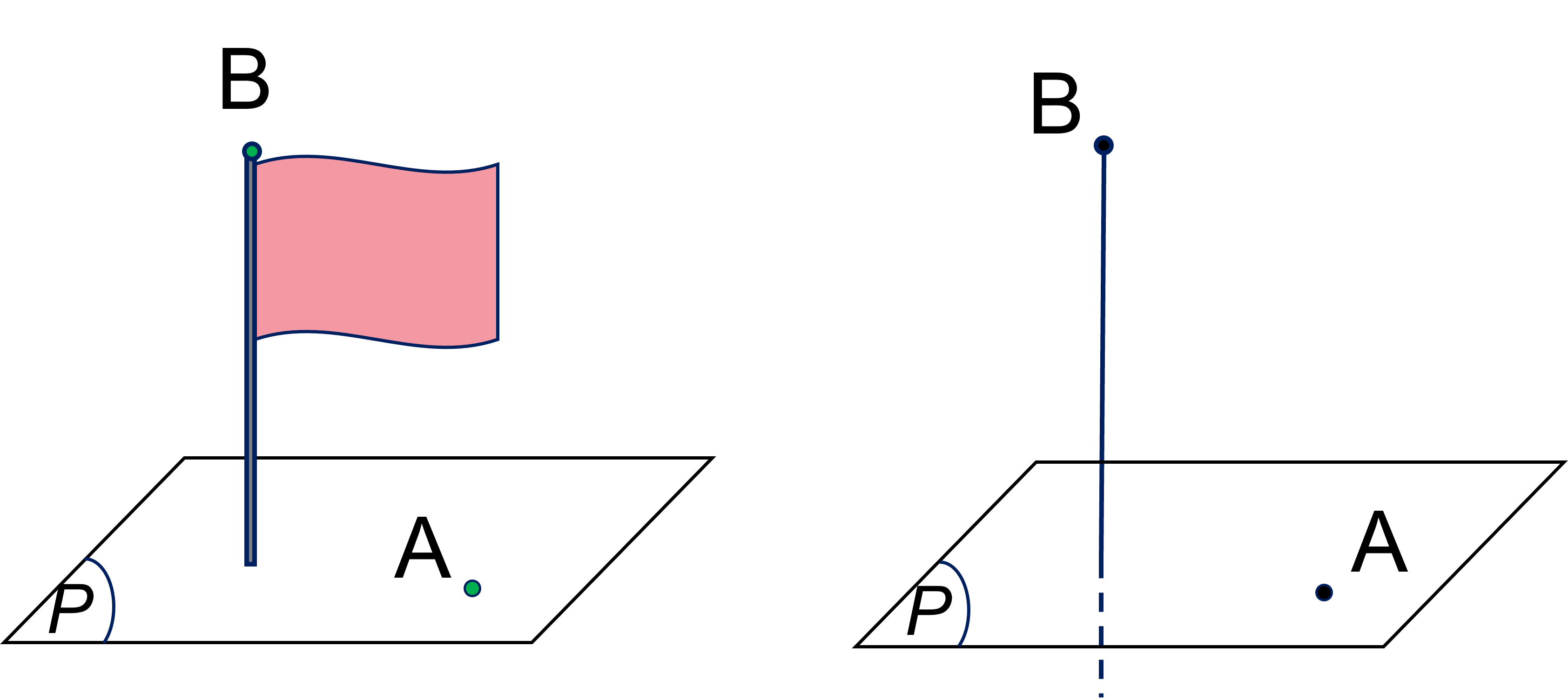
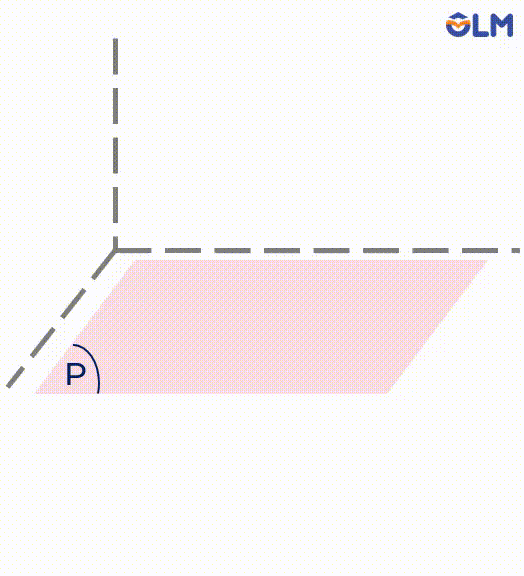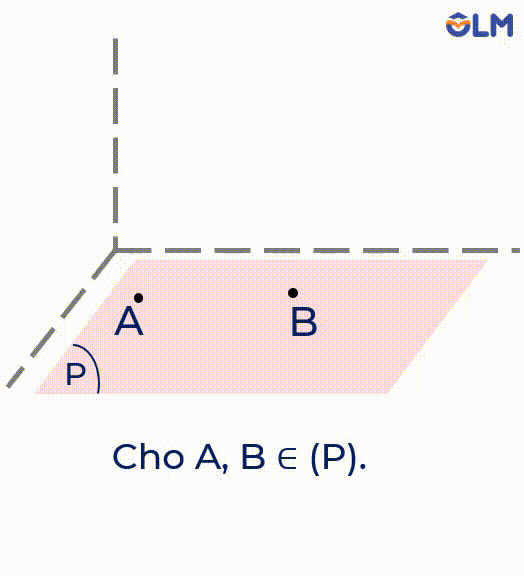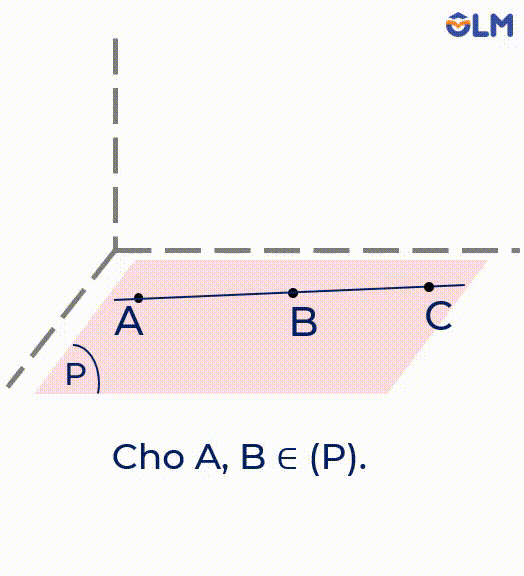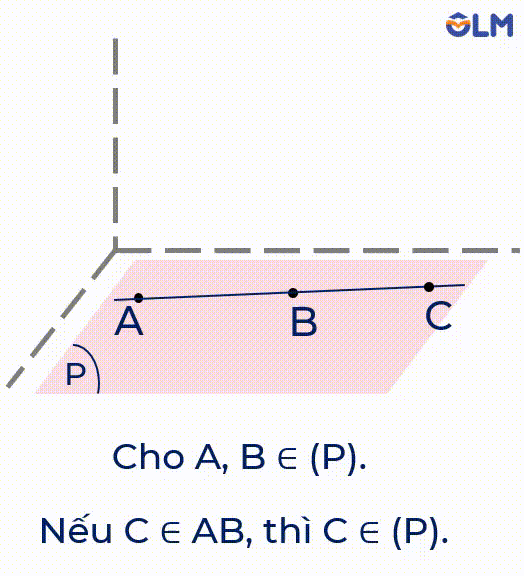
- Điểm $A$ thuộc mặt phẳng $(P)$, kí hiệu $A \in (P)$.

- Điểm $B$ không thuộc mặt phẳng $(P)$, kí hiệu $B \notin (P)$.

3) Hình biểu diễn của một hình không gian:

⚡ Quy tắc vẽ hình biểu diễn của một hình trong không gian (3 chiều) lên mặt phẳng giấy (2 chiều):

- Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng. 

- Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau.

- Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.

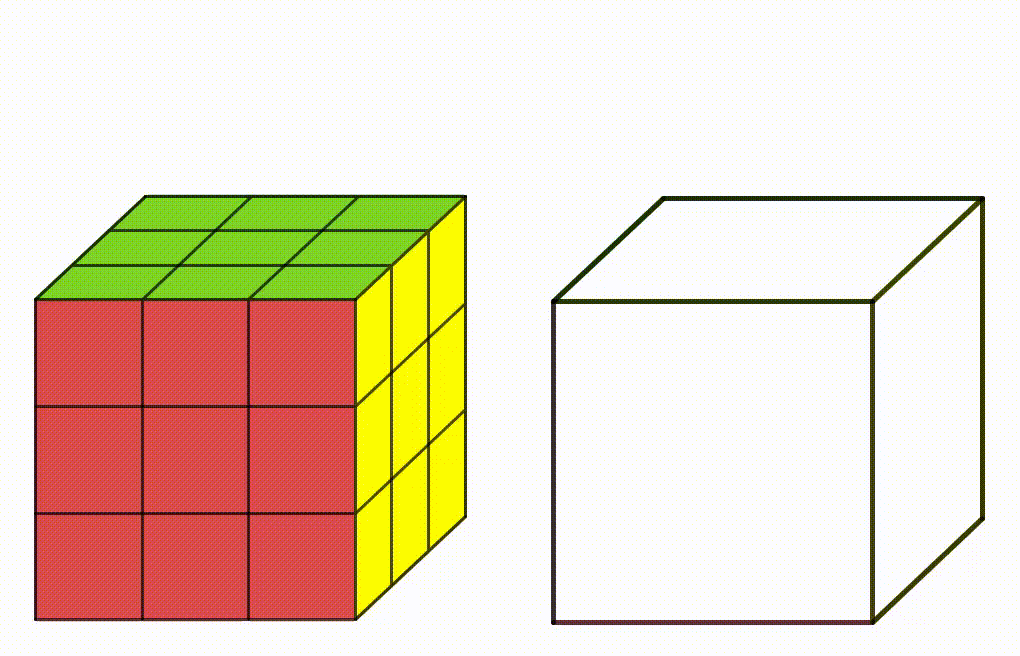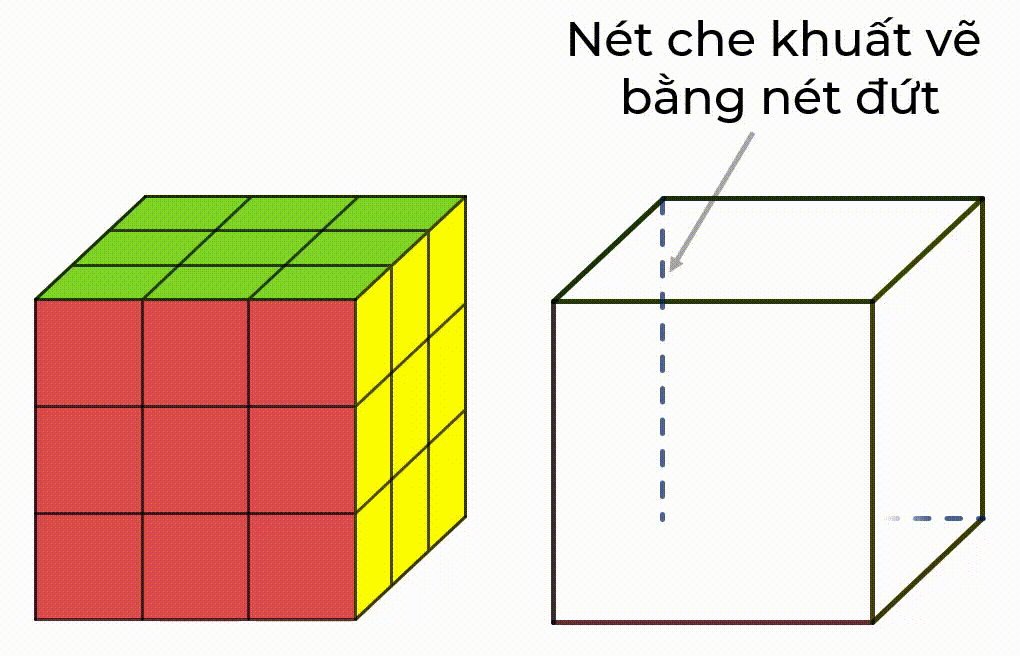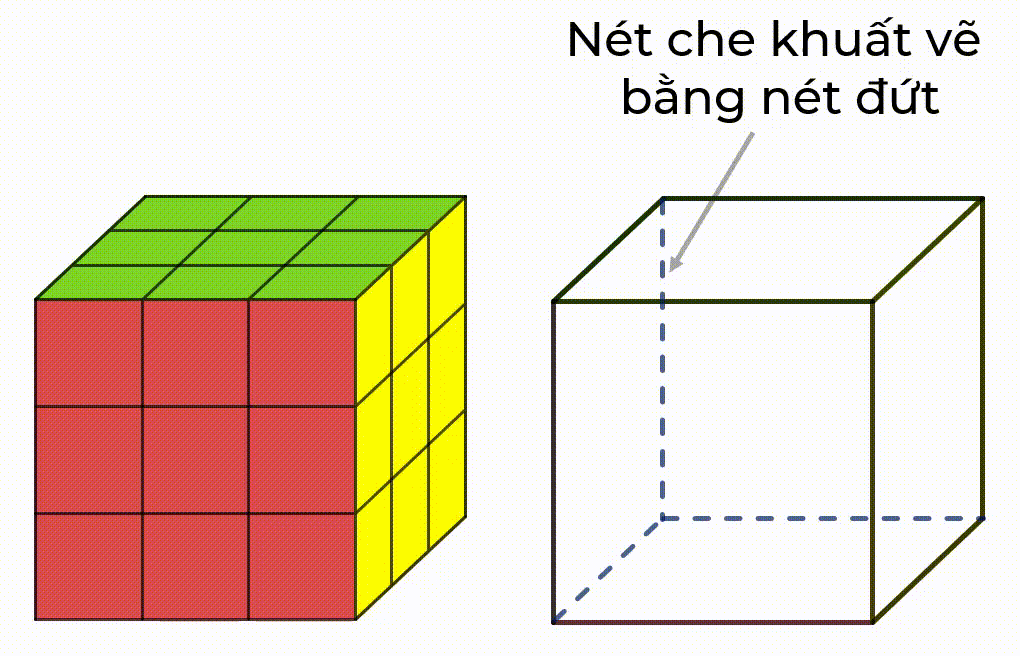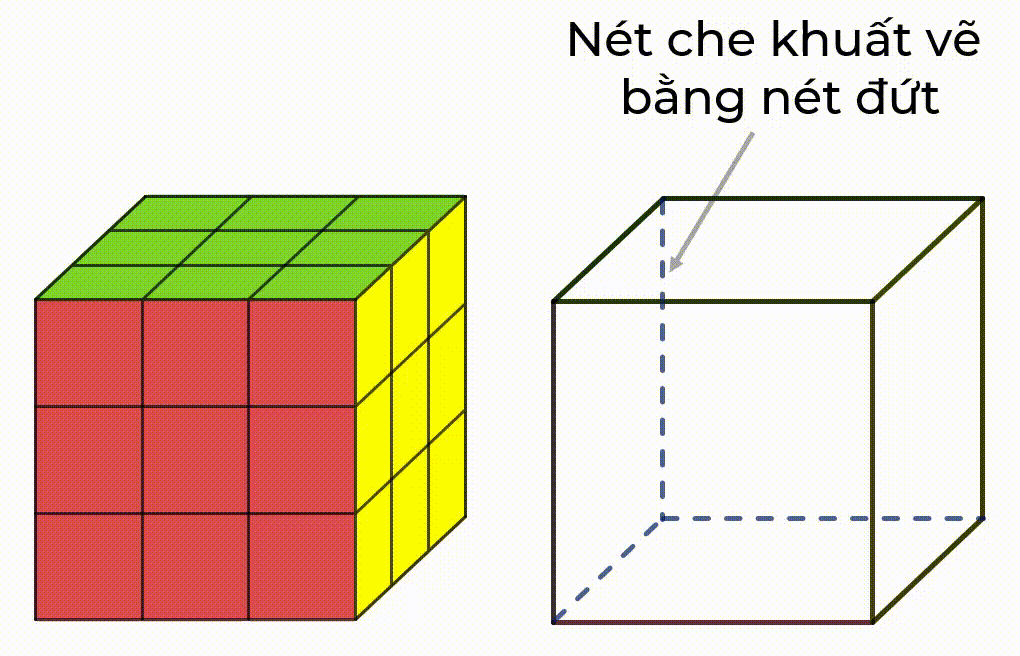
- Dùng nét liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn biểu diễn cho đường bị che khuất.

Ví dụ: Ta bổ sung các nét che khuất (nét đứt) khi biểu diễn hình lập phương bằng cách tuân thủ quy tắc:

- Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song.

II. Các tính chất thừa nhận trong không gian.

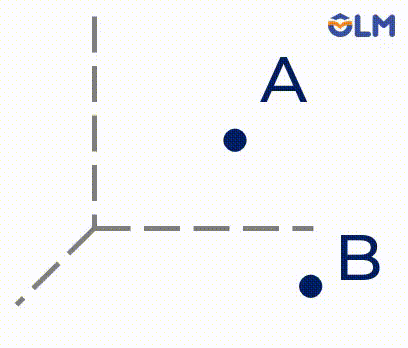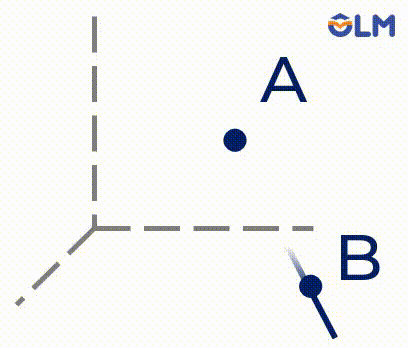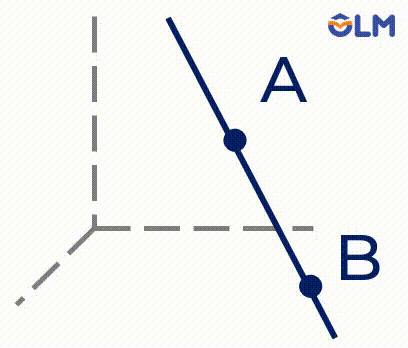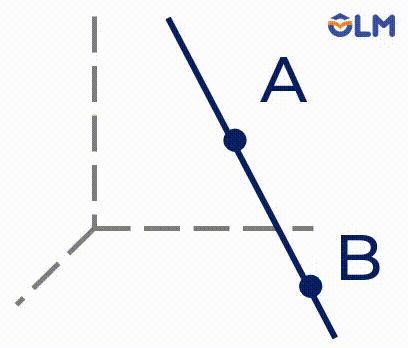
1. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.

2. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.

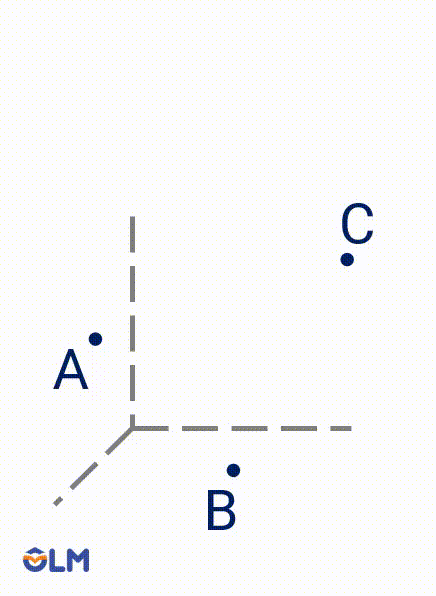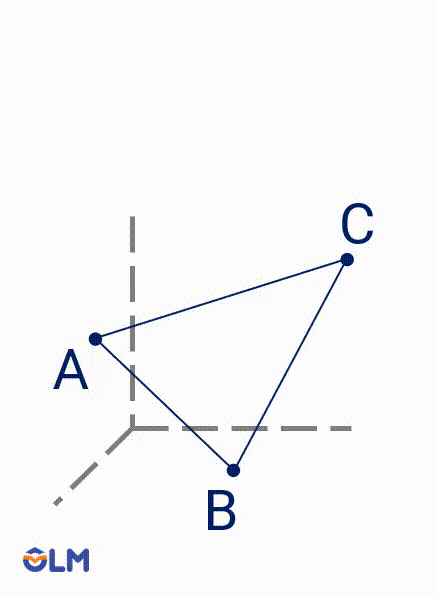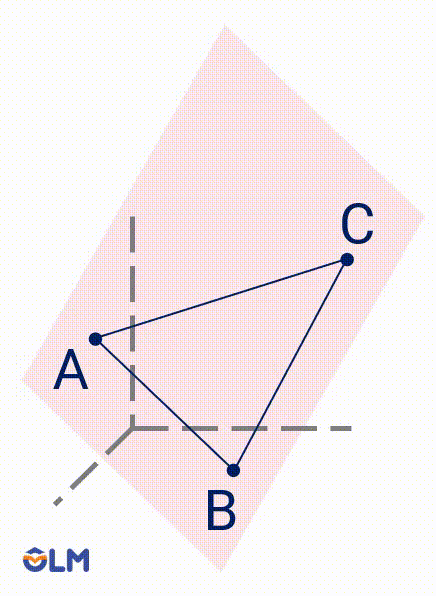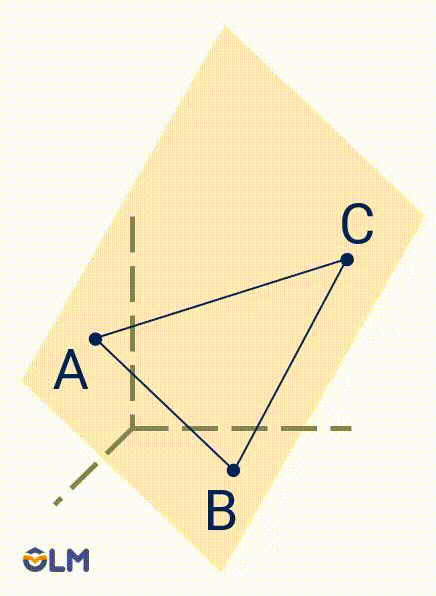
Mặt phẳng trong hình vẽ có thể được kí hiệu bởi tên của ba điểm, mặt phẳng $(ABC)$.

3. Tồn tại bốn điểm không cùng một mặt phẳng (không đồng phẳng).

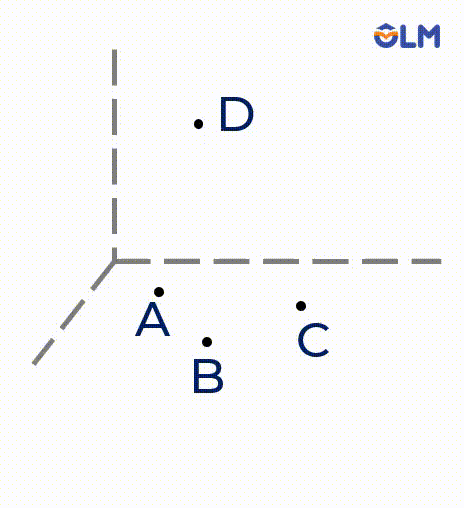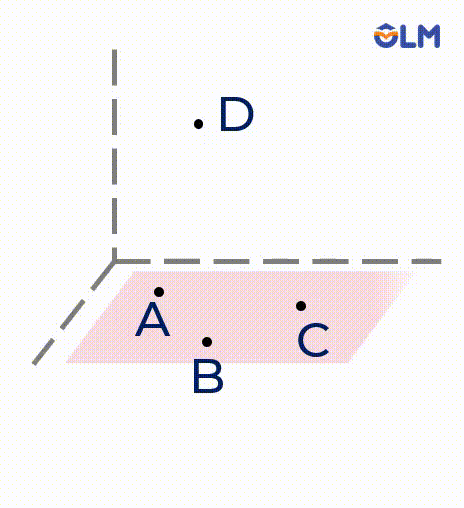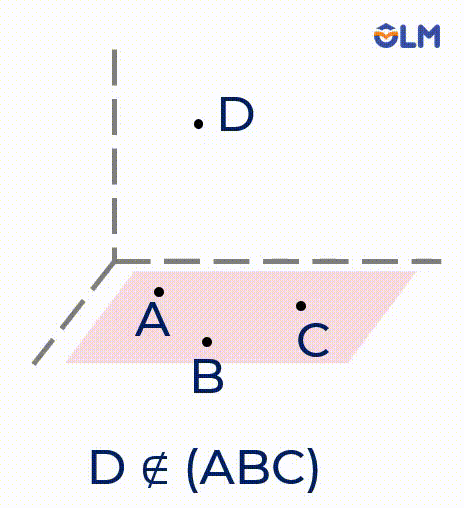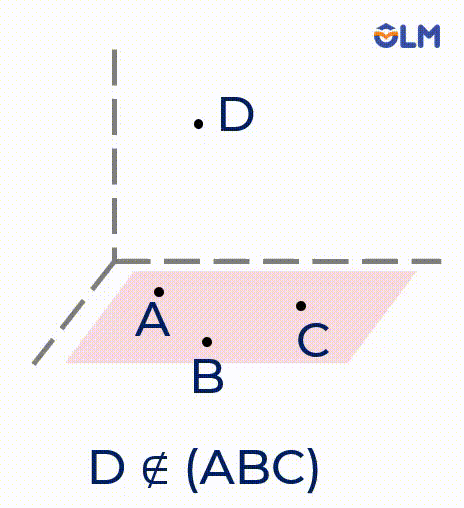
4. Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó.

Chú ý: Nếu mọi điểm của đường thẳng $d$ đều thuộc mặt phẳng $(P)$ thì ta nói đường thẳng $d$ nằm trong $(P)$ hoặc $(P)$ chứa $d$.

Kí hiệu: $d \subset (P)$ hoặc $(P) \supset d$.​

5. Nếu hai mặt phẳng phân biệt có điểm chung thì có vô số điểm chung, tập hợp các điểm chung này là một đường thẳng.

Chú ý: Đường thẳng $d$ chung của hai mặt phẳng $(P)$ và $(Q)$ được gọi là giao tuyến của $(P)$ và $(Q)$. Kí hiệu: $d=(P) \cap (Q)$.

6. Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hình học phẳng đều đúng.​