Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Cách xác định một mặt phẳng, hình chóp và hình tứ diện SVIP
III. Cách xác định một mặt phẳng:
Một mặt phẳng được xác định khi
🔸 biết nó đi qua ba điểm không thẳng hàng.

🔸 biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.

🔸 biết nó chứa hai đường thẳng cắt nhau.
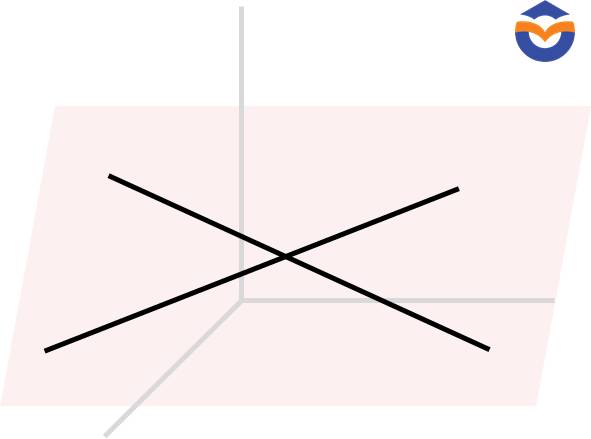
Chú ý. Mặt phẳng được xác định bởi điểm A và đường thẳng d không chứa A được kí hiệu là mp(A,d). Mặt phẳng được xác định bởi hai đường thẳng cắt nhau a và b được kí hiệu mp(a,b).
IV. Hình chóp và hình tứ diện
a) Hình chóp
🔸 Cho đa giác lồi $A_1 A_2 ... A_n$ và một điểm $S$ nằm ngoài mặt phẳng chứa đa giác đó.
Nối $S$ với các đỉnh $A_1; A_2; ... ;A_n$ ta được hình chóp $S. A_1 A_2 ... A_n$.
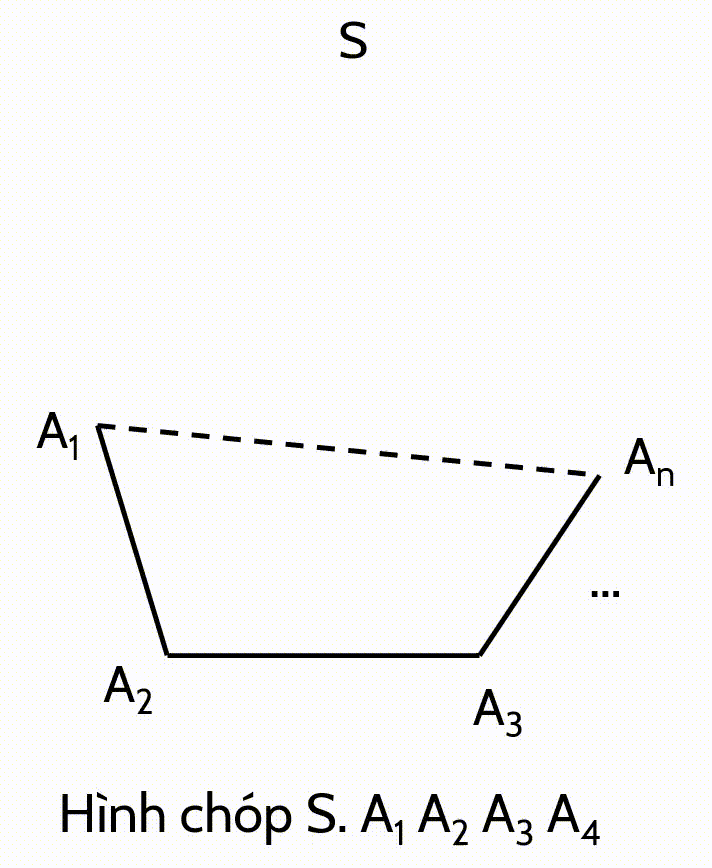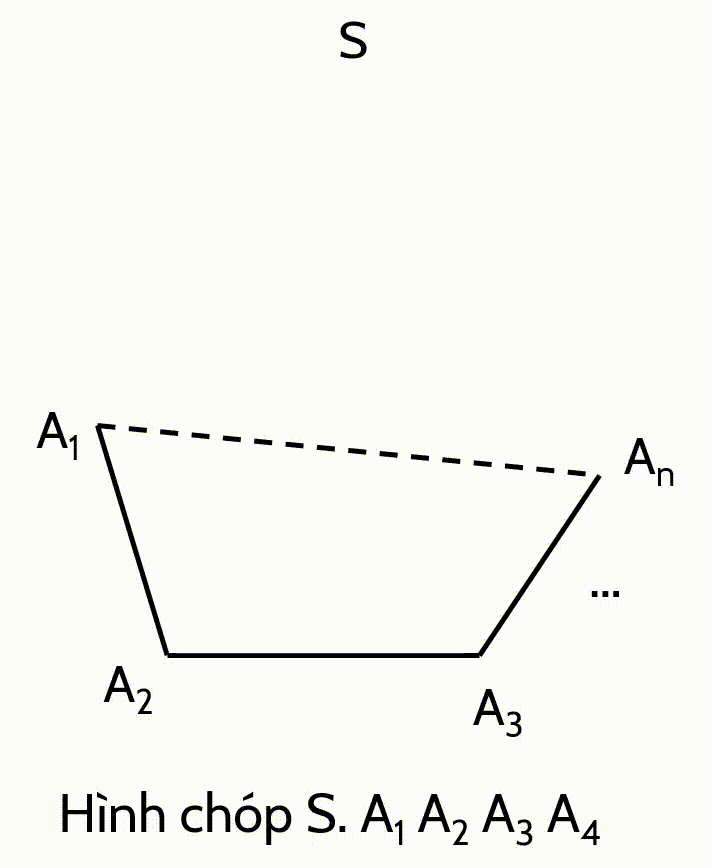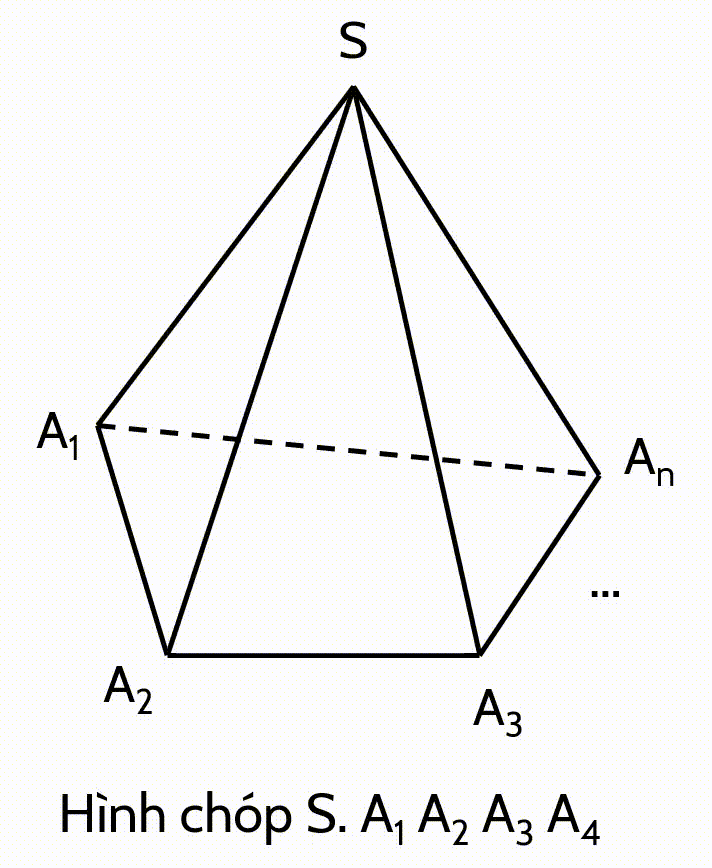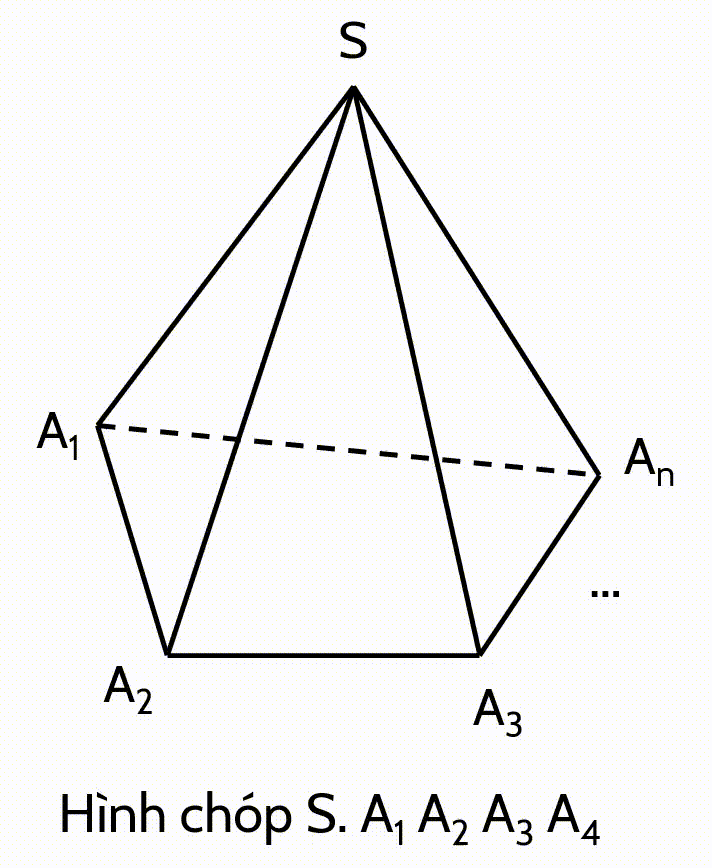
🔸 Hình chóp $S. A_1 A_2 ... A_n$ có điểm $S$ là đỉnh và đa giác $A_1 A_2 ... A_n$ là mặt đáy; các tam giác $S A_1 A_2,$ $S A_2 A_3,...$ và $S A_n A_1,$ là các mặt bên; các cạnh $S A_1,$ $S A_2 ,...$ và $S A_n$ là các cạnh bên; cách cạnh $A_1 A_2,\, A_2 A_3,\, ... A_n A_1$ được gọi là các cạnh đáy.
b) Hình tứ diện
🔸 Định nghĩa: Hình tứ diện là hình chóp có đáy là một tam giác, hay là hình được xác định bởi $4$ điểm không đồng phẳng.

🔸 Trong hình tứ diện $A B C D$, các điểm $A, B, C, D$ được gọi là các đỉnh của tứ diện, các đoạn thẳng $A B, B C$, $C D, D A, A C, B D$ được gọi là các cạnh của tứ diện, các tam giác $A B C, A C D, A B D, B C D$ được gọi là các mặt của tứ diện.
🔸 Trong hình tứ diện, hai cạnh không có đỉnh chung được gọi là hai cạnh đối diện, đỉnh không nằm trên một mặt được gọi là đỉnh đối diện với mặt đó.
Nhận xét. Hình tứ diện là một hình chóp tam giác mà mặt nào của hình tứ diện cũng có thể được coi là mặt đáy.

Bạn có thể đánh giá bài học này ở đây