Ba đường conic trong mặt phẳng tọa độ SVIP

1. ELIP

Nhận biết elip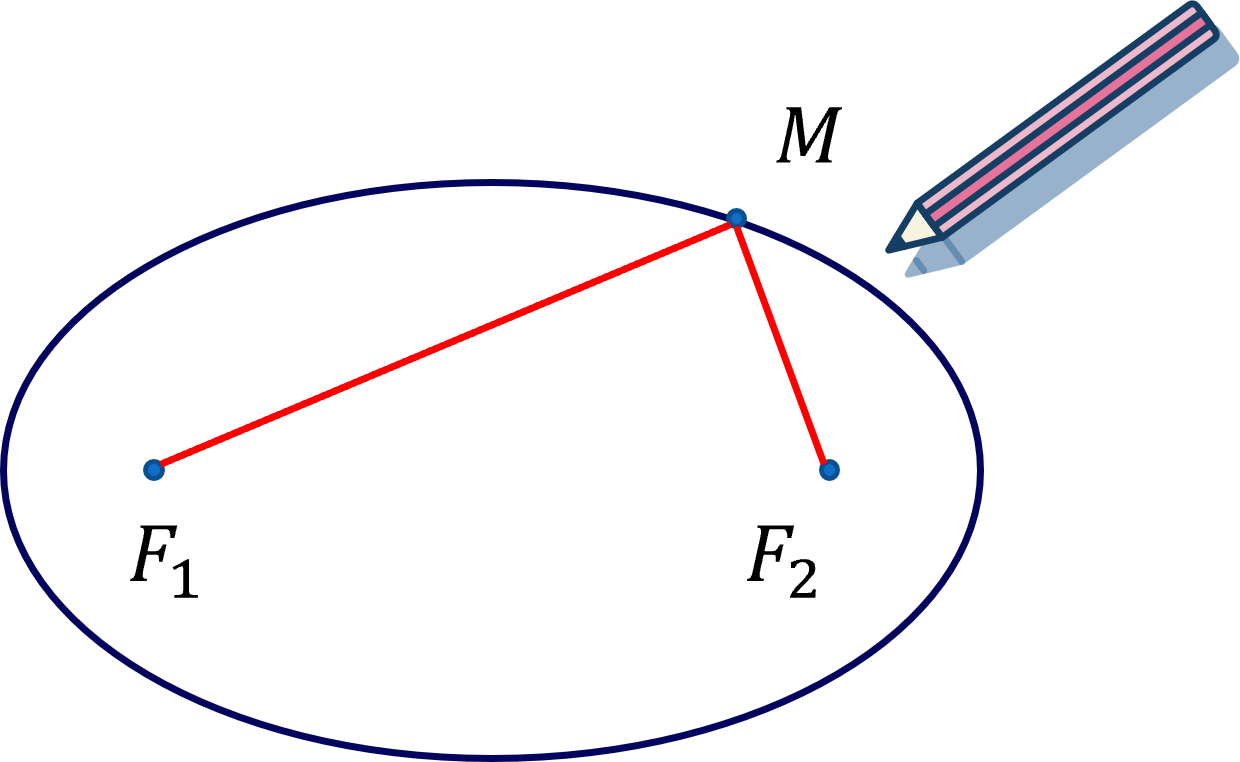

Cho hai điểm cố định \(F_1\), \(F_2\) và một độ dài không đổi \(2a\) lớn hơn \(F_1F_2\). Elip \(\left(E\right)\) là tập hợp các điểm \(M\) trong mặt phẳng sao cho \(F_1M+F_2M=2a\).

Các điểm \(F_1\) và \(F_2\) gọi là các tiêu điểm của elip. 

Độ dài \(F_1F_2=2c\) gọi là tiêu cự của elip (\(a>c\)).

Phương trình chính tắc của elip

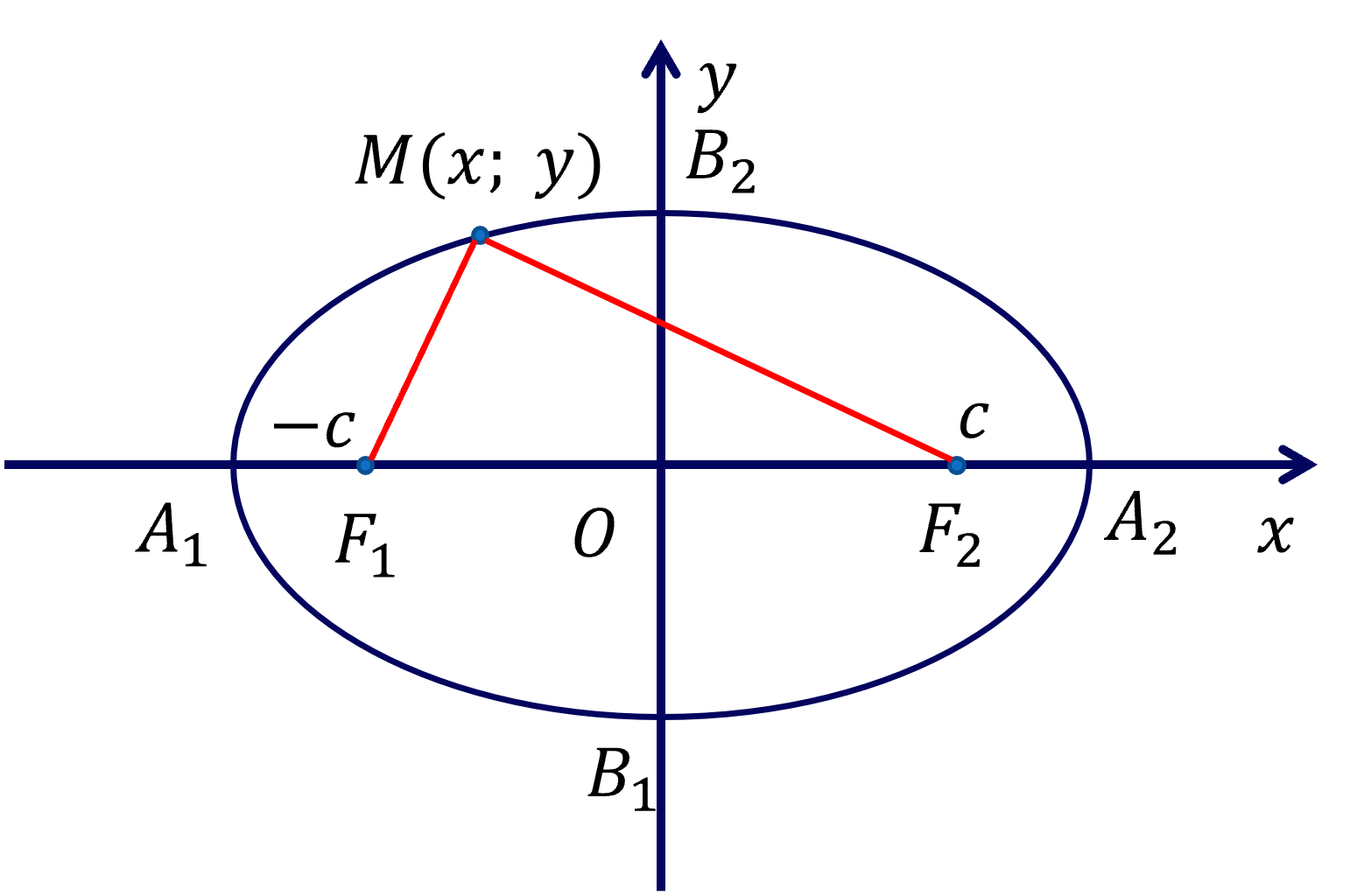
Cho elip \(\left(E\right)\) có hai tiêu điểm là \(F_1\), \(F_2\).

Chọn hệ trục tọa độ \(Oxy\) sao cho \(F_1\left(-c;0\right)\) và \(F_2\left(c;0\right)\).

Phương trình \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), trong đó \(b=\sqrt{a^2-c^2}\) gọi là phương trình chính tắc của elip. 

Chú ý:

• \(\left(E\right)\) cắt \(Ox\) tại hai điểm \(A_1\left(-a;0\right)\), \(A_2\left(a;0\right)\) và cắt \(Oy\) tại hai điểm \(B_1\left(0;-b\right)\), \(B_2\left(0;b\right)\). 
• Các điểm \(A_1\), \(A_2\), \(B_1\), \(B_2\) gọi là các đỉnh của elip. 
• Đoạn thẳng \(A_1A_2\) gọi là trục lớn, đoạn thẳng \(B_1B_2\) gọi là trục nhỏ của elip.
• Giao điểm \(O\) của hai trục là tâm đối xứng của elip. 
• Nếu \(M\left(x;y\right)\in\left(E\right)\) thì \(\left|x\right|\le a\), \(\left|y\right|\le b\).

Ví dụ: Cho elip \(\left(E\right):\dfrac{x^2}{169}+\dfrac{y^2}{25}=1\). 

a) Tìm tọa độ hai tiêu điểm, tiêu cự của \(\left(E\right)\).

b) Cho điểm \(M\) bất kì thuộc \(\left(E\right)\). Tính \(MF_1+MF_2\).

c) Cho điểm \(M\) thuộc \(\left(E\right)\) sao cho \(M\) nhìn hai tiêu điểm dưới một góc vuông. Tính đoạn \(OM\), trong đó \(O\) là gốc tọa độ, từ đó hãy tìm tọa độ điểm \(M\).

Giải

a) Trong phương trình chính tắc của \(\left(E\right)\) ta có

\(a^2=169,b^2=25\Rightarrow a=13,b=5,c=\sqrt{a^2-b^2}=\sqrt{169-25}=12\).

Vậy \(\left(E\right)\) có hai tiêu điểm là \(F_1\left(-c;0\right)=\left(-12;0\right)\), \(F_2\left(c;0\right)=\left(12;0\right)\), có tiêu cự là \(2c=2.12=24\). 

b) Vì điểm \(M\) thuộc \(\left(E\right)\) nên \(MF_1+MF_2=2a=2.13=26\).

c) Gọi \(M\left(x_0;y_0\right)\). Do \(M\) thuộc \(\left(E\right)\) nên ta có \(\dfrac{x_0^2}{169}+\dfrac{y_0^2}{25}=1\) (1).

Theo giả thiết ta có \(\widehat{F_1MF_2}=90^o\), mà \(O\) là trung điểm của \(F_1F_2\) nên ta có \(OM=\dfrac{F_1F_2}{2}=c=12\).

Suy ra \(x_0^2+y_0^2=12^2=144\Leftrightarrow y_0^2=144-x_0^2\). (2) 

Từ (1) và (2) ta suy ra

 \(\dfrac{x_0^2}{169}+\dfrac{144-x_0^2}{25}=1\Leftrightarrow x_0^2=\dfrac{20111}{144}\Leftrightarrow x_0=\pm\dfrac{13\sqrt{119}}{12}\).

Thay \(x_0\) vào (2) ta được 

 \(y_0^2=144-x_0^2=144-\dfrac{20111}{144}=\dfrac{625}{144}\Leftrightarrow y_0=\pm\dfrac{25}{12}\).

Vậy \(OM=12\) và có bốn điểm \(M\) thỏa mãn đề bài, các điểm này có tọa độ là

\(M_1\left(\dfrac{13\sqrt{119}}{12};\dfrac{25}{12}\right),M_2\left(\dfrac{13\sqrt{119}}{12};-\dfrac{25}{12}\right),M_3\left(-\dfrac{13\sqrt{119}}{12};\dfrac{25}{12}\right),M_4\left(-\dfrac{13\sqrt{119}}{12};-\dfrac{25}{12}\right)\).

Cách khác: Để tìm tọa độ điểm \(M\), ta có thể giải hệ \(\left\{{}\begin{matrix}M\in\left(E\right)\\\overrightarrow{MF_1}.\overrightarrow{MF_2}=0.\end{matrix}\right.\)

2. HYPEBOL

Nhận biết hypebol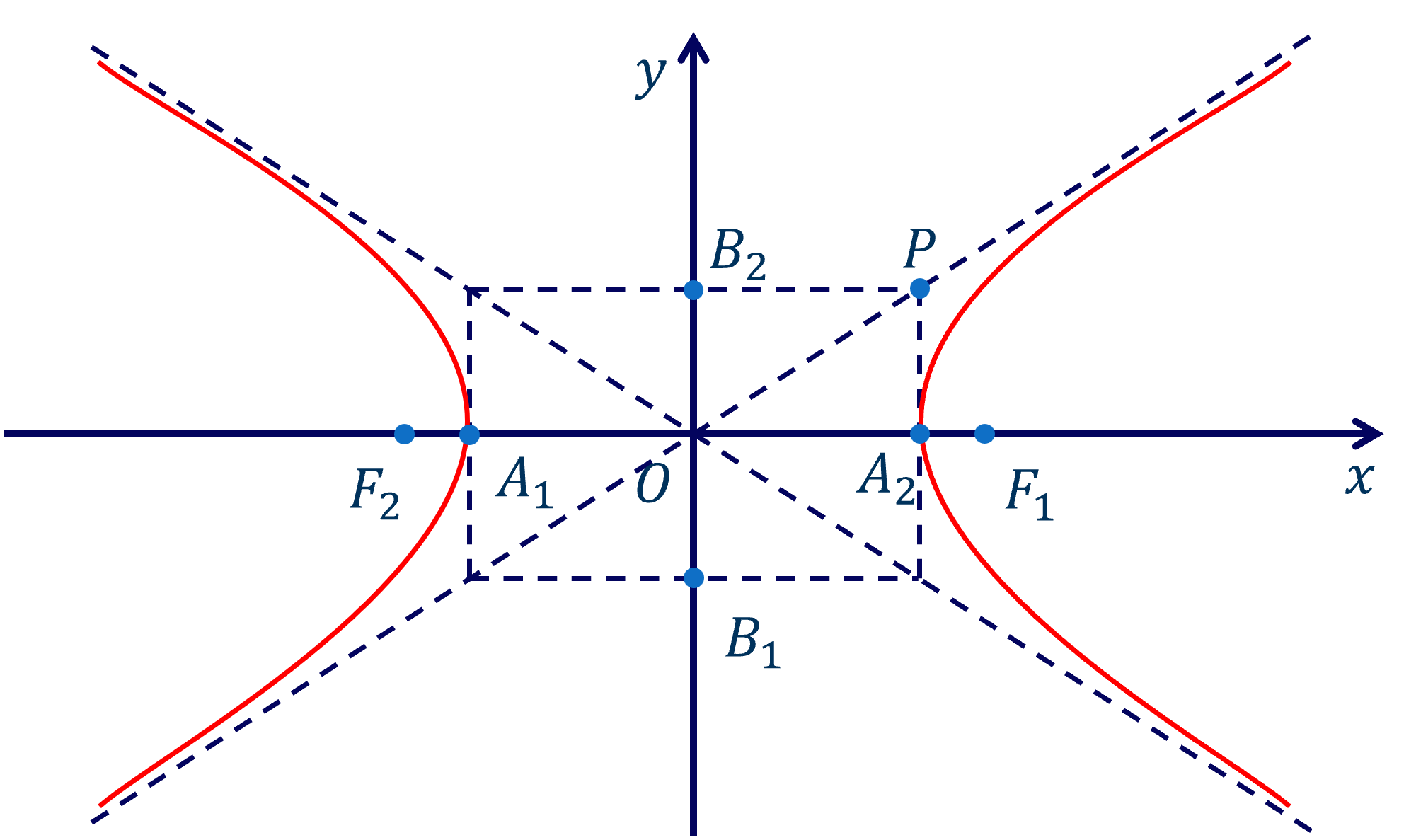

Cho hai điểm cố định \(F_1\), \(F_2\) và một độ dài không đổi \(2a\) nhỏ hơn \(F_1F_2\). Hypebol là tập hợp các điểm \(M\) trong mặt phẳng sao cho \(\left|F_1M-F_2M\right|=2a\).

Các điểm \(F_1\), \(F_2\) gọi là các tiêu điểm của hypebol.

Độ dài \(F_1F_2=2c\) gọi là tiêu cự của hypebol (\(c>a\)). 

Phương trình chính tắc của hypebol

Hypebol \(\left(H\right)\) có hai tiêu điểm là \(F_1\), \(F_2\). Chọn hệ trục tọa độ sao cho \(F_1\left(-c;0\right)\) và \(F_2\left(c;0\right)\). Phương trình \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\) trong đó \(b=\sqrt{c^2-a^2}\) là phương trình chính tắc của hypebol. 

Chú ý:

• \(\left(H\right)\) cắt \(Ox\) tại hai điểm \(A_1\left(-a;0\right)\) và \(A_2\left(a;0\right)\). Nếu vẽ hai điểm \(B_1\left(0;-b\right)\) và \(B_2\left(0;b\right)\) vào hình chữ nhật \(OA_2PB_2\) \(\sqrt{a^2+b^2}=c\).
• Các điểm \(A_1\), \(A_2\) gọi là các đỉnh của hypebol.
• Đoạn thẳng \(A_1A_2\) gọi là trục thực, đoạn thẳng \(B_1B_2\) gọi là trục ảo của hypebol.
• Giao điểm \(O\) của hai trục gọi là tâm đối xứng của hypebol.
• Nếu \(M\left(x;y\right)\in\left(H\right)\) thì \(x\le-a\) hoặc \(x\ge a\).

Ví dụ: Lập phương trình chính tắc của hypebol \(\left(H\right)\), biết rằng \(\left(H\right)\) có một tiêu điểm là \(F_1\left(-13;0\right)\) và đi qua điểm \(A\left(-5;0\right)\). Tìm điểm \(M\) thuộc \(\left(H\right)\) có hoành độ dương sao cho khoảng cách từ \(M\) đến gốc tọa độ là nhỏ nhất. 

Giải

Phương trình chính tắc của \(\left(H\right)\) có dạng \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\), trong đó \(a,b>0\).

Vì \(\left(H\right)\) đi qua điểm \(A\left(-5;0\right)\) nên \(\dfrac{\left(-5\right)^2}{a^2}-\dfrac{0^2}{b^2}=1\Rightarrow a=5\).

Do \(\left(H\right)\) có một tiêu điểm là \(F_1\left(-13;0\right)\) nên ta có \(c=13\) suy ra \(b^2=c^2-a^2=13^2-5^2=144\).

Vậy phương trình chính tắc của \(\left(H\right)\) là \(\dfrac{x^2}{25}-\dfrac{y^2}{144}=1\).

 Gọi \(M\left(x_0;y_0\right)\) với \(x_0>0\). 

Do \(M\in\left(H\right)\) nên ta có

\(\dfrac{x_0^2}{25}-\dfrac{y_0^2}{144}=1\Leftrightarrow x^2_0=25+\dfrac{25y_0^2}{144}\ge25\).

Suy ra \(x_0\ge5\). 

Từ đó suy ra \(OM=\sqrt{x_0^2+y_0^2}\ge\sqrt{x_0^2}=x_0\ge5\).

Dấu "\(=\)" xảy ra khi và chỉ khi \(\left\{{}\begin{matrix}y_0=0\\x_0=5\end{matrix}\right.\) do đó ta có \(M\left(5;0\right)\).

3. PARABOL

Nhận biết parabol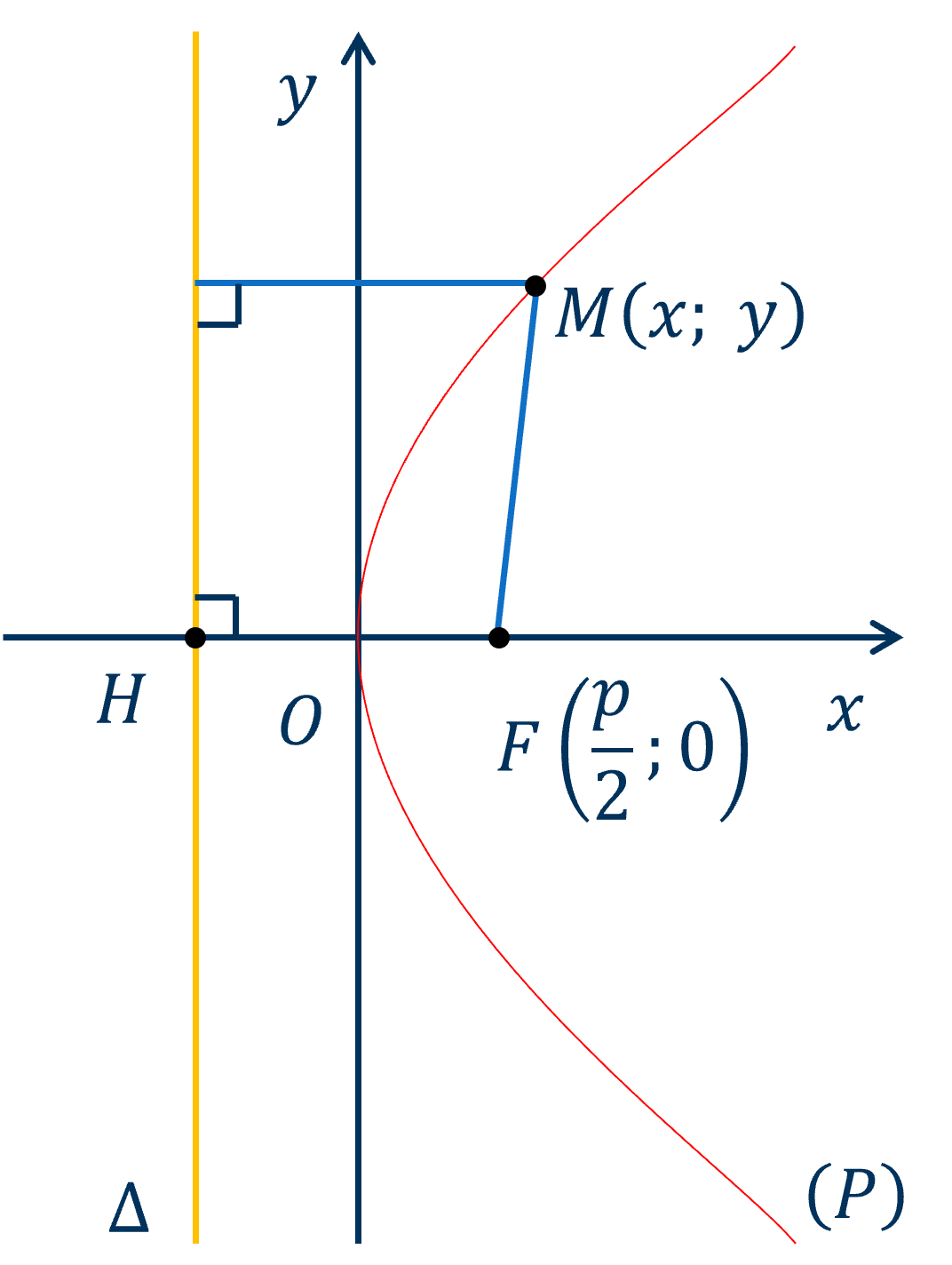

Cho một điểm cố định \(F\) mà một đường thẳng \(\Delta\) cố định không đi qua \(F\). Parabol \(\left(P\right)\) là tập hợp các điểm \(M\) cách đều \(F\) và \(\Delta\).

\(F\) gọi là tiêu điểm và \(\Delta\) gọi là đường chuẩn của parabol \(\left(P\right)\).

Phương trình chính tắc của parabol 

Parabol \(\left(P\right)\) với tiêu điểm \(F\left(\dfrac{p}{2};0\right)\) và đường chuẩn \(\Delta:x+\dfrac{p}{2}=0\), có phương trình chính tắc: \(y^2=2px\).

Chú ý: 

• \(O\) gọi là đỉnh của parabol \(\left(P\right)\).
• \(Ox\) gọi là trục đối xứng của parabol \(\left(P\right)\).
• \(p\) gọi là tham số tiêu của parabol \(\left(P\right)\).
• Nếu \(M\left(x;y\right)\in\left(P\right)\) thì \(x\ge0\) và \(M'\left(x;-y\right)\in\left(P\right)\).  

Ví dụ: Cho parabol \(\left(P\right)\) có phương trình ở dạng chính tắc và \(\left(P\right)\) đi qua điểm \(A\left(3;6\right)\). 

a) Viết phương trình của \(\left(P\right)\).

b) Tìm tọa độ tiêu điểm \(F\), phương trình đường chuẩn \(\Delta\) và tham số tiêu \(p\) của \(\left(P\right)\). 

c) Cho điểm \(M\) thuộc \(\left(P\right)\) và có hoành độ bằng \(4\). Tính độ dài đoạn thẳng \(MF\).

Giải

a) Phương trình chính tắc của \(\left(P\right)\) có dạng \(y^2=2px\), trong đó \(p>0\).

Vì \(A\left(3;6\right)\) thuộc \(\left(P\right)\) nên ta có phương trình

\(6^2=2.p.3\Leftrightarrow p=6\).

Vậy phương trình chính tắc của \(\left(P\right)\) là \(y^2=12x\). 

b) \(\left(P\right)\) có tiêu điểm là \(F\left(\dfrac{p}{2};0\right)=\left(3;0\right)\), phương trình đường chuẩn \(\Delta\) là \(x+\dfrac{p}{2}=0\Leftrightarrow x+3=0\) và có tham số tiêu là \(p=6\).

c) Vì điểm \(M\) thuộc \(\left(P\right)\) nên ta có 

\(MF=d\left(M,\Delta\right)=\dfrac{\left|4+3\right|}{\sqrt{1^2+0^2}}=7\).