Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Hypebol SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Cho hai điểm \(F_1,F_2\) cố định có khoảng cách \(F_1F_2=2c\left(c>0\right)\).
Đường hypebol (hay hypebol) là tập hợp các điểm \(M\) sao cho \(\left|MF_1-MF_2\right|=2a\), \(c>a>0\).
Hai điểm \(F_1\) và \(F_2\) được gọi là tiêu điểm của hypebol.
Khi chọn hệ trục tọa độ như hình vẽ thì phương trình chính tắc của đường hypebol \(\left(H\right)\) là:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1,a>0,b>0\).
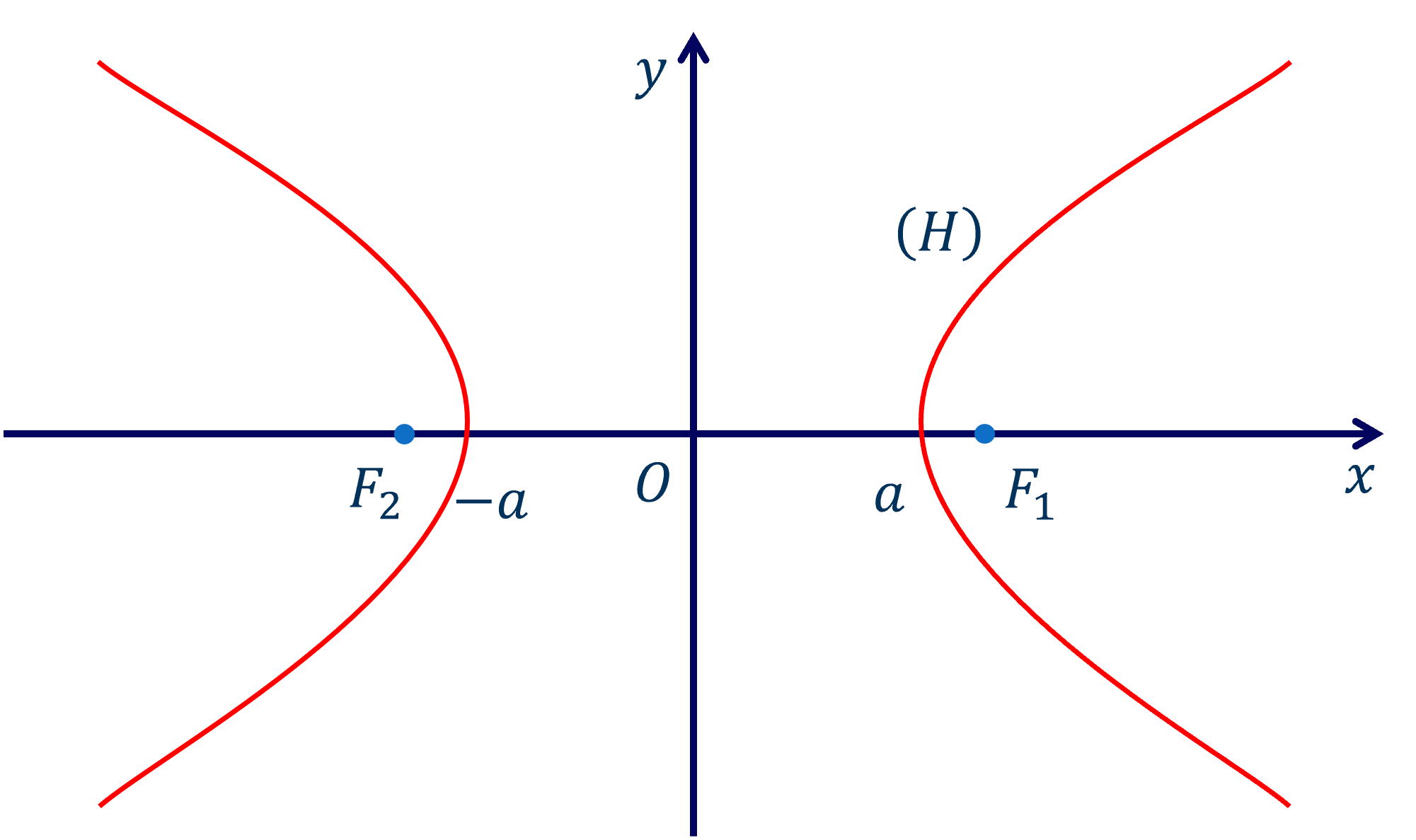
\(F_1\left(-c;0\right),F_2\left(c;0\right)\) là hai tiêu điểm, \(c^2=a^2+b^2\).
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- mở rộng 1 nhưng bạn biết thì trên mặt
- phẳng nếu mà hai thiết bị đặt tại các vị
- trí theo một F2 nhận được một ký hiệu âm
- thanh cùng lúc thì vị trí phát tín hiệu
- cách đều 2 điểm f1 f2 do đó nó nằm trên
- đường trung trực của đoạn thẳng S1 F2
- vậy nếu ta giả sử thiết bị là tại F2
- nhận được tín hiệu âm thanh sớm hơn
- thiết bị thật là F1 2 giây và vận tốc âm
- thanh là 343 m/s
- ta tìm mối quan hệ giữa khoảng cách từ
- nơi phát ra tín hiệu âm thanh tới f1s2
- ý B việc giới hạn khu vực tìm kiếm nơi
- phát ra tín hiệu âm thanh có liên quan
- gì đến bài toán thì tổng hợp những điểm
- M thỏa mãn
- ms2 bằng 6862 không
- E nếu ta nơi phát ra thì âm thanh để mở
- thì sẽ có m F1
- trừ 1f2
- đây là hiệu khoảng cách từ M đến F1 và M
- đến F2
- thiết bị tại F2 nhận được tín hiệu âm
- thanh sớm hơn thiết bị tại F1 là 2 giây
- mà ta có vận tốc âm thanh là 343 m/s
- 343 m/s làm vận tốc
- từ vận tốc khoảng thời gian thì ta thấy
- được quãng đường s sẽ bằng v điểm
- 3 đến 2
- 1986
- do đó mới 1 - mf2 sẽ bằng 686 và đơn vị
- là mét
- B nếu mà ta biết được tập hợp những điểm
- M thỏa mãn ms1 - F2 = 686 m thì ta có
- thể giới hạn khu vực tìm kiếm nó nằm
- trong tổ hợp này
- và ví dụ này cũng cho thấy ý nghĩa của
- bài toán tìm tập hợp những điểm thỏa mãn
- điều kiện cho trước trong thực tế vậy
- tập hợp những điểm này gọi là gì thì ta
- có định nghĩa
- cho hai điểm phân biệt và cố định f1 f2
- đặt E1 F2 = 2C cho sức Dương A nhỏ hơn c
- ta có tập hợp điểm M thỏa mãn giá trị
- tuyệt đối của ms1 -1 F2 = 2A được gọi là
- đường hyperbol hay là hyperbol hai điểm
- f1 f2 được gọi là hai thời điểm và
- khoảng cách f1 f2 khoảng 2C được gọi là
- tiêu cự của chi tiêu đó
- có câu hỏi nhỏ tại sao cho mình những
- Hippo thì ta cần điều kiện A nhỏ hơn C
- ta có trong tam giác m f1 f2
- thì f1 f2
- theo bất đẳng thức tam giác
- f1 f2 Thì đó thì ta có 2a
- ta có chú ý khi phải buồn rây có hai
- nhánh
- Một nhánh gồm những điểm M thỏa mãn mf1
- - 12 = 2a và nhớ còn lại là những điểm M
- thỏa mãn ms1 - mf2 bằng -2a Hoặc là nếu
- ta chuyển biến đổi dấu ta thu được mf2
- trừ nữa 1 bằng 2a
- những điểm M thuộc nhánh gần F1 thì ta
- có làm ms1 - ms2 bằng -2a
- = -2a
- Còn dây M thuộc nhánh gần F2 thì có
- ms2 = 22
- ta sang phần Ví dụ
- 3
- trên biển có hai đảo hình tròn với bán
- kính khác nhau tại vùng biển giữa hai
- đảo đó thì chúng ta xác định được một
- ranh giới cách đều hai đảo tức là khoảng
- cách từ 4 vị trí trên đó đến hai đảo là
- bằng nhau Hỏi đường ranh giới đó có
- thuộc một nhánh của một khi po hay không
- ở đây tại Nghĩa khoảng cách từ một vị
- trí bất kỳ trên biển tới đảo cho nó là
- bằng hiệu của khoảng cách từ vị trí đó
- đến tâm đảo và bán kính của đảo
- là nếu thầy mà lấy một điểm bất kì
- M trên biển
- Vụ gì đây là bán kính thì khoảng cách từ
- điểm M đến đảo là mo trừ đi Oy
- tại các điểm như trên hình đây có một O2
- tâm của các đảo M là một điểm bất kì ở
- trên biển sao cho khoảng cách từ M đến
- hai đảo có tâm o1 và U2 là bằng nhau
- ở đây ta giả sử đẳng nhất của tâm o1 và
- bán kính R1 và thứ hai có tâm O2 và bán
- kính R2
- do hai đường tròn o1 R1 U2 R2 nằm ngoài
- nhau là có 1 O2 lớn hơn R1 + R2
- ta gọi M là điểm bất kì thuộc cạnh giới
- vì điểm m cách đều hay đảo là m o 1 - R1
- = m2 - R2 đây là theo định nghĩa khoảng
- cách từ một sóng biển đến đảo
- 1 - mũ 2 bằng R1 - R2 và cách chỉnh vế
- đổi dấu
- mặt R1 - R2 đây là một số không đổi
- do đó
- mo1-12 là không đổi
- vậy
- F1 trùng với o1 F2 với O2
- tiêu cự 2 c bằng o1 O2
- a bằng giá trị tuyệt đối của R1 -
- r24h với các ký hiệu như trong định
- nghĩa không
- thứ hai lộ c0
- trong hoạt động này chúng ta đã gắn fivv
- vào trong một thị trường có độ
- mờ có độ xy
- ta phải tính f1m và f2m theo x y và c
- b Giải thích vì sao điểm m x y cabon khi
- mặt nước sau được thỏa mãn
- độ dài của vectơ
- F11
- x + c y vector f2m bằng IC y
- độ dài của Vectơ ta tính được f1m khoảng
- độ dài vectơ f1m sẽ bằng x + c² + y²
- f2m
- -
- f2ma tại định được f1m sẽ bằng
- C bình phương
- cộng với y bình phương sau đó ta có
- chứng minh
- trừ căn của x trừ c bình phương cộng x
- bình phương bằng 2a
- bằng cách đặt B = C bình trừ A Bình lấy
- căn thì ta sẽ đưa về là x bình a bình
- trừ y bình cộng b bình bằng 1
- về dạng dưới đây thì là hoàn toàn là
- biến đổi tần số
- ở đây các em có thể tự suy nghĩ ở nhà từ
- dạng này thì ta có định nghĩa của HIV
- bằng 1 với a và b lớn hơn 0
- u là trung điểm đoạn nối là do cách đặt
- Liverpool
- có tốc độ là
- chữ C không
- phải F2 có tốc độ là c0
- có hai thời điểm là F1 trừ căn của a
- bình cộng b bình không F2 căn của a bình
- cộng b bình không tiêu cự là 2C bằng 2
- căn 2 bình cộng b bình và giá trị tuyệt
- đối của hiệu các khoảng cách từ mỗi điểm
- của HIV
- F1 chứ 1 F2 lấy giá trị tuyệt đối
- phương trình chính tắc của hidro tương
- Ở đây các em nhớ chú ý là
- không hơn A và B và nhóm c
- a và nhóm c do tập b bằng căn của C mình
- cho A Bình là b bình sẽ bằng C bình trừ
- a bình tương đương với C bình bằng a
- bình
- sau đó C sẽ lớn hơn cả a và b
- phân số dưới đây là phần a và b lớn
- không đổi ta không có điều kiện gì ràng
- buộc giữa a và b
- sau phần Ví dụ
- có phương trình chính tắc là x bình phần
- 64 xử lý Bình phần 225 bằng 1
- ta cần tìm các địa điểm và tiêu cự của
- những cái môn hiệu có khoảng cách từ một
- điểm nằm trên hitable tới hai thời điểm
- có giá trị tuyệt đối bằng bao nhiêu
- ta có a bình bằng 64 b bình bằng 225 do
- đó C = căn của a bình cộng b bình sẽ
- bằng căn của 64 cộng 225 và ta tính được
- bằng 17
- vậy
- F1
- trừ c0
- và tiêu cự là 2C
- bằng 2 x 17 = 34
- hiệu khoảng cách từ một điểm nằm trên
- HIV tới hai thời điểm
- trong bài toán này ta chỉ cần sử dụng
- phương trình chính tắc và định nghĩa thì
- ta sẽ xác định được tiêu điểm tiêu cự và
- giá trị tuyệt đối của hiệu các khoảng
- cách ở điểm nằm trên
- ví dụ tương tự
- cho hydrol có phương trình chính tắc là
- x bình phương 16 trừ y bình phần 9 bằng
- 1
- ta cần tìm các thời điểm và tiêu cự của
- carbon
- ta cũng sử dụng định nghĩa thôi
- bằng 9
- c bằng căn của a bình cộng b bình bằng
- căn của 16 + 9 bằng căn 25 bằng 5
- do đó có thời điểm là F1 -50 f250
OLMc◯2022

Bạn có thể đánh giá bài học này ở đây