Tích vô hướng của hai vectơ SVIP

1. Góc giữa hai vectơ

Cho hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\) khác vectơ \(\overrightarrow{0}\). Từ một điểm \(A\) nào đó, vẽ các vectơ \(\overrightarrow{AB}=\overrightarrow{u}\) và \(\overrightarrow{AC}=\overrightarrow{v}\). Khi đó, số đo của góc \(BAC\) được gọi là số đo góc giữa hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\) hay đơn giản là góc giữa hai vectơ \(\overrightarrow{u}\), \(\overrightarrow{v}\), kí hiệu là \(\left(\overrightarrow{u},\overrightarrow{v}\right)\).

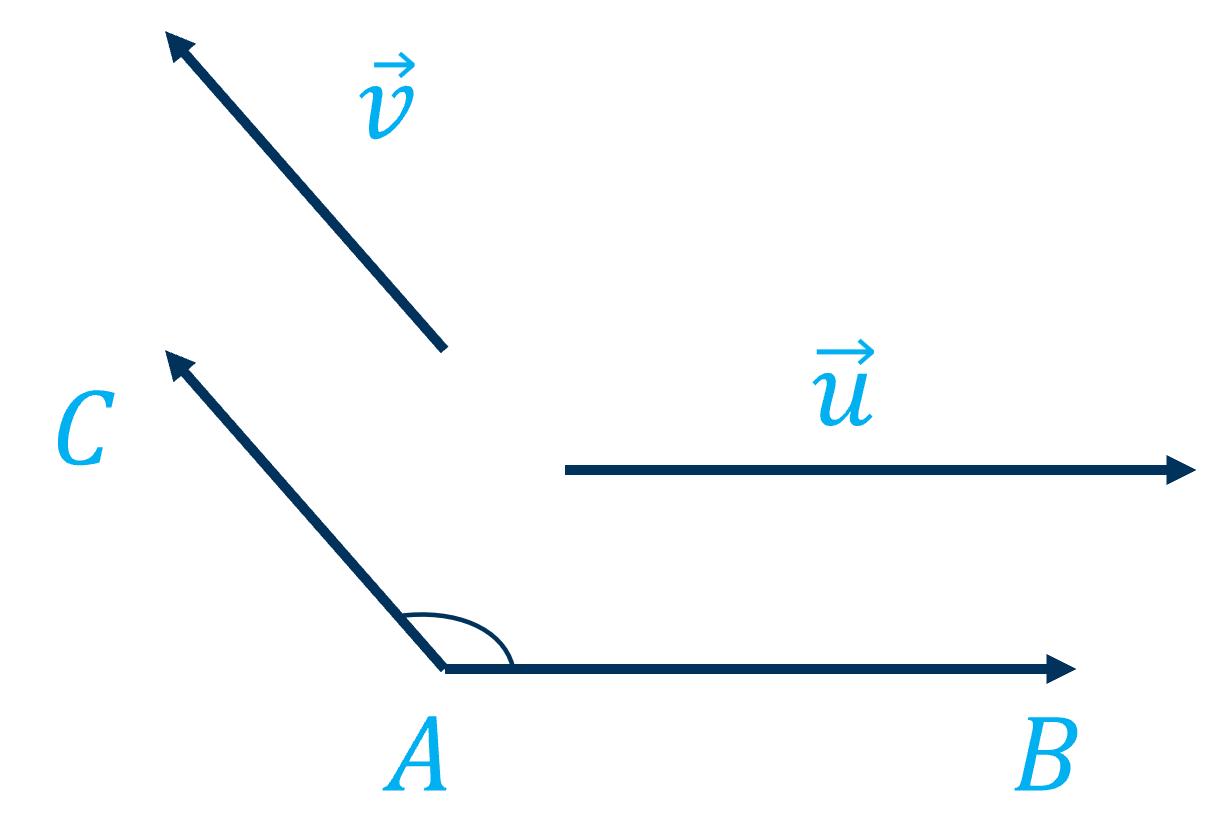
Chú ý

• Quy ước rằng góc giữa hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{0}\) có thể nhận một giá trị tùy ý từ \(0^o\) đến \(180^o\). 
• Nếu \(\left(\overrightarrow{u},\overrightarrow{v}\right)=90^o\) thì ta nói rằng \(\overrightarrow{u}\) và \(\overrightarrow{v}\) vuông góc với nhau, kí hiệu là \(\overrightarrow{u}\perp\overrightarrow{v}\) hoặc \(\overrightarrow{v}\perp\overrightarrow{u}\). Đặc biệt, \(\overrightarrow{0}\) được coi là vuông góc với mọi vectơ.

Ví dụ 1: Cho tam giác \(ABC\) đều tâm \(O\).

Xác định góc giữa các cặp vectơ \(\overrightarrow{AC}\) và \(\overrightarrow{CB}\), \(\overrightarrow{AB}\) và \(\overrightarrow{CB}\), \(\overrightarrow{OA}\) và \(\overrightarrow{BC}\), \(\overrightarrow{OC}\) và \(\overrightarrow{BC}\), \(\overrightarrow{OA}\) và \(\overrightarrow{BO}\).

Giải

Do tam giác \(ABC\) đều nên \(\widehat{ABC}=\widehat{BCA}=\widehat{CAB}=60^o\). 

Dựng hình bình hành \(ADBC\). Khi đó do \(AC=BC\) nên hình bình hành \(ADBC\) là một hình thoi, do đó \(\overrightarrow{AD}=\overrightarrow{CB}\) và \(\widehat{CAD}=180^o-\widehat{BCA}=180^o-60^o=120^o\).

Suy ra \(\left(\overrightarrow{AC},\overrightarrow{CB}\right)=\left(\overrightarrow{AC},\overrightarrow{AD}\right)=\widehat{CAD}=120^o\). 

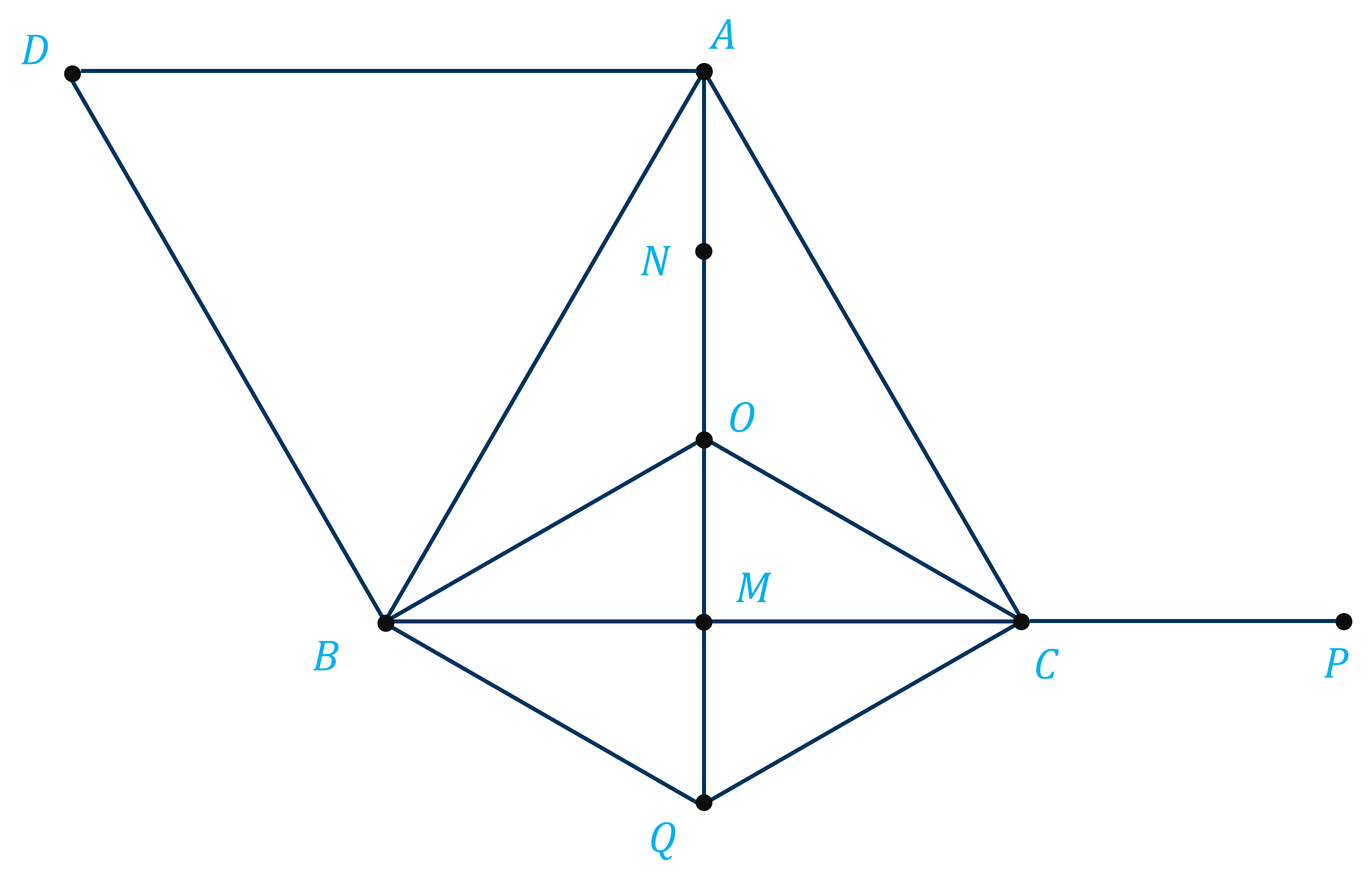
Do \(AD//CB\) suy ra \(\widehat{DAB}=\widehat{ABC}=60^o\) (hai góc so le trong).

Suy ra \(\left(\overrightarrow{AB},\overrightarrow{CB}\right)=\left(\overrightarrow{AB},\overrightarrow{AD}\right)=\widehat{DAB}=60^o\).

Gọi \(M\) là trung điểm của \(BC\) và \(N\) là trung điểm của \(OA\), \(P\) là điểm đối xứng với \(M\) qua \(C\). Khi đó, do \(O\) là tâm của tam giác đều \(ABC\), nên \(A\), \(N\), \(O\), \(M\) thẳng hàng, \(AM\perp BC\), \(\overrightarrow{MN}=\overrightarrow{OA}\) và \(\overrightarrow{MP}=\overrightarrow{BC}\).

Suy ra \(\left(\overrightarrow{OA},\overrightarrow{BC}\right)=\left(\overrightarrow{MN},\overrightarrow{MP}\right)=\widehat{NMP}=90^o\).

Lấy điểm \(Q\) đối xứng với \(O\) qua \(M\). Khi đó tứ giác \(BOCQ\) là một hình thoi, có \(\widehat{CBQ}=\widehat{BCO}=30^o\). 

Suy ra \(\left(\overrightarrow{OC},\overrightarrow{BC}\right)=\left(\overrightarrow{BQ},\overrightarrow{BC}\right)=\widehat{CBQ}=30^o\).

Do \(O\) là trọng tâm của tam giác đều \(ABC\) nên \(OA=\dfrac{2}{3}AM\) suy ra \(OA=OQ\) do đó tam giác \(OQC\) là tam giác đều. 

Suy ra \(\left(\overrightarrow{OA},\overrightarrow{BO}\right)=\left(\overrightarrow{QO},\overrightarrow{QC}\right)=\widehat{OQC}=60^o\).

2. Tích vô hướng của hai vectơ

Tích vô hướng của hai vectơ khác vectơ-không \(\overrightarrow{u}\) và \(\overrightarrow{v}\) là một số, kí hiệu \(\overrightarrow{u}.\overrightarrow{v}\), được xác định bởi công thức \(\overrightarrow{u}.\overrightarrow{v}=\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|.\cos\left(\overrightarrow{u},\overrightarrow{v}\right)\).

Chú ý

•  \(\overrightarrow{u}\perp\overrightarrow{v}\Leftrightarrow\overrightarrow{u}.\overrightarrow{v}=0\).
• \(\overrightarrow{u}.\overrightarrow{u}\) còn được viết là \(\overrightarrow{u}^2\) và được gọi là bình phương vô hướng của vectơ \(\overrightarrow{u}\).

Ta có \(\overrightarrow{u}^2=\left|\overrightarrow{u}\right|.\left|\overrightarrow{u}\right|.\cos0^o=\left|\overrightarrow{u}\right|^2\).

Ví dụ 2: Cho tam giác đều \(ABC\) tâm \(O\), có độ dài các cạnh bằng \(1\). 

Tính tích vô hướng của các cặp vectơ sau  \(\overrightarrow{AC}\) và \(\overrightarrow{CB}\), \(\overrightarrow{AB}\) và \(\overrightarrow{CB}\), \(\overrightarrow{OA}\) và \(\overrightarrow{BC}\), \(\overrightarrow{OC}\) và \(\overrightarrow{BC}\), \(\overrightarrow{OA}\) và \(\overrightarrow{BO}\).

Giải

Do \(AM\perp BC\) nên \(AM=\sqrt{AB^2-BM^2}=\sqrt{1^2-\left(\dfrac{1}{2}\right)^2}=\dfrac{\sqrt{3}}{2}\).

Do \(O\) là tâm của tam giác đều \(ABC\) nên \(\left|\overrightarrow{OB}\right|=\left|\overrightarrow{OA}\right|=OA=\dfrac{2}{3}AM=\dfrac{2}{3}.\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}}{3}\).

Làm tương tự ví dụ 1 ta thu được \(\left(\overrightarrow{AC},\overrightarrow{CB}\right)=120^o\), \(\left(\overrightarrow{AB},\overrightarrow{CB}\right)=60^o\), \(\left(\overrightarrow{OA},\overrightarrow{BC}\right)=90^o\), \(\left(\overrightarrow{OC},\overrightarrow{BC}\right)=30^o\), \(\left(\overrightarrow{OA},\overrightarrow{BO}\right)=60^o\).

Suy ra 

\(\overrightarrow{AC}.\overrightarrow{CB}=\left|\overrightarrow{AC}\right|.\left|\overrightarrow{CB}\right|.\cos\left(\overrightarrow{AC},\overrightarrow{CB}\right)=1.1.\cos120^o=-\dfrac{1}{2}\);

\(\overrightarrow{AB}.\overrightarrow{CB}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{CB}\right|.\cos\left(\overrightarrow{AB},\overrightarrow{CB}\right)=1.1.\cos60^o=\dfrac{1}{2}\);

\(\overrightarrow{OA}.\overrightarrow{BC}=\left|\overrightarrow{OA}\right|.\left|\overrightarrow{BC}\right|.\cos\left(\overrightarrow{OA},\overrightarrow{BC}\right)=\dfrac{\sqrt{3}}{3}.1.\cos90^o=0\);

\(\overrightarrow{OC}.\overrightarrow{BC}=\left|\overrightarrow{OC}\right|.\left|\overrightarrow{BC}\right|.\cos\left(\overrightarrow{OC},\overrightarrow{BC}\right)=\dfrac{\sqrt{3}}{3}.1.\cos30^o=\dfrac{1}{2}\);

\(\overrightarrow{OA}.\overrightarrow{BO}=\left|\overrightarrow{OA}\right|.\left|\overrightarrow{BO}\right|.\cos\left(\overrightarrow{OA},\overrightarrow{BO}\right)=\dfrac{\sqrt{3}}{3}.\dfrac{\sqrt{3}}{3}.\cos60^o=\dfrac{1}{6}\).

3. Biểu thức tọa độ và tính chất của tích vô hướng

Biểu thức tọa độ

Tích vô hướng của hai vectơ \(\overrightarrow{u}\left(x;y\right)\) và \(\overrightarrow{v}\left(x';y'\right)\) được tính theo công thức:

 \(\overrightarrow{u}.\overrightarrow{v}=xx'+yy'\).

Nhận xét

• Hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\) vuông góc với nhau khi và chỉ khi \(xx'+yy'=0\).
• Bình phương vô hướng của \(\overrightarrow{u}\left(x;y\right)\) là \(\overrightarrow{u}^2=x^2+y^2\).
• Nếu \(\overrightarrow{u}\ne\overrightarrow{0}\) và \(\overrightarrow{v}\ne\overrightarrow{0}\) thì \(\cos\left(\overrightarrow{u},\overrightarrow{v}\right)=\dfrac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}=\dfrac{xx'+yy'}{\sqrt{x^2+y^2}.\sqrt{x'^2+y'^2}}\).

Tính chất

Với ba vectơ \(\overrightarrow{u}\), \(\overrightarrow{v}\), \(\overrightarrow{w}\) bất kì và mọi số thực \(k\), ta có: 

• Tính chất giao hoán: \(\overrightarrow{u}.\overrightarrow{v}=\overrightarrow{v}.\overrightarrow{u}\);
• Tính chất phân phối đối với phép cộng vectơ: \(\overrightarrow{u}.\left(\overrightarrow{v}+\overrightarrow{w}\right)=\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{u}.\overrightarrow{w}\);
• Tính chất kết hợp đối với phép nhân với số: \(\left(k\overrightarrow{u}\right).\overrightarrow{v}=k\left(\overrightarrow{u}.\overrightarrow{v}\right)=\overrightarrow{u}.\left(k\overrightarrow{v}\right)\).

Chú ý. Từ các tính chất trên, ta có: 

• \(\overrightarrow{u}.\left(\overrightarrow{v}-\overrightarrow{w}\right)=\overrightarrow{u}.\overrightarrow{v}-\overrightarrow{u}.\overrightarrow{w}\) (tính chất phân phối đối với phép trừ);
• \(\left(\overrightarrow{u}+\overrightarrow{v}\right)^2=\overrightarrow{u}^2+2\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{v}^2\); \(\left(\overrightarrow{u}-\overrightarrow{v}\right)^2=\overrightarrow{u}^2-2\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{v}^2\);
• \(\left(\overrightarrow{u}+\overrightarrow{v}\right).\left(\overrightarrow{u}-\overrightarrow{v}\right)=\overrightarrow{u}^2-\overrightarrow{v}^2\).

Ví dụ 3: Trong mặt phẳng tọa độ \(Oxy\) cho hai điểm \(A\left(1;2\right)\) và \(B\left(5;0\right)\). 

a) Chứng minh \(OA\) vuông góc với \(AB\).

b) Gọi \(M\) là trung điểm \(AB\). Tính số đo góc \(\widehat{AOM}\).

Giải

a) Ta có \(\overrightarrow{OA}=\left(1-0;2-0\right)=\left(1;2\right)\), \(\overrightarrow{AB}=\left(5-1;0-2\right)=\left(4;-2\right)\).

Suy ra \(\overrightarrow{OA}.\overrightarrow{AB}=1.4+2.\left(-2\right)=0\).

Do các vectơ \(\overrightarrow{OA}\), \(\overrightarrow{AB}\) đều khác vectơ-không nên \(OA\perp BC\).

b) Do \(M\) là trung điểm của \(AB\) nên \(M\left(3;1\right)\). 

Suy ra \(\overrightarrow{OM}=\left(3;1\right)\), \(OM=\left|\overrightarrow{OM}\right|=\sqrt{3^2+1^2}=\sqrt{10}\).

\(\left|\overrightarrow{OA}\right|=\sqrt{1^2+2^2}=\sqrt{5}\).

Do đó \(\cos\left(\overrightarrow{OA},\overrightarrow{OM}\right)=\dfrac{\overrightarrow{OA}.\overrightarrow{OM}}{\left|\overrightarrow{OA}\right|.\left|\overrightarrow{OM}\right|}=\dfrac{1.3+2.1}{\sqrt{5}.\sqrt{10}}=\dfrac{1}{\sqrt{2}}\).

Suy ra \(0^o< \left(\overrightarrow{OA},\overrightarrow{OM}\right)< 90^o\) và do đó \(\widehat{AOM}=\left(\overrightarrow{OA},\overrightarrow{OM}\right)=45^o\).