Hàm số và đồ thị SVIP

1. HÀM SỐ. TẬP XÁC ĐỊNH VÀ TẬP GIÁ TRỊ CỦA HÀM SỐ

Giả sử \(x\) và \(y\) là hai đại lượng biến thiên và \(x\) nhận giá trị thuộc tập số \(D.\)

Nếu với mỗi giá trị \(x\) thuộc \(D\) ta xác định được một và chỉ một giá trị tương ứng của \(y\) thuộc tập hợp số thực \(ℝ\) thì ta có một hàm số.

Ta gọi \(x\) là biến số và \(y\) là hàm số của \(x\).

Tập hợp \(D\) gọi là tập xác định của hàm số.

Tập hợp \(T\) gồm tất cả các giá trị \(y\) (tương ứng với \(x\) thuộc \(D\)) gọi là tập giá trị của hàm số.

Chú ý.

- Ta thường dùng kí hiệu \(f\left(x\right)\) để chỉ giá trị \(y\) tương ứng với \(x\) và được viết tắt là \(y=f\left(x\right).\)

- Một hàm số có thể được cho bằng bảng, bằng biểu đồ hoặc bằng công thức.

Khi cho hàm số bằng công thức \(y=f\left(x\right)\) mà không chỉ rõ tập xác định của nó thì ta quy ước:

Tập xác định của hàm số là tập hợp tất cả các số thực \(x\) sao cho biểu thức \(f\left(x\right)\) có nghĩa.

Ví dụ. Tìm tập xác định của các hàm số sau:

a) \(y=\sqrt{5-3x}\);               b) \(y=\dfrac{3}{x+4}\).

Giải

a) Biểu thức \(\sqrt{5-3x}\) có nghĩa khi \(5-3x\ge0\), hay \(x\le\dfrac{5}{3}\).

Vậy tập xác định của hàm số đã cho là \(D=(-\infty;\dfrac{5}{3}].\)

b) Biểu thức \(\dfrac{3}{x+4}\) có nghĩa khi \(x+4\ne0\), hay \(x\ne-4\).

Vậy tập xác định của hàm số đã cho là \(D=\mathbb{R}\setminus \left \{ -4 \right \}\).

2. ĐỒ THỊ HÀM SỐ

Cho hàm số \(y=f\left(x\right)\) có tập xác định \(D\).

Trên mặt phẳng tọa độ \(Oxy\), đồ thị \(\left(C\right)\) của hàm số là tập hợp tất cả các điểm \(M\left(x;y\right)\) với \(x\in D\) và \(y=f\left(x\right)\).

Ví dụ.

• Đồ thị hàm số \(f\left(x\right)=x+1.\)

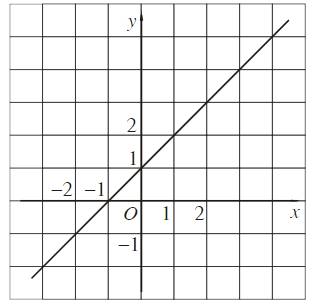
• Hàm số \(g\left(x\right)=\dfrac{1}{2}x^2.\)

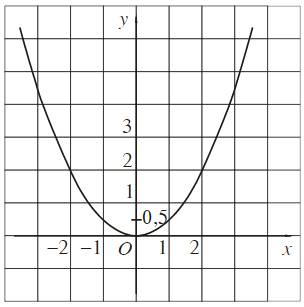
Chú ý: Điểm \(M\left(x_M;y_M\right)\) thuộc đồ thị hàm số \(y=f\left(x\right)\) khi và chỉ khi \(x_M\in D\) và \(y_M=f\left(x_M\right).\)

3. HÀM SỐ ĐỒNG BIẾN, HÀM SỐ NGHỊCH BIẾN

Cho hàm số \(y=f\left(x\right)\) xác định trên khoảng \(\left(a;b\right).\)

• Hàm số \(y=f\left(x\right)\) đồng biến trên khoảng \(\left(a;b\right)\) nếu:\(\forall x_1,x_2\in\left(a;b\right),x_1< x_2\Rightarrow f\left(x_1\right)< f\left(x_2\right).\)
•  Hàm số \(y=f\left(x\right)\) nghịch biến trên khoảng \(\left(a;b\right)\) nếu:\(\forall x_1,x_2\in\left(a;b\right),x_1< x_2\Rightarrow f\left(x_1\right)>f\left(x_2\right).\)

 

Nhận xét:

• Hàm số đồng biến (tăng) trên khoảng \(\left(a;b\right)\)thì đồ thị của nó có dạng đi lên từ trái sang phải.
• Hàm số nghịch biến (giảm) trên khoảng \(\left(a;b\right)\) lthì đồ thị của nó có dạng đi xuống từ trái sang phải.

Ví dụ. Xét tính đồng biến, nghịch biến của hàm số \(y=-2x+1\) trên \(ℝ\).

Giải

Xét hai số bất kì \(x_1,x_2\inℝ\) sao cho \(x_1< x_2.\)

Ta có \(x_1< x_2\Rightarrow-2x_1>-2x_2\Rightarrow-2x_1+1>-2x_2+1\)

hay \(f\left(x_1\right)>f\left(x_2\right)\).

Vậy hàm số đã cho nghịch biến trên \(ℝ\).