Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Hàm số bậc hai SVIP
1. HÀM SỐ BẬC HAI
Hàm số bậc hai theo biến \(x\) là hàm số được cho bởi công thức có dạng \(y=ax^2+bx+c,\) trong đó \(a,b,c\) là các hằng số và \(a\ne0.\)
Tập xác định của hàm số bậc hai là \(ℝ\).
Ví dụ: trong các hàm số sau, hàm số nào là hàm số bậc hai?
a)\(y=3x^3-2x+1\);
b)\(y=-2x^2+x+3\);
c)\(y=\dfrac{1}{x^2}-\dfrac{2}{x}+1\).
Giải
Hàm số \(y=-2x^2+x+3\) là hàm số bậc hai có hệ số của \(x^2\) là \(-2\), hệ số của \(x\) là \(1\), hệ số tự do là \(3.\)
Hàm số \(y=3x^3-2x+1\) và \(y=\dfrac{1}{x^2}-\dfrac{2}{x}+1\) không phải là hàm số bậc hai.
2. ĐỒ THỊ HÀM SỐ BẬC HAI
Trong mặt phẳng tọa độ \(Oxy\), đồ thị hàm số bậc hai \(y=ax^2+bx+c\left(a\ne0\right)\) là một parabol \(\left(P\right):\)
- Có đỉnh \(S\) với hoành độ \(x_S=-\dfrac{b}{2a}\), tung độ \(y_S=-\dfrac{\Delta}{4a};\)
- Bề lõm quay lên trên nếu \(a>0,\) quay xuống dưới nếu \(a< 0;\)
- Căt trục tung tại điểm có tung độ bằng \(c\), tức là đồ thị đi qua điểm có tọa độ \(\left(0;c\right).\)
Chú ý:
a) Nếu \(b=2b'\) thì \(\left(P\right)\) có đỉnh \(S\left(-\dfrac{b'}{a};-\dfrac{\Delta}{a}\right).\)
b) Nếu phương trình \(ax^2+bx+c=0\) có hai nghiệm \(x_1,x_2\) thì đồ thị hàm số bậc hai \(y=ax^2+bx+c\left(a\ne0\right)\) cắt trục hoành tại hai điểm lần lượt có hoành độ là hai nghiệm này.
Cách vẽ đồ thị hàm số bậc hai \(y=ax^2+bx+c\left(a\ne0\right)\):
1. Xác định tọa độ đỉnh \(S\left(-\dfrac{b}{2a};-\dfrac{\Delta}{4a}\right);\)
2. Vẽ trục đối xứng \(d\) là đường thẳng \(x=-\dfrac{b}{2a}\);
3. Xác định một số điểm đặc biệt như: giao điểm của đồ thị với trục tung (có tọa độ \(A\left(0;c\right)\)), giao điểm đồ thị với trục hoành (nếu có), điểm đối xứng với điểm \(A\) qua trục đối xứng \(d\) là điểm \(B\left(-\dfrac{b}{a};c\right).\)
4. Vẽ parabol có đỉnh \(S\), trục đối xứng \(d\), đi qua các điểm tìm được.
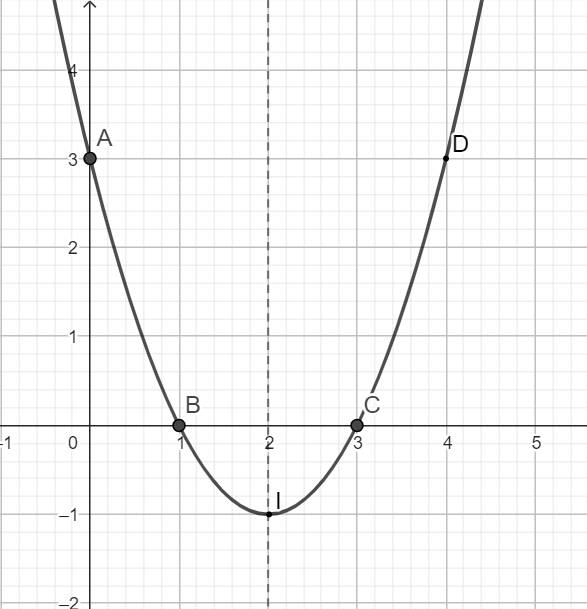
Ví dụ. Vẽ đồ thị hàm số \(y=x^2-4x+3\).
Giải
Tọa độ đỉnh \(I\left(2;-1\right)\);
Trục đối xứng \(x=2\).
Giao điểm của parabol với trục tung là \(A\left(0;3\right)\), giao điểm của parabol với trục hoành là \(B\left(1;0\right)\) và \(C\left(3;0\right)\).
Điểm đối xứng với điểm \(A\left(0;3\right)\) qua trục đối xứng \(x=2\) là \(D\left(4;3\right)\).
Vẽ parabol qua các điểm được xác định như trên, ta được đồ thị hàm số \(y=x^2-4x+3\).
3. SỰ BIẾN THIÊN CỦA HÀM SỐ BẬC HAI
| Với \(a>0\) | Với \(a< 0\) |
|
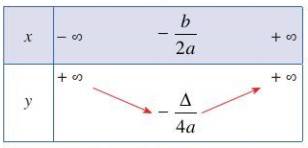
Hàm số nghịch biến trên khoảng \(\left(-\infty;-\dfrac{b}{2a}\right);\) Hàm số đồng biến trên khoảng \(\left(-\dfrac{b}{2a};+\infty\right);\) \(-\dfrac{\Delta}{4a}\) là giá trị nhỏ nhất của hàm số. Bảng biến thiên:
Hàm số có tập giá trị là \(T=[-\dfrac{\Delta}{4a};+\infty).\) |
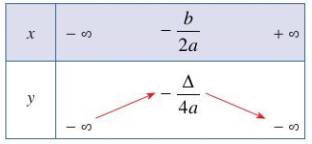
Hàm số đồng biến trên khoảng \(\left(-\infty;-\dfrac{b}{2a}\right);\) Hàm số nghịch biến trên khoảng \(\left(-\dfrac{b}{2a};+\infty\right);\) \(-\dfrac{\Delta}{4a}\) là giá trị lớn nhất của hàm số. Bảng biến thiên:
Hàm số có tập giá trị là \(T=(-\infty;-\dfrac{\Delta}{4a}].\) |
Bạn có thể đăng câu hỏi về bài học này ở đây