Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Đồ thị hàm số bậc hai SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Kiến thức cần nhớ
+ Đồ thị hàm số bậc hai $y = ax^2 + bx + c$ là một parabol, với $a \ne 0$.
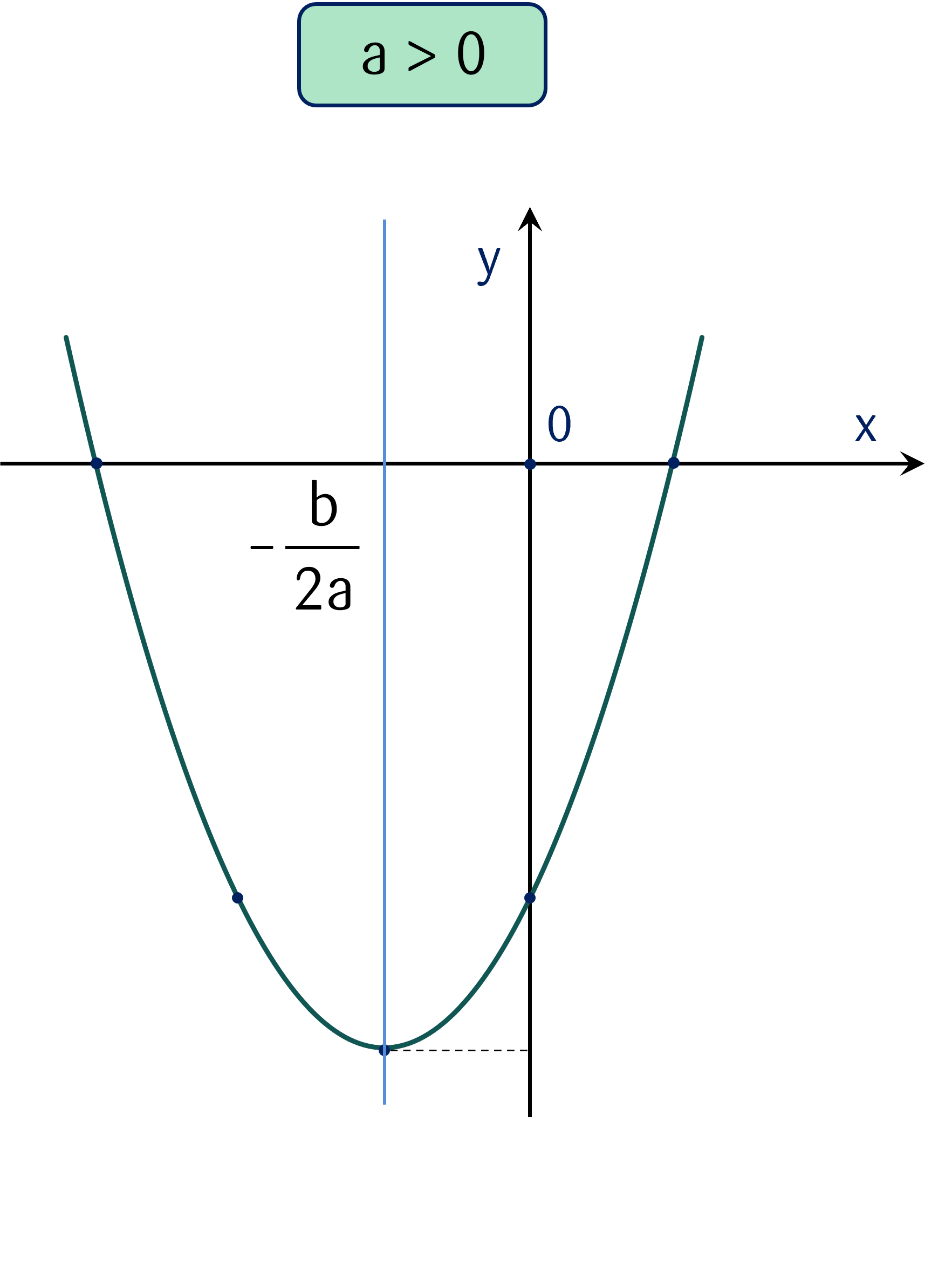 |
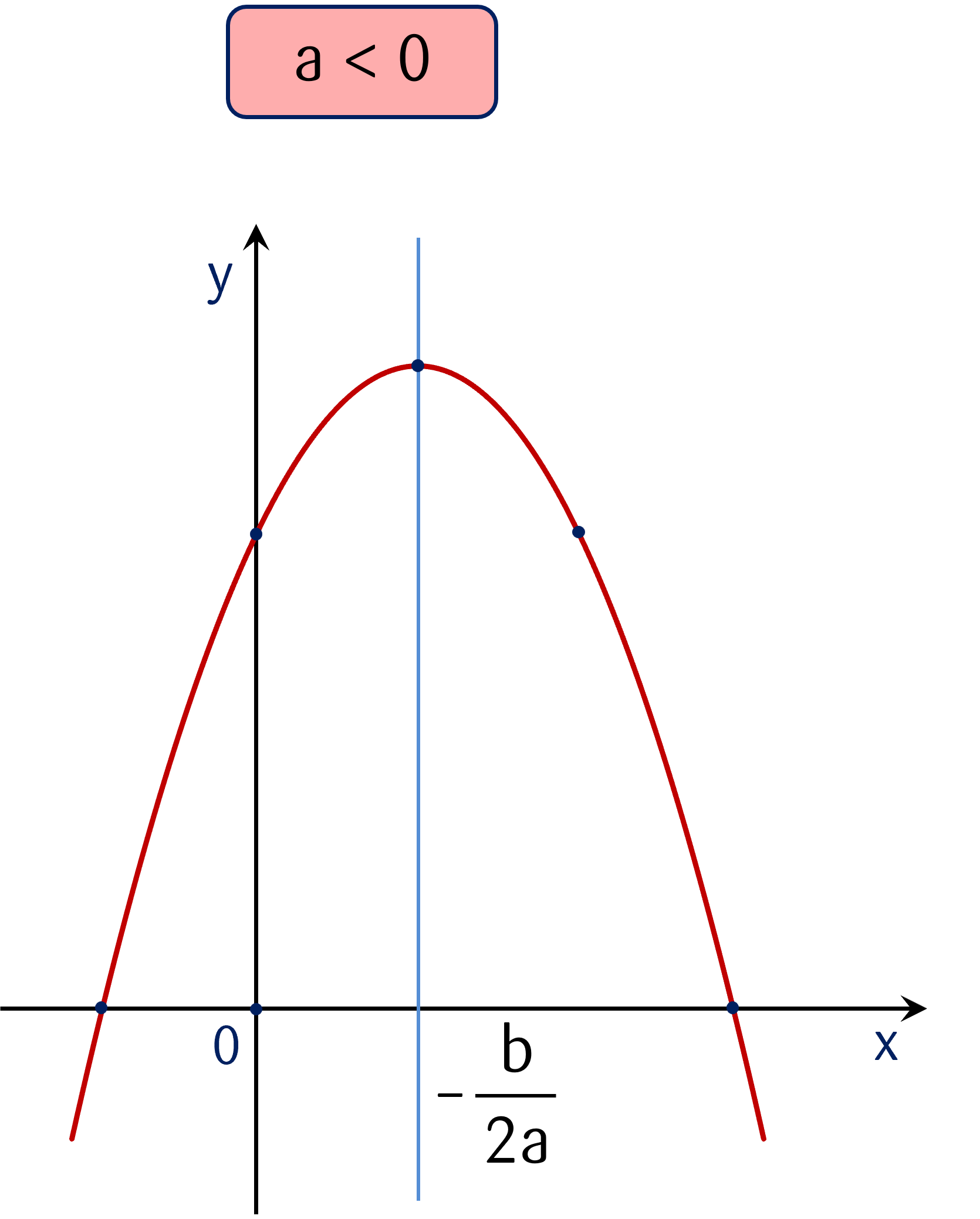 |
+ Tọa độ đỉnh $I\left(-\dfrac b{2a};-\dfrac {\Delta}{4a} \right)$ với $\Delta = b^2 - 4ac$;
+ Trục đối xứng $x = -\dfrac b{2a}$.
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
Hàm số y=ax2 với a=0 có là hàm số bậc hai hay không?
- Không
- Có
Câu 2 (1đ):
Xét hàm số y=f(x)=x2+2x−3. Điền số thích hợp để hoàn thiện bảng:
| x | −3 | −2 | −1 | 0 | 1 |
| y | 0 | −3 |
Câu 3 (1đ):
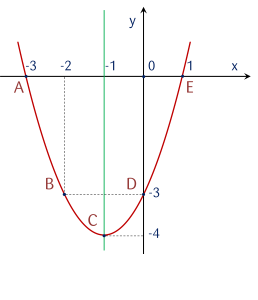
Quan sát đồ thị hàm số trên. Điểm B(−2;−3) và D(0;−3) là hai điểm đối xứng nhau qua
trục Ox.
đường thẳng y=−1.
đường thẳng x=−1.
trục Oy.
Câu 4 (1đ):
Cho hàm số y=x2−2x−3, trrong đó a=1; b=−2 và c=−3.
Biệt thức Δ=b2−4ac= .
Câu 5 (1đ):
Phương trình hoành độ giao điểm x2−2x−3=0 có nghiệm
x=−2; x=3.
x=−1; x=3.
x=−3; x=1.
x=−1; x=2.
Câu 6 (1đ):
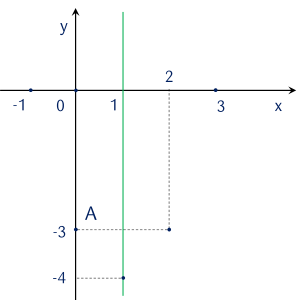
Điểm đối xứng của điểm A(0;−3) qua trục đối xứng x=1 là
(2;−3).
(2;0).
(−3;2).
(1;−3).
Câu 7 (1đ):
Quan sát đồ thị hàm số y=f(x) sau:
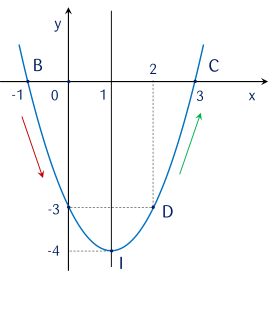
Hàm số f(x) nghịch biến trên khoảng
(−∞;1).
(0;+∞).
(−∞;0).
(1;+∞).
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- [âm nhạc]
- ở các lớp dưới chúng ta có đề cập tới
- hàm số y = a bình với a khác 0 vậy đó có
- phải là một hàm số bậc hai hay không
- chính xác đó là một hàm số bậc hai và
- chúng ta có các dạng đồ thị của hàm số y
- = a bình như thế này
- khi mà a lớn hơn 0 thì đồ thị hàm số sẽ
- có dạng như Đường Màu Xanh bầy lõm sẽ
- hướng lên
- còn A nhỏ hơn 0 là trường hợp Thứ hai
- này đồ thị hàm số là đường parabol màu
- đỏ có bề lõm hướng xuống
- vậy thì đồ thị của hàm số bậc hai Nói
- chung có cùng dấu đồ thị của hàm số y =
- ax² với a khác 0 nữa hay không Chúng ta
- sẽ đến với nội dung của phân số 2 nhé
- Thấy sẽ xét hàm số
- y = x² + 2x - 3 các bạn sẽ điền các số
- thích hợp để hoàn thiện bảng sau đây
- với x bằng -3 thì thay vào đây ta được
- âm Mai Bình là 9 này cộng 2 nhân 3 là -6
- - 3 ta được 0 tương tự thay -2 vào ta sẽ
- có y = -3
- chính xác X bằng -1 thì y bằng âm 4 x =
- 0 y = -3 và x = 1 y = 0 như vậy ta có 5
- điểm
- chính là 5 điểm thuộc vào đồ thị của hàm
- số y = FX
- thầy gọi đó là các điểm A B C D và E và
- ta sẽ biểu diễn Chúng ở trên hệ trục tọa
- độ Oxy
- đầu tiên là điểm A có tọa độ -3 0 này
- điểm B có tọa độ -2 -3 điểm c có tọa độ
- -4 -1 tiếp theo điểm d có tọa độ 0 - 3
- điểm E có tọa độ
- không Và khi các bạn vẽ một đường cong
- đi qua 5 điểm trên ta sẽ thu được đường
- màu đỏ chính là đồ thị của hàm số y = fx
- bằng x bình cộng 2x - 3 cách vẽ đồ thị
- hàm số bậc hai nói chung thì cũng cần
- tới 5 điểm như vẽ đồ thị hàm số y = ax
- bình trong đồ thị hàm số này chúng ta
- vẫn chú ý vào bề lõm trong trường hợp cụ
- thể này thì đồ thị hàm số có bầy lõm
- quay lên tọa độ điểm thấp nhất hãy chính
- là tọa độ đỉnh là điểm C có tọa độ -1 -4
- và trục đối xứng là Đường Màu Xanh Thay
- thể hiện ở trên đồ thị này chính là
- đường thẳng x = -1 nhưng đồ thị này có
- bề rộng quay lên do hệ số a hệ số của x
- bình bằng 1 lớn hơn 0 vậy tiếp theo thầy
- sẽ lấy thêm một trường hợp nữa đó là đồ
- thị hàm số y bằng trừ x bình cộng 2x + 3
- vậy cách vẽ đồ thị của các hàm số này
- Lát nữa chúng ta để tìm hiểu cụ thể cũng
- là lấy 5 điểm nhưng 5 điểm đó được chọn
- như thế nào còn ở đây thầy sẽ cho Sẵn đồ
- thị của hàm số đó chính là đường cong
- màu đỏ đi qua các điểm các bạn đang thấy
- được trên màn hình
- trường hợp này là a lớn hơn 0 trường hợp
- thứ hai là A nhỏ hơn 0 chúng ta sẽ thấy
- được sự khác biệt về trục đối xứng tọa
- độ điểm thấp hay cao nhất cũng như bề
- lõm của hai đồ thị trên đầu tiên là về
- bề lõm dễ dàng nhận thấy nhất khi a lớn
- hơn 0 bõm sẽ hướng lên Còn khi a nhỏ hơn
- 0 thì bề lõm sẽ hướng xuống khi bề lõm
- hướng lên thì ta sẽ có điểm thấp nhất
- trên đồ thị hàm số và tọa độ điểm thấp
- nhất trong trường hợp này sẽ là -1 -4
- nhưng khi đồ thị hàm số có bề lõm hướng
- xuống thì trên đồ thị lại xuất hiện điểm
- có tọa độ cao nhất chứ không có điểm có
- tọa độ thấp nhất nữa nhé và điểm này sẽ
- có
- công cụ là 14 chung đối xứng của đồ thị
- hàm số thứ nhất sẽ là đường màu xanh lá
- cây chính là x = -1 còn đồ thị hàm số
- thứ hai này là đường thẳng có phương
- trình x = 1 Vậy qua cả hai trường hợp
- này liệu chúng ta có mối liên hệ gì giữa
- trục đối xứng tọa độ điểm thấp nhất cao
- nhất hay chính là tọa độ đỉnh cùng với
- bề lõm của các đồ thị Hay không các bạn
- sẽ quan sát vào hàm số thứ nhất thay
- biến đổi như sau x² + 2x - 3 ta sẽ thêm
- bớt để xuất hiện hằng đẳng thức x + 1
- tất cả bình còn lại trừ đi 4 tới đây nếu
- ta đánh giá x + 1 tất cả bình thì luôn
- lớn hơn hoặc bằng 0 với mọi x trừ đi 4
- sẽ lớn hơn hoặc bằng âm 4 với mọi x hay
- nói cách khác hàm số FX này sẽ đạt giá
- trị lớn nhất là âm 4 khi mà X = -1 âm 4
- âm 1 lại tương ứng với hoành độ và tung
- độ của đỉnh X = -1 thì lại là trục đối
- xứng của đồ thị hộp số và nó cũng chính
- là ý tưởng để chúng ta nhận xét các tính
- chất của đồ thị hàm số ở trong công thức
- tổng quát là y = a bình cộng b cộng c
- với a khác 0 khi đó thầy sẽ biến đổi y =
- 2 bình + b + c bằng cách đặt a làm nhân
- tử chung bên trong sẽ còn là x bình cộng
- 2 nhân b phần 2A Nhân X thành nhân 2 và
- chia 2 rồi cộng với b phần 2A tất cả
- bình chính bằng b bình phần 4A bình cộng
- thêm thì ta phải trừ đi b bình phần 4A
- các bạn chú ý ở đây là 4A nhé bởi vì b
- bình phần 4A Bình nhân với a bên ngoài
- nữa thì A với a dưới mẫu rút gọn ta còn
- lại phần này và cuối cùng là cộng với c
- phần thẻ gạch này ta sử dụng hằng đẳng
- thức M + N tất cả bình phương để có a
- nhân với x cộng b phần 2A tất cả bình
- phương
- phần Phía Sau Thầy quy đồng thành b bình
- trừ 4ac phần 4A và với có thể Khoanh
- tròn ở đây ta tiếp tục đặt b bình trừ
- 4ac là Delta biểu thức Delta khi đó
- Y sẽ trở thành a nhân với x + b/2 a tất
- cả bình trừ đi delta phần 4A và tương tự
- như trong ví dụ trước ta sẽ xét phần
- bình phương này luôn lớn hơn hoặc bằng 0
- với mọi x khi đó ta sẽ so sánh được y
- với một biểu thức không chứa x nhưng ở
- đây phải phụ thuộc vào giá trị vào dấu
- của a nếu trong trường hợp a lớn hơn 0
- thì a nhân với bình phương này sẽ lớn
- hơn hoặc bằng 0 khi đó FX sẽ lớn hơn
- hoặc bằng - Delta trên 4A với mọi x dấu
- bằng xảy ra khi mà X bằng trừ b phần 2A
- nhé Trường hợp A lớn 0 thì đồ thị hàm số
- sẽ có dạng như thế này trong đó điểm I
- có tọa độ là trừ b phần 2A tung độ trừ
- Delta trên 4A sẽ là điểm cao thấp nhất
- trên đồ thị hàm số này
- parabol sẽ có bề lõm quay lên trên do a
- lớn hơn 0 và trục đối xứng ta xác định
- được chính là đường thẳng x =
- -b/2a
- Còn trong trường hợp A âm tức là parabol
- sẽ quay bề lõm xuống dưới như thế này
- thì FX khi đó lại nhỏ hơn hoặc bằng -
- delta/4a với mọi x điểm y hay chính là
- đỉnh I của parabol trên là điểm cao nhất
- trên đồ thị hàm số và trục đối xứng vẫn
- là đường thẳng trừ B trên 2A như vậy
- trong trường hợp tổng quát tùy vào giá
- trị của a a Dương thì bề lõm sẽ quay lên
- đỉnh là điểm thấp nhất trong trường hợp
- A nhỏ hơn 0 thì đỉnh là điểm cao nhất
- của đồ thị hàm số
- parabol có 7 lõm quay xuống dưới và
- trong cả hai trường hợp này ta đều xác
- định được trục đối xứng là đường thẳng x
- thầy sẽ tổng kết nội dung lý thuyết này
- như sau đôi khi hàm số bậc hai y = a
- bình cộng bx + c với a khác 0 là 1
- Parabol trong trường hợp a lớn hơn 0
- parabol sẽ có dạng như thế này còn đây
- là trong trường hợp nhóm không ta phân
- biệt được a lớn hơn 0 b lõm sẽ quay lên
- A nhỏ hơn 0 b lõm của parabol quay xuống
- tọa độ đỉnh của đồ thị hàm số bậc hai là
- trừ b phần 2A trừ delta phần 4A trong đó
- trục đối xứng là đường thẳng x = -b/2a
- đây chính là những nội dung quan trọng
- mà các bạn phải ghi nhớ ở trong phần số
- 2 về đồ thị của hàm số bậc hai vận dụng
- nội dung lý thuyết này chúng ta sẽ đến
- với câu hỏi hỏi chấm 1 yêu cầu vẽ đồ thị
- hàm số y = x bình trừ 2X - 3 như ở phần
- trước thầy cũng nói rồi cách vẽ đồ thị
- hàm số chúng ta sẽ đề cập ở phần sau khi
- mà ta đã tìm công cụ về tọa độ đỉnh và
- trục đối xứng rồi thì các em sẽ biết
- cách xác định 5 điểm để vẽ đồ thị hàm số
- này sao cho nhanh chóng nhất đầu tiên là
- các bạn phải xác định được các hệ số A B
- C từ ở đây a sẽ bằng 1 b là âm 2 c là âm
- 3 từ đó ta sẽ tính delta
- với công thức Delta bằng b bình trừ 4ac
- thì ta sẽ tính được delta ở đây là 16 từ
- đó các bạn sẽ xác định được cho thầy tọa
- độ đỉnh thay đen ta bằng 16 và công thức
- ta có trừ b phần 2A là -2/2 bằng 1 trừ
- delta phần 4A là
- -16/4 tức là -4 vậy tọa độ đỉnh sẽ là 1
- âm 4 tiếp theo trục đối xứng dễ dàng xác
- định được là đường thẳng x = 1 các điểm
- đặc biệt tiếp theo các điểm tiếp theo
- thì các bạn sẽ xác định cũng qua giao
- điểm với các trục tọa độ đầu tiên là với
- trục Oy thì ta sẽ thay chính xác ta thay
- x = 0 và tìm được y = -3 như vậy điểm A
- có tọa độ không âm 3 là điểm tiếp theo
- giao điểm với trục hoành thì các bạn sẽ
- cho x bình trừ 2X - 3 = 0 và giải phương
- trình bậc 2 này
- với hai nghiệm là -1 và 3 thì chúng ta
- sẽ có hai điểm điểm B tọa độ -1 0 và
- điểm C tọa độ 3; 0 thuộc vào đồ thị hàm
- số như vậy các bạn đã có 1 2 3 và 4 điểm
- điểm cuối cùng ta sẽ lấy điểm đối xứng
- với A
- qua trục đối xứng
- A có tọa độ 0 -3 đây đối xứng qua đường
- thẳng Màu xanh sẽ là điểm D của tọa độ
- là 2 -3 như vậy chúng ta đã xác định
- được 5 điểm a b c d và I từ đó chúng ta
- sẽ vẽ một đường cong đi qua 5 điểm trên
- thì parabol màu đỏ chính là đồ thị của
- hàm số y = x² - 2x - 3 nhé
- đó là cách kèm vẽ đồ thị của một hàm số
- bậc hai nói chung
- dựa vào đồ thị hàm số bậc 2 các bạn sẽ
- trả lời cho thầy câu hỏi chấm 2 là quan
- sát đồ thị và xác định các khoảng đồng
- biến nghịch biến của hàm số đó
- ở bài học trước chúng ta đã xác định rồi
- với đồ thị hàm số tính theo chiều từ
- trái sang phải nếu như đồ thị hàm số có
- hướng đi xuống hàm số sẽ nghịch biến
- trên khoảng tương ứng con đồ thị mà đi
- lên thì hàm số đồng biến vậy Ở đây hàm
- số sẽ nghịch biến ở trên khoảng
- với tọa độ đỉnh là 1 âm 4 thì ta sẽ xét
- có đủ bổ ích nhé tính từ âm vô cùng cho
- đến điểm có hoành độ 1 thì đồ thị hàm số
- luôn Có Chiều đi xuống hay hàm số nghịch
- biến trên khoảng từ âm vô cùng đến 1 còn
- lại khoảng từ 1 cho đến dương vô cùng
- thì hàm số sẽ đồng biến do đó tại đỉnh
- của parabol sẽ là vị trí mà hàm số sẽ
- chuyển từ đồng biến sang nghịch biến
- hoặc ngược lại
OLMc◯2022

Bạn có thể đánh giá bài học này ở đây