GTLN, GTNN - Cho f'(x), một số bài toán VD, VDC SVIP

Cho hàm số $f(x)$ có đạo hàm $f'(x) = x(x + 1)(x - 2)^{2}$ với mọi $x\mathbb{\in R}.$ Giá trị nhỏ nhất của hàm số $f(x)$ trên đoạn $\lbrack - 1;2\rbrack$ là

Cho hàm số $f(x)$ có đạo hàm $f'(x)$ liên tục trên $\mathbb{R}$ và đồ thị của hàm số $f'(x)$ trên đoạn $\lbrack - 2;6\rbrack$ như hình vẽ bên. Mệnh đề nào sau đây đúng?

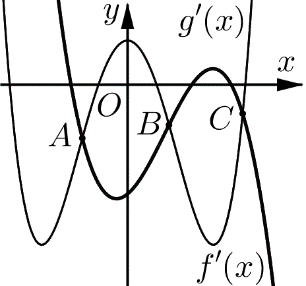
Cho hai hàm số $y = f(x)$ và $y = g(x)$ liên tục trên $\mathbb{R}$ có đồ thị hàm số $y = f'(x)$ là đường cong nét đậm và $y = g'(x)$ là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm $A,B,C$ của đồ thị $y = f'(x)$ và $y = g'(x)$ trên hình vẽ lần lượt có hoành độ là $a,b,c.$ Giá trị nhỏ nhất của hàm số $h(x) = f(x) - g(x)$ trên đoạn $\lbrack a;c\rbrack$ bằng

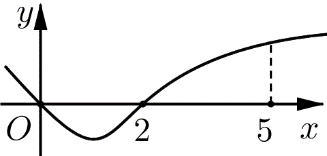
Cho hàm số $y = f(x).$ Đồ thị hàm số $y = f'(x)$ như hình bên. Biết rằng $f(0) + f(3) = f(2) + f(5).$ Giá trị nhỏ nhất và giá trị lớn nhất của$f(x)$ trên đoạn$\lbrack 0;5\rbrack$ lần lượt là

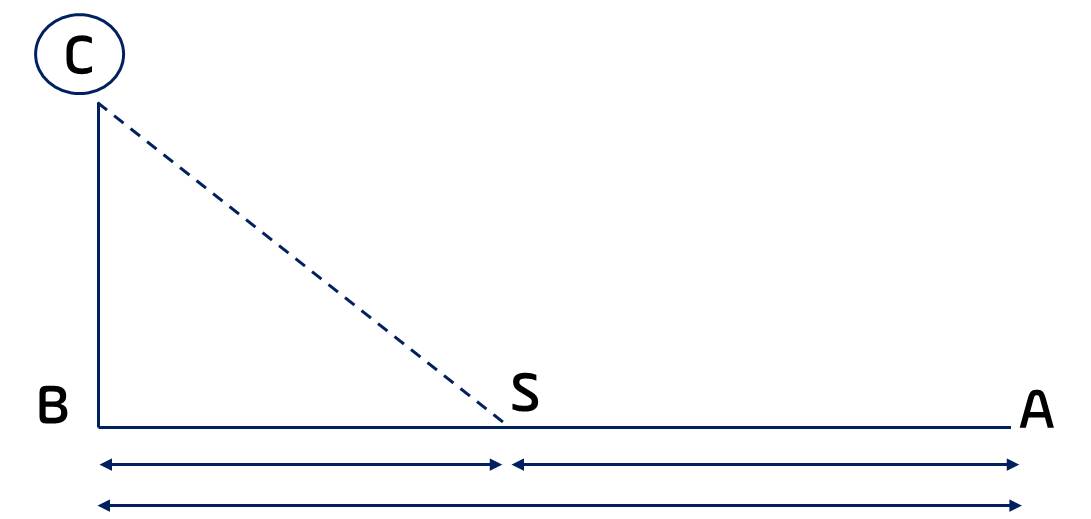
Một đường dây điện được nối từ một nhà máy điện ở $A$ đến một hòn đảo ở $C$ khoảng cách ngắn nhất từ $C$ đến $B$ là $1$ km. Khoảng cách từ $B$ đến $A$ là $4$ km. Mỗi km dây điện đặt dưới nước là mất $5000$ USD, còn đặt dưới mặt đất mất $3000$ USD. Hỏi điểm $S$ trên bờ cách $A$ bao nhiêu km để khi mắc dây điện từ $A$ qua $S$ rồi đến $C$ là ít tốn kém nhất?

Gọi ${S}$ là tập tất cả các giá trị thực của tham số${m}$ sao cho giá trị giá trị lớn nhất của hàm số ${f}{(}{x}{)}{=}\left| {x}^{{4}}{-}{8}{x}^{{2}}{+ m} \right|$ trên đoạn $\left\lbrack {-}{1;3} \right\rbrack$ bằng ${18}$. Tổng tất cả các phần tử của ${S}$ bằng

Cho hàm số $f(x)$, biết $y=f^{\prime}(x)$ có đồ thị như hình vẽ.

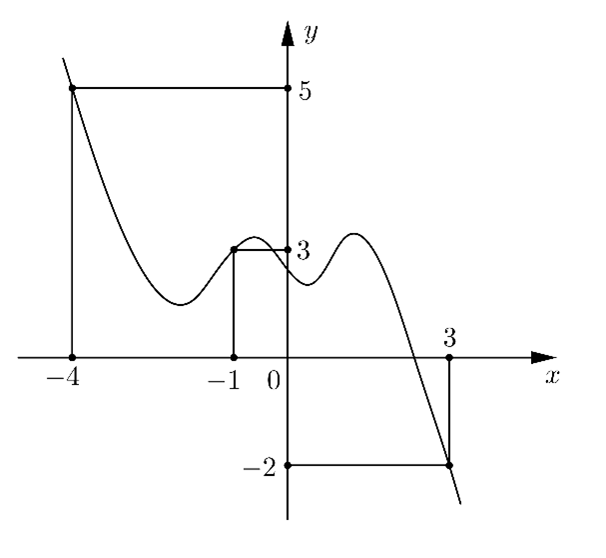
Gọi giá trị nhỏ nhất của hàm số $g(x)=2 f(x)+(x-1)^{2}$ trên đoạn $[-4 ; 3]$ là $m$. Kết luận nào sau đây đúng?

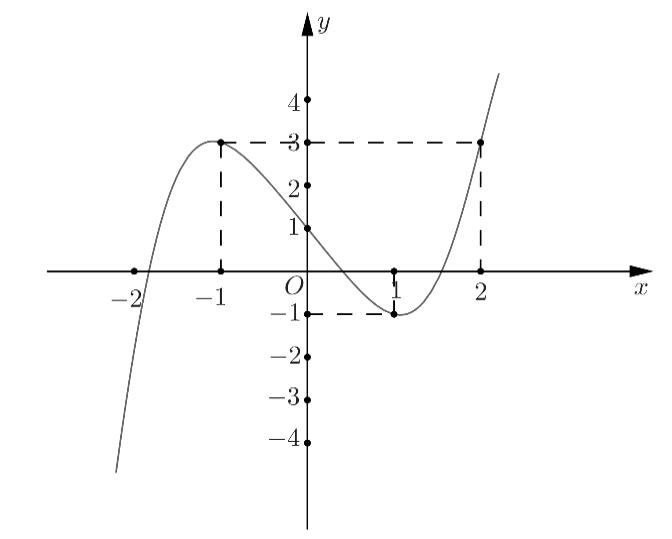
Cho hàm số $f(x)$ là hàm đa thức bậc 3 và có đồ thị như hình vẽ. Xét hàm số $g(x) = f\left( 2x^{3} + x - 1 \right) + m$. Với giá trị nào của m thì giá trị nhỏ nhất của $g(x)$trên đoạn $\lbrack 0;1\rbrack$bằng $2021$?

Cho hàm số $y = (x + m)^{3} - 3(x + m) + 1 + n$. Biết hàm số nghịch biến trên khoảng $(0;2)$và giá

trị lớn nhất của hàm số trên $\lbrack - 1;1\rbrack$ bằng $4$. Giá trị $m + n$ bằng

Cho hai hàm số $f(x) = x^{3} + ax^{2} + bx + c$ và $g(x) = x + \dfrac{4}{x^{2}}$. Trên đoạn $\lbrack 1;4\rbrack$, hai hàm số $f(x)$và $g(x)$ có cùng giá trị nhỏ nhất và đạt tại cùng một điểm. Biết rằng điểm $A(1;4)$ thuộc đồ thị của hàm số $f(x)$. Giá trị lớn nhất của hàm số $f(x)$ trên đoạn $\lbrack 1;4\rbrack$ là

Cho hàm số $y = f(x) = 2x^{2} - 4x - 2.$ Gọi $S$ là tổng tất cả các giá trị của tham số $m$ để hàm số $y = g(x) = \left| f^{2}(x) - 2f(x) + m \right|$ đạt giá trị lớn nhất trên đoạn $\lbrack - 1;3\rbrack$ bằng $15.$ Tổng $S$ thuộc khoảng nào sau đây?

Cho hàm số $f(x) = \left| 2x^{2} + (a + 4)x + b + 3 \right|$. Đặt $M = \max_{\lbrack - 2;3\rbrack}f(x)$. Khi $M$ đạt giá trị nhỏ nhất, giá trị của biểu thức $T = a + 4b$ là

Cho bất phương trình $m\left(\sqrt{x^{2}-2 x+2}+1\right)+x(2-x) \leq 0$.

Hỏi có bao nhiêu số nguyên $m$ không nhỏ hơn $-2022$ đề bất phương trình đã cho có nghiệm $x \in[0 ; 1+\sqrt{3}]$ ?