Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Góc tạo bởi tiếp tuyến và dây cung SVIP
Cho nửa đường tròn $(O)$ đường kính $AB$. Trên tia đối của tia $AB$ lấy một điểm $M$. Vẽ tiếp tuyến $MC$ với nửa đường tròn. Gọi $H$ là hình chiếu của $C$ trên $AB$.
a) Chứng minh rằng $CA$ là tia phân giác của góc $MCH$.
b) Giả sử $MA = a$, $MC = 2a$. Tính \(AB\) và $CH$ theo $a$.
Hướng dẫn giải:

a) Ta có \(\widehat{ACH}=\widehat{ABC}\) (cùng phụ với góc CAH).
Mà \(\widehat{ABC}=\widehat{MCA}\) (Cùng chắn cung AC)
Vậy \(\widehat{MCA}=\widehat{ACH}\) hay CA là tia phân giác góc MCH.
b) Vì MC là tiếp tuyến, MAB là cát tuyến cùng xuất phát từ điểm M nên MA.MB = MC2.
\(\Rightarrow MB=\dfrac{MC^2}{MA}=\dfrac{4a^2}{a}=4a\)
\(AB=MB-MA=4a-a=3a\), do đó \(OC=\dfrac{3a}{2}\) (O là tâm đường tròn đường kính AB = 3a).
\(OM=OA+MA=\dfrac{3a}{2}+a=\dfrac{5a}{2}\)
Trong tam giác vuông OMC, đường cao CH ta có:
\(OH.OM=OC^2\) nên \(OH=\dfrac{OC^2}{OM}=\left(\dfrac{3a}{2}\right)^2:\left(\dfrac{5a}{2}\right)=\dfrac{9a}{10}\)
\(CH^2=OC^2-OH^2=\left(\dfrac{3a}{2}\right)^2:\left(\dfrac{9a}{10}\right)^2=\dfrac{144a^2}{100}\)
\(\Rightarrow CH=\dfrac{12a}{10}=\dfrac{6a}{5}.\)
Cho hai đường tròn tâm \(O_1,O_2\) tiếp xúc ngoài nhau tại $A$. Trên đường tròn \(\left(O_1\right)\) lấy hai điểm $B$, $C$ phân biệt khác $A$. Các đường thẳng $BA$, $CA$ cắt đường tròn \(\left(O_2\right)\) tại $P$ và $Q$. Chứng minh $PQ$//$BC$.
Hướng dẫn giải:
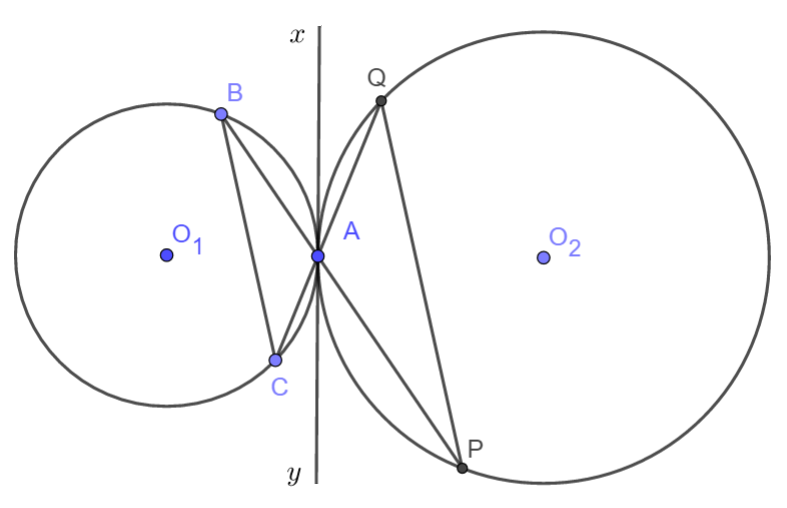
Kẻ tiếp tuyến chung tại $A$ của hai đường tròn \(\left(O_1\right),\left(O_2\right)\).
Có \(\widehat{xAC}=\widehat{QAy}\) (hai góc đối đỉnh).
Theo tính chất của góc tạo bởi tiếp tuyến và dây cung:
\(\widehat{CAx}=\dfrac{1}{2}sđ\stackrel\frown{CA}\); \(\widehat{yAQ}=\dfrac{1}{2}sđ\stackrel\frown{AQ}.\)
Theo tính chất của góc nội tiếp ta có:
\(\widehat{CBA}=\dfrac{1}{2}sđ\stackrel\frown{CA}\); \(\widehat{APQ}=\dfrac{1}{2}sđ\stackrel\frown{AQ}.\)
Vì vậy \(\widehat{CBA}=\widehat{APQ}\).
Suy ra: $PQ$//$BC$.
Cho đường tròn \(\left(O_1\right)\) tiếp xúc trong với đường tròn $(O)$ tại $A$. Đường kính $AB$ của đường tròn $(O)$ cắt đường tròn \(\left(O_1\right)\) tại điểm thứ hai $C$ khác $A$. Từ $B$ vẽ tiếp tuyến $BP$ với đường tròn \(\left(O_1\right)\) cắt đường tròn \(\left(O\right)\) tại $Q$. Chứng minh $AP$ là tia phân giác của góc \(\widehat{QAB}\).
Hướng dẫn giải:
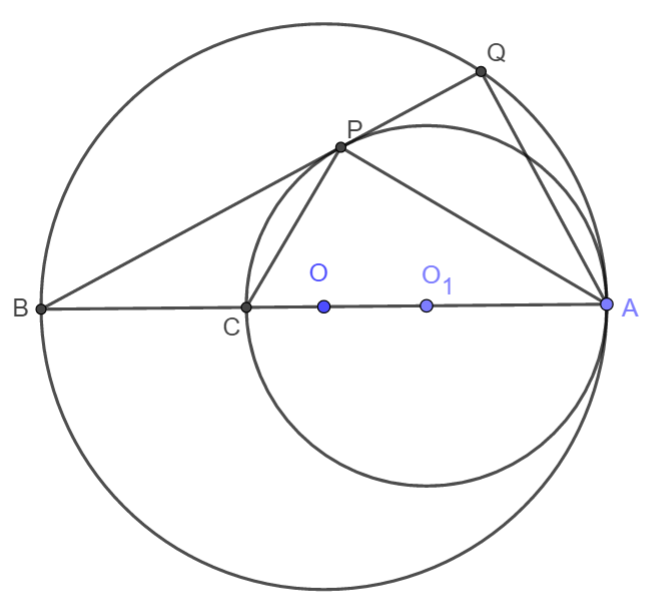
Có \(\widehat{AQP}=90^o\) (góc nội tiếp chắn nửa đường tròn).
Suy ra:
\(\widehat{QAP}=90^o-\widehat{QPA}=90^o-\dfrac{1}{2}sđ\stackrel\frown{AP}.\)
Có \(\widehat{APC}=90^o\) (góc nội tiếp chắn nửa đường tròn).
Suy ra:
\(\widehat{PAC}=90^o-\widehat{PCA}=90^o-\dfrac{1}{2}sđ\stackrel\frown{AP}.\)
Vì vậy \(\widehat{QAP}=\widehat{PAC}\). Suy ra AP là tia phân giác của góc \(\widehat{QAB}\).
Cho nửa đường tròn $(O)$ đường kính $AB = 2R$, dây $AC$ và tia tiếp tuyến $Bx$ nằm trên cùng nửa mặt phẳng bờ $AB$ chứa nửa đường tròn. Tia phân giác của góc $CAB$ cắt dây $BC$ tại $F$, cắt nửa đường tròn tại $H$, cắt $Bx$ ở $D$.
a) Chứng minh $FB = DB$ và $HF = HD$.
b) Gọi $M$ là giao điểm của $AC$ và $Bx$. Chứng minh $AC.AM = AH.AD$.
c) Tính tích $AF.AH + BF.BC$ theo bán kính $R$ của đường tròn $(O)$.
Hướng dẫn giải:
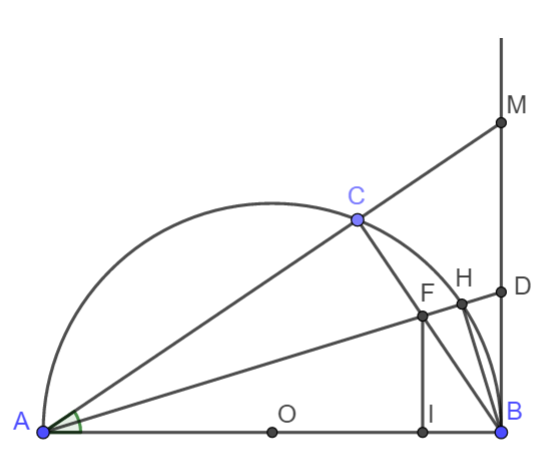
a) Do AD là tia phân giác của \(\widehat{CAB}\) nên \(sđ\stackrel\frown{CH}=sđ\stackrel\frown{HB}.\)
\(\widehat{CBH}=\dfrac{1}{2}sđ\stackrel\frown{CH}\); \(\widehat{HBD}=\dfrac{1}{2}sđ\stackrel\frown{HB}.\)
Suy ra: \(\widehat{CBH}=\widehat{HBD}\) hay BH là tia phân giác của \(\widehat{FBD}\).
Có \(\widehat{AHB}=90^o\) (góc nội tiếp chắn nửa đường tròn) nên \(BH\perp AD\).
Tam giác HBF và tam giác HBD có BH vừa là đường cao, vừa là đường phân giác nên BFD là tam giác cân tại B.
Vậy FB = DB và HF = HD.
b) Theo hệ thức lượng trong tam giác vuông:
\(AC.AM=AB^2\) và \(AH.AD=AB^2\).
Suy ra: \(AC.AM=AH.AD\).
c) Kẻ \(FI\perp AB\left(I\in AB\right)\).
Tứ giác ACFI và BIFH nội tiếp nên BF.BC = BI.BA và AF.AH = AI.AB.
Do đó BF.BC + AF.AH = (BI + AI).BA = BA2 = 4R2.
Cho tam giác $ABC$ vuông ở $A$ nội tiếp đường tròn tâm $O$ đường kính $5cm$. Tiếp tuyến với đường tròn tại $C$ cắt tia phân giác của góc $ABC$ tại $K$. $BK$ cắt $AC$ tại $D$ và $BD = 4cm$. Tính độ dài $BK$.
Hướng dẫn giải:
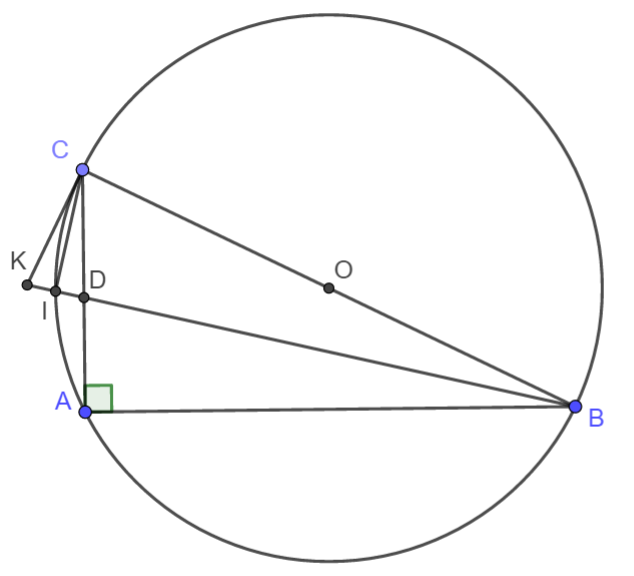
Gọi I là giao điểm của BD và đường tròn (O). Do BI là tia phân giác của \(\widehat{ABC}\) nên I là điểm chính giữa cung AC.
Vì vậy \(sđ\stackrel\frown{AI}=sđ\stackrel\frown{IC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\). (1)
Theo tính chất góc tạo bởi tiếp tuyến và dây cung \(\widehat{ICK}=\dfrac{1}{2}sđ\stackrel\frown{CI}\). (2)
Theo tính chất của góc nội tiếp \(\widehat{ACI}=\dfrac{1}{2}sđ\stackrel\frown{AI}\). (3)
Từ (1), (2), (3) suy ra CI là tia phân giác của góc DCK.
Mà \(\widehat{CIB}=90^o\) nên \(CI\perp BK\).
Tam giác DCK có CI vừa là đường cao vừa là đường phân giác nên là tam giác cân. Vậy CI đồng thời là trung tuyến, hay DI = IK.
Đặt $DI = IK = x$.
\(BI=BD+DI=4+x,BK=BD+DK=4+2x\).
Vì BI là hình chiếu vuông góc từ C xuống cạnh huyền BK nên
\(BI.BK=BC^2\)
Suy ra: \(\left(4+x\right)\left(4+2x\right)=5\)
\(\Leftrightarrow2x^2+12x-9=0\)
\(\Leftrightarrow x=\dfrac{-6+3\sqrt{6}}{2}\).
\(BK=BD+2x=4+2.\dfrac{-6+3\sqrt{6}}{2}=-2+3\sqrt{6}\).
Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Kẻ các tiếp tuyến AB, AC và cát tuyến ADE với đường tròn (D nằm giữa A và E). Tia phân giác của góc DBE cắt DE tại I. Chứng minh rằng:
a) $\dfrac{BD}{BE}=\dfrac{CD}{CE}$;
b) $AI = AB = AC$;
c) $CI$ là tia phân giác của góc $DCE$.
Hướng dẫn giải:
b) Chứng minh tam giác $ABI$ cân tại $A$.
c) Ngược lại với câu b, chú ý rằng tam giác $ACI$ cân tại $A$, \(\widehat{ACD}=\widehat{DEC}\).
Cho hai đường tròn (O ; R) và (O’ ; r), (R > r) tiếp xúc trong tại A. Dây BC của (O ; R) tiếp xúc với (O’ ; r) tại M (ba điểm A, O, M không thẳng hàng). Chứng minh tia AM là tia phân giác của góc BAC.
Hướng dẫn giải:
Do (O) và (O’) tiếp xúc với nhau nên tiếp điểm A nằm trên đường thẳng OO’.
Gọi N là giao điểm của AM và (O).
Chứng minh được O’M // ON.
Từ đó chứng minh được N là điểm chính giữa cung BC của đường tròn (O).
Cho hai đường tròn (O) và (O’) ở ngoài nhau. Đường nối tâm OO’ cắt các đường tròn (O) và (O’) tại các điểm A, B, C, D theo thứ tự đó trên đường thẳng. Kẻ tiếp tuyến chung ngoài EF, E ∈ (O), F ∈ (O’). Gọi M là giao điểm của AE và DF, N là giao điểm của EB và FC. Chứng minh rằng:
a) MENF là hình chữ nhật.
b) MN vuông góc với AD.
c) ME.NA = MF.MD.
Hướng dẫn giải:
a) Chứng minh tứ giác MENF có ba góc vuông.
Chứng minh được \(\widehat{FEN}+\widehat{EFN}=90^\circ.\)
b) Chứng minh \(\widehat{M_1}+\widehat{A}=90^\circ.\)
Từ điểm A ở bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn. Gọi BD là dây của đường tròn song song với AC, E là giao điểm của AD với đường tròn, I là giao điểm của BE và AC. Chứng minh rằng I là trung điểm của AC.
Hướng dẫn giải:
Chứng minh \(AI^2=IC^2\) (cùng bằng $BI . EI$).




