Bài học cùng chủ đề
- Định lý côsin
- Định lí sin
- Một số công thức tính diện tích tam giác
- Định lí côsin, định lí sin và ứng dụng
- Tính bán kính đường tròn ngoại tiếp và nội tiếp trong tam giác qua diện tích
- Diện tích tam giác
- Bài tập tự luận (nâng cao)
- Phiếu bài tập: Định lí sin - côsin
- Phiếu bài tập: Diện tích tam giác
- Định lí côsin và định lí sin
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Định lí côsin và định lí sin SVIP
Nội dung này do giáo viên tự biên soạn.
1. ĐỊNH LÍ CÔSIN TRONG TAM GIÁC
Định lí côsin
Trong tam giác \(ABC\) với \(BC=a,CA=b,AB=c.\) Khi đó:
\(a^{^{ }2}=b^2+c^2-2bc\cos A,\)
\(b^{^{ }2}=c^2+a^2-2ca\cos B,\)
\(c^{^{ }2}=a^2+b^2-2ab\cos C\).
Hệ quả:
\(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\);
\(\cos B=\dfrac{c^2+a^2-b^2}{2ca}\);
\(\cos C=\dfrac{a^2+b^2-c^2}{2ab}\).
Ví dụ. Cho tam giác \(ABC\) có các cạnh \(AC=10\) cm, \(BC=16\) cm và góc \(C\) bằng \(110^\circ\). Tính cạnh \(AB\) và góc \(A\) của tam giác đó.
Giải
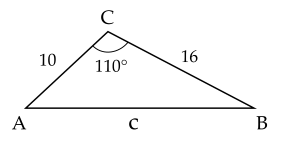
Theo định lí côsin ta có:
\(AB^2=CA^2+CB^2-2CA.CB.\cos\widehat{C}\)
\(AB^2=16^2+10^2-2.16.10\)\(\cos110^\circ\)
\(AB^2\approx465,44\)
suy ra \(AB\approx\sqrt{465,44}\approx21,6\) (cm).
Theo hệ quả định lí côsin, ta có:
\(\cos A=\dfrac{AB^2+AC^2-BC^2}{2.AB.AC}\)
\(\cos A\approx\dfrac{10^2+\left(21,6\right)^2-16^2}{2.10.21,6}\approx0,72\)
suy ra \(A\approx\) \(43^\circ56'\).
2. ĐỊNH LÍ SIN TRONG TAM GIÁC
Định lí sin
Trong tam giác \(ABC\) có \(BC=a,CA=b,AB=c\) và bán kính đường tròn ngoại tiếp bằng \(R\). Khi đó:
\(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\).
Hệ quả
\(a=2R\sin A;\) \(b=2R\sin B;\) \(c=2R\sin C;\)
\(\sin A=\dfrac{a}{2R};\) \(\sin B=\dfrac{b}{2R};\) \(\sin C=\dfrac{c}{2R}.\)
Ví dụ. Cho tam giác \(ABC\) có \(AB=6\) cm, \(\widehat{B}=30^\circ,\widehat{C}=45^\circ\), tính độ dài cạnh \(AC\) và bán kính đường tròn ngoại tiếp tam giác \(ABC.\)
Giải
Áp dụng định lí sin trong tam giác \(ABC\) ta có:
\(\dfrac{AC}{\sin B}=\dfrac{AB}{\sin C}\Rightarrow AC=\dfrac{AB.\sin B}{\sin C}=\dfrac{6.\sin30^\circ}{\sin45^\circ}\approx4,24\) cm.
Ta lại có
\(\dfrac{AB}{\sin C}=2R\Rightarrow R=\dfrac{AB}{2.\sin C}=\dfrac{6}{2.\sin45^\circ}\approx4,24\) cm.
3. CÁC CÔNG THỨC TÍNH DIỆN TÍCH TAM GIÁC
Trong tam giác \(ABC\), ta kí hiệu:
- \(A,B,C\) là các góc của tam giác tại các đỉnh tương ứng.
- \(a,b,c\) tương ứng là độ dài của các cạnh đối diện với đỉnh \(A,B,C\).
- \(h_a,h_b,h_c\) là độ dài các đường cao lần lượt tương ứng với các cạnh \(BC,CA,AB.\)
- \(p\) là nửa chu vi.
- \(S\) là diện tích.
- \(R,r\) tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
\(1\)) \(S=\dfrac{1}{2}ah_a=\dfrac{1}{2}bh_b=\dfrac{1}{2}ch_c;\)
\(2\)) \(S=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}ca\sin B=\dfrac{1}{2}ab\sin C;\)
\(3\)) \(S=\dfrac{abc}{4R};\)
\(4\)) \(S=pr;\)
\(5\)) \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) (công thức Heron)

Bạn có thể đánh giá bài học này ở đây