Đề số 2 (Phần tự luận 7 điểm) SVIP

Hướng dẫn giải:

a) $(5x^3y^2 - 3x^2y + xy) \, : \, xy = 5x^2y-3x+1$.

b) Ta có: $A + 2M = P$

$A = P - 2M $

$A = 3x^3- 2x^2y - xy + 3 - 2\left( x^3- x^2y + 2xy + 3 \right) $

$A = 3x^3- 2x^2y - 2xy + 3 - 2x^3+ 2x^2y - 4xy - 6 $

$A = x^3- 6xy - 3$.

Hướng dẫn giải:

a) $2 ( 3x-1) = 10 $

$6x-2=10$

$6x=12$

$x=2$

Vậy $x = 2$

b) $\left( 3x+4 \right)^2-\left( 3x-1 \right)\left( 3x+1 \right)=49$

$9{{x}^{2}}+24x+16-9{{x}^{2}}+1=49$

$24x=32$

$x=\dfrac{4}{3}$

Vậy $x=\dfrac{4}{3}$.​

Hướng dẫn giải:

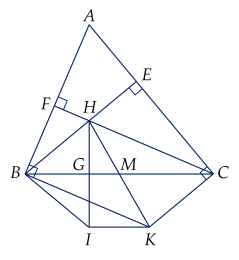
a) Ta có $\left\{ \begin{aligned} & BH\bot AC \\ & KC\bot AC \\ \end{aligned} \right.$ suy ra $BH$ // $KC$ $\left( 1 \right)$

Và $\left\{ \begin{aligned} & CH\bot AB \\ & KB\bot AB \\ \end{aligned} \right.$ suy ra $CH$ // $KB$ $\left( 2 \right)$

Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $BHCK$ là hình bình hành.

b) Vì $BHCK$ là hình bình hành nên $BC$ cắt $HK$ tại trung điểm $M$ của $BC$

$M$ là trung điểm của $HK$ suy ra $H,\,\,M,\,\,K$ thẳng hàng.

c) $\Delta BHI$ có $BG$ vừa là đường cao, trung tuyến nên $BG$ là trung trực của $HI\,.$

Khi đó $MH=MI$

$\Delta HIK$ có $IM$ là đường trung tuyến và $IM=\dfrac{1}{2}HK$ suy ra $\Delta HIK$ vuông tại $I$

Suy ra $IK\bot HI.$

Mà $BC\bot HI$ nên $BC$ // $ IK$ suy ra $BCKI$ là hình thang.

$\Delta BIH$ cân tại $B$ lại có $BG$ là trung trực nên cũng là phân giác của $\widehat{HBI}$

Do đó $\widehat{GBI}=\widehat{GBH}$

Mà $\widehat{HBG}=\widehat{GCK}$ (hai góc so le trong) nên $\widehat{IBC}=\widehat{KCB}$

Suy ra $BCKI$ là hình thang cân.​

Hướng dẫn giải:

a) Số mét khối nước cần có để bơm đầy bể bơi thứ nhất:

     $1,2 x y$ (m$^3$) 

Số mét khối nước cần có để bơm đầy bể bơi thứ hai:

     $1,5. 5 x . 5 y=37,5 x y$ (m$^3$) 

Số mét khối nước cần có để bơm đầy cả hai bể bơi:

     $1,2 x y+37,5 x y=38,7 x y$ (m$^3$).

b) Lượng nước bơm đầy hai bể nếu $x=4$ m, $y=3$ m là:

$38,7.4 . 3=464,4$ (m$^3$)​.