Đề số 2 (Phần tự luận 7 điểm) SVIP

Hướng dẫn giải:

1.

a) Bậc của đa thức $P$ là $3$

Đa thức $P$ có $4$ hạng tử là $2{{x}^{2}}y$; $-3x$; $8{{y}^{2}};$ $-1$

b) Thay $x=-1; \, y=\dfrac{1}{2}$ vào đa thức $P$ ta có:

$P=2.{{(-1)}^{2}}.\dfrac{1}{2}-3.(-1)+8.{{\Big( \dfrac{1}{2} \Big)}^{2}}-1$

$ =2.1.\dfrac{1}{2}+3+8.\dfrac{1}{4}-1 $

$=1+3+2-1 =5$.

Vậy $P=5$ tại $x=-1; \, y=\dfrac{1}{2}$.

2. $P=5x{{y}^{2}}-3{{x}^{2}}+2y-1$ và $Q=-x{{y}^{2}}+9{{x}^{2}}y-2y+6$

$P+Q=(5x{{y}^{2}}-3{{x}^{2}}+2y-1)+(-x{{y}^{2}}+9{{x}^{2}}y-2y+6)$

$=5x{{y}^{2}}-3{{x}^{2}}+2y-1-x{{y}^{2}}+9{{x}^{2}}y-2y+6$

$=(5x{{y}^{2}}-x{{y}^{2}})-3{{x}^{2}}+(2y-2y)+(-1+6)+9{{x}^{2}}y $

$=4x{{y}^{2}}-3{{x}^{2}}+5+9{{x}^{2}}y $.

$P-Q=(5x{{y}^{2}}-3{{x}^{2}}+2y-1)-(-x{{y}^{2}}+9{{x}^{2}}y-2y+6) $

$=5x{{y}^{2}}-3{{x}^{2}}+2y-1+x{{y}^{2}}-9{{x}^{2}}y+2y-6 $

$=(5x{{y}^{2}}+x{{y}^{2}})-3{{x}^{2}}+(2y+2y)+(-1-6)-9{{x}^{2}}y $

$=6x{{y}^{2}}-3{{x}^{2}}+4y-7-9{{x}^{2}}y$.

Hướng dẫn giải:

a) $\left( x-2y \right)\left( 3xy+6{{x}^{2}}+x \right)$

$=3{{x}^{2}}y-6x{{y}^{2}}+6{{x}^{3}}-12{{x}^{2}}y+{{x}^{2}}-2xy$

$=-9{{x}^{2}}y-6x{{y}^{2}}+6{{x}^{3}}+{{x}^{2}}-2xy$

b) $\left( 18{{x}^{4}}{{y}^{3}}-24{{x}^{3}}{{y}^{4}}+12{{x}^{3}}{{y}^{3}} \right) \, : \, \left( -6{{x}^{2}}{{y}^{3}} \right) $

$=-3{{x}^{2}}+4xy-2x$.​

Hướng dẫn giải:

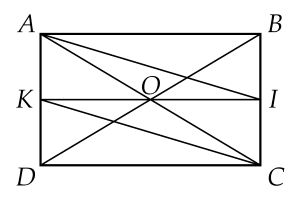
a) ​Tứ giác $ABCD$ là hình chữ nhật (GT)

Suy ra $AD$ // $IC$ (hai cạnh đối) nên tứ giác $AICD$ là hình thang.

Mà $\widehat{ADC}={{90}^{\circ}}$ (góc của hình chữ nhật)

Do đó tứ giác $AICD$ là hình thang vuông.

b) Tứ giác $ABCD$ là hình chữ nhật nên $AD$ // $BC, \, AD = BC$.

Mà $I$, $K$ lần lượt là trung điểm của $BC$, $AD$.

Suy ra $ AK$ // $IC$ và $AK = IC$.

Tứ giác $AICK$ có $AK$ // $IC$ và $AK = IC$ nên tứ giác $AICK$ là hình bình hành (dấu hiệu nhận biết).

c) Gọi $O$ là giao điểm của $AC$ và $BD$

Suy ra $O$ là trung điểm của $AC$ và $BD$ (1) (tính chất đường chéo hình chữ nhật)

Tứ giác $AICK$ là hình bình hành (chứng minh trên).

Suy ra $AC$ cắt $IK$ tại trung điểm của $AC $ (2)

Từ (1) và (2) suy ra $O$ là trung điểm của $AC$, $IK$ và $BD$.

Hay ba đường thẳng $AC$, $BD$, $IK$ cùng đi qua điểm $O$.

Hướng dẫn giải:

a) Ta có $h=20 t-16 t^2 = 4t(5 - 4t)$.

b) Với $t = 0,5 $ thì $4t = 2$ vào biểu thức trên ta được:

$h = 2(5 - 2) = 6$ (ft) $= 6.30,48 = 183$ (cm).