Đề KSCL học kỳ 2 năm 2022 sở GD&ĐT Nam Định SVIP

Hướng dẫn giải:

1. $\left(1-\dfrac{5+\sqrt{2}}{\sqrt{2}+1}\right) \cdot \sqrt{3+2 \sqrt{2}}=\dfrac{-4}{\sqrt{2}+1} \sqrt{(\sqrt{2}+1)^{2}}=-4$.

2. Với $x>0 ; x \neq 1$ ta có:
$A=\left(\dfrac{\sqrt{x}}{x+\sqrt{x}}-\dfrac{1}{\sqrt{x}-1}\right): \dfrac{2}{x+\sqrt{x}-2}$
$\Leftrightarrow A=\left(\dfrac{\sqrt{x}}{\sqrt{x}(\sqrt{x}+1)}-\dfrac{1}{\sqrt{x}-1}\right): \dfrac{2}{(\sqrt{x}-1)(\sqrt{x}+2)}$
$\Leftrightarrow A=\dfrac{-2}{(\sqrt{x}-1)(\sqrt{x}+1)} \cdot \dfrac{(\sqrt{x}-1)(\sqrt{x}+2)}{2}$
$\Leftrightarrow A=\dfrac{-(\sqrt{x}+2)}{\sqrt{x}+1}$. Vạyy với $x>0 ; x \neq 1$, ta có $A=\dfrac{-(\sqrt{x}+2)}{\sqrt{x}+1}$.

Hướng dẫn giải:

1) Tung độ của $A$ bằng 5 nên ta có: $5=\frac{1}{5} x^{2} \Leftrightarrow x^{2}=25 \Leftrightarrow x=\pm 5$.
Toạ độ điềm $A$ là: $A(-5 ; 5)$ hoặc $A(5 ; 5)$.

2) Ta có $\Delta^{\prime}=(m+3)^{2}-m^{2}=6 m+9$
Phương trình có hai nghiệm phân biệt $x_{1}, x_{2} \Leftrightarrow \Delta^{\prime}>0 \Leftrightarrow m>-\frac{3}{2}$.
Với đk (1) ta có hệ thức Viet: $\left\{\begin{array}{l}x_{1}+x_{2}=2(m +3) \\ x_{1} x_{2}=m^{2}\end{array}\right.$
$x_{1}{ }^{2}+x_{2}{ }^{2}+x_{1} x_{2}=15 \Leftrightarrow\left(x_{1}+x_{2}\right)^{2}-x_{1} x_{2}=15$. Thay hệ thức Viet ta được:
$4(m+3)^{2}-m^{2}=15 \Leftrightarrow m^{2}+8 m+7=0 \Leftrightarrow\left[\begin{array}{l}m=-1 \\ m=-7\end{array}\right.$
Đối chiếu đk (1), vậy giá trị cần tìm là $m=-1$.

Hướng dẫn giải:

Đặt $\frac{1}{x-1}=a, \frac{1}{y}=b .$ Ta có hệ:

\(\left\{{}\begin{matrix}3a+4b=13\\2a-5b=1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=1\end{matrix}\right.\)

Ta có : $\frac{1}{x-1}=3\Leftrightarrow x=\frac{4}{3};\frac{1}{y}=1 \Leftrightarrow y=1$.
Vậy hệ phương trình đã cho có 1 nghiệm $(x ; y)=\left(\frac{4}{3};1\right)$.

Hướng dẫn giải:

Diện tích hình vuông $A B C D$ là $S_{1}=A B^{2}=36\left(\mathrm{~cm}^{2}\right)$.
Diện tích nửa hình tròn tâm $O$ đường kính $A D$ là $S_{2}=\frac{9 \pi}{2}\left(\mathrm{~cm}^{2}\right)$.
Tinh được $H E=3 \mathrm{~cm}$.
Diện tích hình tròn tâm $I$ đường kính $H E$ là $S_{3}=\frac{9 \pi}{4}\left(\mathrm{~cm}^{2}\right)$.
Diện tích phần hình tô đậm là $S=S_{1}-\left(S_{2}+S_{3}\right) \simeq 14,8\left(\mathrm{~cm}^{2}\right)$.

Hướng dẫn giải:

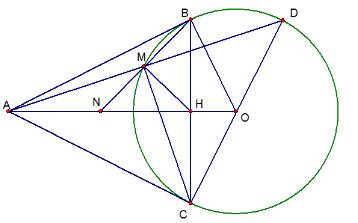
a) Vì $A B, A C$ là các tiếp tuyến với đường tròn $(O)(B, C$ là các tiếp điểm ) nên $A B=A C$ và $O B=O C$. Do đó $A O$ là đường trung trực của $B C$.
Suy ra $A O \perp B C$ hay $\widehat{ A H C}=90^{\circ}$
Vi $C D$ là đường kính của $(O)$ nên $\widehat{ D M C}=90^{\circ} \Rightarrow \widehat{ A M C}=90^{\circ}$.
Tứ giác $A M H C$ có $\widehat{ A M C}=\widehat{ A H C}=90^{\circ}$
Vậy tứ giác $A M H C$ nội tiếp.

b) Vì tứ giác $A M H C$ nội tiếp nên $\angle M A H=\angle M C H$
Trong $(O)$ có $\widehat{ABM}=\widehat{M C H}$ ( góc tạo bời tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung ) 
$\widehat{ M A H}=\widehat{ A B M}(=\widehat{ M C H})$ hay $\widehat{ M A N}=\widehat{ A B N}$.
Xét $\triangle N A M$ và $\triangle N B A$ có $\widehat{ M A N}=\widehat{ A B N}$ và $\widehat{ M N A}$ chung nên $\triangle N A M \backsim \triangle N B A \Rightarrow \frac{N A}{N B}=\frac{N M}{N A} \Rightarrow N A^{2}=N M \cdot N B\ (1)$
Vì tứ giác $AHMC$ nội tiếp nên $\angle M H A=\angle M C A$
Có $\widehat{ M B C}=\widehat{ M C A}$ (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung ) $\widehat{ M B H}=\widehat{ A H M}(=\widehat{ M C A})$ hay
$\widehat{ M H N}=\widehat{ H B N}$
Xét $\triangle N H M$ và $\triangle N B H$ có $\widehat{ M H N}=\widehat{ H B N}$ và $\widehat{ M N H}$ chung nên $\triangle N H M\backsim\triangle N B H$
$\Rightarrow \frac{N H}{N B}=\frac{N M}{N H} \Rightarrow N H^{2}=N M \cdot N B\ (2)$
Từ (1) và (2) suy ra $N A^{2}=N H^{2} \Rightarrow N A=N H$
Vậy $N$ là trung điểm của $A H$.

Hướng dẫn giải:

Điều kiện $-3 \leq x \leq \frac{3}{2}$.
Phương trình $\Leftrightarrow 11-x-4 \sqrt{x+3}-2 \sqrt{3-2 x}=0$ $\Leftrightarrow x+3-4 \sqrt{x+3}+4+3-2 x-2 \sqrt{3-2 x}+1=0$

\(\begin{aligned} &\Leftrightarrow(\sqrt{x+3}-2)^{2}+(\sqrt{3-2 x}-1)^{2}=0 \\ &\Leftrightarrow\left\{\begin{array}{l} &\sqrt{x+3}=2 \\ &\sqrt{3-2 x}=1 \end{array} \Leftrightarrow x=1(\text{TMĐK})\right. \end{aligned}\)
Vậy nghiệm phương trình đã cho là $x=1$.

Hướng dẫn giải:

Trước hết chứng minh: Với hai số dương $x, y$ ta có : $\dfrac{1}{x}+\dfrac{1}{y} \geq \dfrac{4}{x+y}\left(^{*}\right)$.

Áp dụng (*) ta có $\dfrac{1}{x y}=\dfrac{x+y}{x y}=\dfrac{1}{x}+\dfrac{1}{y} \geq \dfrac{4}{x+y}=4$.
Ta có:

\(\begin{aligned} A &=\dfrac{2}{x y}+\dfrac{3}{x^{2}+y^{2}}=\dfrac{1}{2 x y}+3\left(\dfrac{1}{2 x y}+\dfrac{1}{x^{2}+y^{2}}\right) \\ & \geq \dfrac{1}{2 x y}+3 \cdot \dfrac{4}{x^{2}+2 x y+y^{2}}=\dfrac{1}{2} \cdot \dfrac{1}{x y}+12 \geq 2+12=14 . \end{aligned}\)
Dấu "=" xảy ra khi $\left\{\begin{array}{l}x=y \\ x+y=1\end{array} \Leftrightarrow x=y=\dfrac{1}{2}\right.$.
Vậy giá trị nhỏ nhất của $A=14$ khi $x=y=\dfrac{1}{2}$.