Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 2) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Mệnh đề phủ định của "20 là số hợp số" là
Cho tập hợp B gồm các số nguyên tố có một chữ số. Tập hợp B viết bằng cách liệt kê các phần tử của tập hợp là
Bất phương trình nào sau đây không là bất phương trình bậc nhất hai ẩn?
Miền nghiệm của bất phương trình 5(x+2)−9<2x−2y+7 là phần mặt phẳng không chứa điểm nào sau đây?
Parabol y=x2−4x+3 có tọa độ đỉnh là
Giá trị của biểu thức A=sin215∘+sin275∘+cos120∘ là
Cho tam giác ABC có AB=3, BC=5 và độ dài đường trung tuyến BM=13.
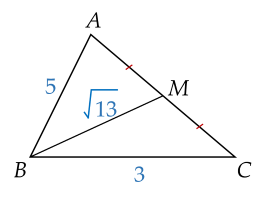
Độ dài AC bằng
Cho tam giác ABC có góc B=60∘, C=45∘, cạnh AB=4. Độ dài cạnh AC bằng
Mệnh đề phủ định của "Hà Nội là thủ đô của nước Việt Nam" là
Cho tập hợp A=(−∞;m−1), B=(2;+∞). Giá trị của m để A∩B=∅ là
Phần tô màu (không bao gồm đường thẳng d) trong hình vẽ là miền nghiệm của bất phương trình nào sau đây?
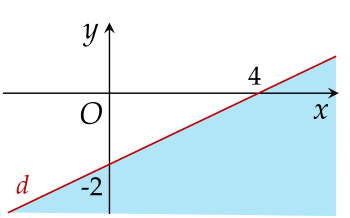
Phần không tô màu là hình vẽ biểu diễn miền nghiệm của hệ bất phương trình nào dưới đây?
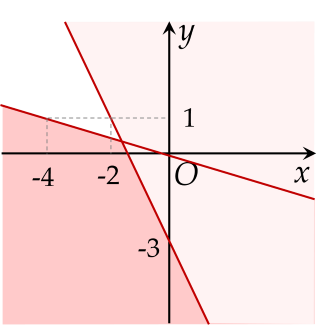
Cho ba tập hợp CRM=(−∞;3),CRN=(−∞;−3)∪(3;+∞) và CRP=(−2;3].
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) N=(−3;3). |
|
| b) P=(−∞;−2]∪(3;+∞). |
|
| c) M∩N=∅. |
|
| d) (M∩N)∪P=(−∞;−2]∪[3;+∞). |
|
Cho A là tập hợp các học sinh lớp 10 đang học ở trường X và B là tập hợp các học sinh đang học môn Tiếng Anh của trường X.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) A∩B là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường X. |
|
| b) A\B là tập hợp những học sinh lớp 10 và không học Tiếng Anh ở trường X. |
|
| c) A∪B là tập hợp các học sinh lớp 10 và học sinh học môn Tiếng Anh ở trường X. |
|
| d) B\A là tập hợp các học sinh học lớp 10 ở trường X nhưng không học môn Tiếng Anh. |
|
Bà Lan được tư vấn bổ sung chế độ ăn kiêng đặc biệt bằng cách sử dụng hai loại thực phẩm khác nhau là X và Y. Mỗi gói thực phẩm X chứa 20 đơn vị canxi, 20 đơn vị sắt và 10 đơn vị vitamin B. Mỗi gói thực phẩm Y chứa 20 đơn vị canxi, 10 đơn vị sắt và 20 đơn vị vitamin B. Yêu cầu hằng ngày tối thiểu trong chế độ ăn uống là 240 đơn vị canxi, 160 đơn vị sắt và 140 đơn vị vitamin B. Mỗi ngày không được dùng quá 12 gói mỗi loại.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hệ bất phương mô tả số gói thực phẩm X và thực phẩm Y mà bà Lan cần dùng mỗi ngày trong chế độ ăn kiêng để đáp ứng đủ nhu cầu cần thiết đối với canxi, sắt và vitamin B là ⎩⎨⎧x+y≥122x+y≥16x+2y≥140≤x≤120≤y≤12. |
|
| b) Điểm (10;8) không thuộc miền nghiệm của hệ bất phương trình mô tả số gói thực phẩm X và thực phẩm Y mà bà Lan cần dùng mỗi ngày trong chế độ ăn kiêng để đáp ứng đủ nhu cầu cần thiết đối với canxi, sắt và vitamin B. |
|
| c) Miền nghiệm của hệ bất phương mô tả số gói thực phẩm X và thực phẩm Y mà bà Lan cần dùng mỗi ngày trong chế độ ăn kiêng để đáp ứng đủ nhu cầu cần thiết đối với canxi, sắt và vitamin B là một ngũ giác. |
|
| d) Biết 1 gói thực phẩm loại X giá 20000 đồng, 1 gói thực phẩm loại Y giá 25 000 đồng. Bà Lan cần dùng 10 gói thực phẩm loại X và 2 gói thực phẩm loại Y để chi phí mua là ít nhất. |
|
Cho sinα=31.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) cos2α=98. |
|
| b) A=sin2α+3cos2α=935. |
|
| c) B=5sin2α−cos2α=−31. |
|
| d) C=sin2α+3cos2α+cos2α−7sin2α=2. |
|
Lớp 10A có 21 em thích học Toán, 19 em thích học Văn và có 18 em thích học tiếng Anh. Trong số đó có 9 em thích học cả Toán lẫn Văn, 7 em thích học cả Văn lẫn tiếng Anh, 6 em thích học cả Toán lẫn tiếng Anh và có 4 em thích học cả ba môn Toán, Văn, Anh, không có em nào không thích một trong ba môn học trên. Trong lớp 10A có bao nhiêu học sinh?
Trả lời:
Để chuẩn bị cho đại hội chi đoàn 10A1, bạn Nga được phân công đi mua hoa để cắm vào 3 lọ, mỗi lọ cắm số hoa mỗi loại như nhau. Bạn Nga được lớp giao cho 200 nghìn đồng để mua nhưng đến quầy bán chỉ còn 2 loại hoa và đã mua đủ để cắm. Biết rằng một loại hoa có giá 15 nghìn đồng/bông và một loại có giá 20 nghìn/bông. Số tiền dư ra ít nhất có thể là bao nhiêu nghìn đồng?
Trả lời:
Nhân dịp tết Trung thu, xí nghiệp sản xuất bánh muốn sản xuất hai loại bánh: bánh nướng và bánh dẻo. Để sản xuất hai loại bánh này, xí nghiệp cần: đường, bột mì, trứng, mứt bí, lạp xưởng,. Xí nghiệp đã nhập về 600 kg bột mì và 240 kg đường, các nguyên liệu khác luôn đáp ứng được số lượng mà xí nghiệp cần. Mỗi chiếc bánh nướng cần 120 g bột mì, 60 g đường. Mỗi chiếc bánh dẻo cần 160 g bột mì và 40 g đường. Theo khảo sát thị trường, lượng bánh dẻo tiêu thụ không vượt quá ba lần lượng bánh nướng và sản phẩm của xí nghiệp sản xuất luôn được tiêu thụ hết. Mỗi chiếc bánh nướng lãi 8000 đồng, mỗi chiếc bánh dẻo lãi 6000 đồng, Theo kế hoạch sản xuất, xí nghiệp sẽ sản xuất x chiếc bánh nướng và y chiếc bánh dẻo để đáp ứng nhu cầu thị trường; đảm bảo lượng bột mì, đường không vượt quá số lượng mà xí nghiệp đã chuẩn bị và vẫn thu được lợi nhuận cao nhất. Tính x+y.
Trả lời: .
Cho x,y thoả mãn hệ ⎩⎨⎧x+2y−100≤02x+y−80≤0x≥0y≥0. Khi biểu thức P=(x;y)=40000x+30000y đạt giá trị lớn nhất, tính x+y.
Trả lời:
Trên nóc một tòa nhà có một cột ăngten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50∘ và 40∘ so với phương nằm ngang.
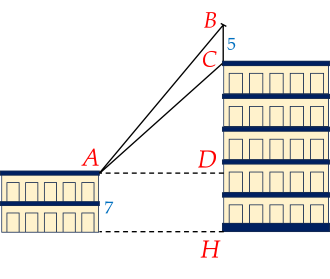
Tính chiều cao của tòa nhà. (Làm tròn kết quả đến chữ số thập phân thứ nhất của đơn vị mét)
Trả lời:
Cho tanα=1. Tính B=2cos2α−sin2αsin2α+1.
Trả lời:
