Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề thi thử học kì I lớp 8 (đề số 3) SVIP
Câu 1. (2 điểm): Phân tích các đa thức sau thành nhân tử:
a) $5 x^3-45 x$;
b) ${x}^2-7 {x}+12$.
Hướng dẫn giải:
a) $5 x^3-45 x=5 x\left(x^2-9\right)=5 x(x-3)(x+3)$;
b) $x^2-7 x+12=x^2-3 x-4 x+12$
$=\left(x^2-3 x\right)-(4 x-12) =x(x-3)-4(x-3)=(x-3)(x-4) $.
Câu 2. (1,5 điểm): Thực hiện các phép tính sau:
a) $(x+2)^2+x(2 x-5)$;
b) $\dfrac{x}{x+3}+\dfrac{2 x}{x-3}+\dfrac{-3 x^2-9}{x^2-9}$ với $x \neq \pm 3$.
Hướng dẫn giải:
a) $(x+2)^2+x(2 x-5)$
$= x^2+4 x+4+2 x^2-5 x$
$= 3 x^2-x+4$.
b) $\dfrac{x}{x+3}+\dfrac{2 x}{x-3}+\dfrac{-3 x^2-9}{x^2-9}$
$=\dfrac{x(x-3)}{(x+3)(x-3)}+\dfrac{2 x(x+3)}{(x+3)(x-3)}+\dfrac{-3 x^2-9}{(x+3)(x-3}$
$=\dfrac{x^2-3 x}{(x+3)(x-3)}+\dfrac{2 x^2+6 x}{(x+3)(x-3)}+\dfrac{-3 x^2-9}{(x+3)(x-3)}$
$=\dfrac{3 x-9}{(x+3)(x-3)}=\dfrac{3}{x+3}$.
Câu 3. (1,5 điểm): Tìm $x$ biết:
a) $(x-1)^2+x(4-x)=11$;
b) $x^2-9-2(x+3)=0$.
Hướng dẫn giải:
a) $(x-1)^2+x(4-x)=11$
$x^2-2 x+1+4 x-x^2=11$
$2 x=10$
$x=5$
b) $x^2-9-2(x+3)=0$
$(x-3)(x+3)-2(x+3)=0$
$(x+3)(x-5)=0$
$x+3=0$ hoặc $x-5=0$
$x=-3$ hoặc $x=5$.
Câu 4. (1,0 điểm):
Bạn Nam và mẹ đến một cửa hàng để tìm mua laptop và thấy giá niêm yết của laptop đó là $13 \, 500 \, 000$ đồng. Do cửa hàng có đợt khuyến mãi nên có thông báo lần đầu giảm giá $10 \%$, sau đó lại giảm thêm $5 \%$ trên giá đã giảm. Vậy sau hai đợt giảm giá thì giá của laptop bạn Nam và mẹ muốn mua là bao nhiêu?
Hướng dẫn giải:
Số tiền mua laptop sau khi giảm lần 1 là:
$13 \, 500 \, 000.90 \%=12 \, 150 \, 000$ (đồng);
Số tiền mua latop sau khi giảm lần 2 là:
$12 \, 150 \, 000.95 \%=11 \, 542 \, 500$ (đồng);
Sau hai đợt giảm giá thì giá của laptop bạn Nam và mẹ muốn mua là: $11$ $542$ $500$ (đồng).
Câu 5. (1 điểm):
Một người thợ làm bánh thiết kế một chiếc bánh cưới có ba tầng hình tròn như hình vẽ.
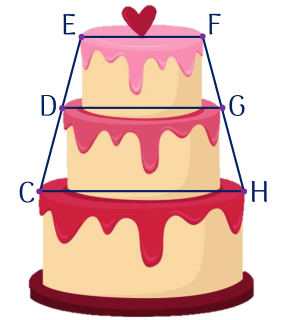
Tầng đáy có đường kính $CH$ là $30$ cm. Tầng thứ 1 có đường kính $EF$ là $10$ cm. Em hãy tính độ dài đường kính $D G$ của tầng 2, nếu biết rằng $EF$ // $CH$ và ${D}$, ${G}$ lần lượt là trung điểm của ${EC}$ và ${FH}$?
Hướng dẫn giải:
Xét hình thang $EFHC$ ($EF$ // $CH$); $D$, $G$ lần lượt là trung điểm của $EC$ và $FH$
Nên $DG$ là đường trung bình của hình thang ${EFHC}$.
Suy ra $D G=\dfrac{E F+H C}{2}=20$ (cm).
Độ dài đường kính ${DG}$ của tầng 2 là $20$ cm.
Câu 6. (3 điểm):
Cho $\Delta ABC$ cân tại $A$. Gọi $E$, $F$, $H$ lần lượt là trung điểm các cạnh $AB$, $AC$, $BC$.
a) Chứng minh $EFCB$ là hình thang cân;
b) Chứng minh $BEFH$ là hình bình hành;
c) Từ $A$ kẻ $Ax$ song song $BC$ cắt $HF$ tại $D$. Chứng minh $ADCH$ là hình chữ nhật.
Hướng dẫn giải:
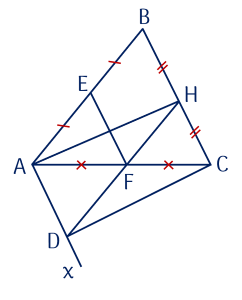
a) Xét tam giác $ABC$ có:
$E$, $F$ lần lượt là trung điểm của $AB$, $AC$
Nên $EF$ là đường trung bình của tam giác $ABC$.
Suy ra $EF$ // $BC$
Xét tứ giác $EFCB$ có: $EF$ // $BC$ và $\widehat{B}=\widehat{C}$ ($\triangle A B C$ cân tại A)
Nên $EFCB$ là hình thang cân
b) Ta có: $EF$ // $BC$ nên $EF$ // $BH$, ($H$ thuộc $BC$) (1)
Mặt khác $EF=\dfrac{BC}{2}$, ($EF$ là đường trung bình của tam giác $ABC$).
$B H=\dfrac{B C}{2}$, ($H$ là trung điểm $BC$)
Nên $F E=B H$ (2)
Từ (1) và (2) suy ra BEFH là hình bình hành.
c) Chứng minh $\triangle A F D=\triangle C F H$ (g.c.g)
Suy ra ${FD}={FH}$
Xét tứ giác $AHCD$ có ${EF}={FD}$ (cmt) và ${FC}={FA}$ (gt)
Nên ${AHCD}$ là hình bình hành.
Mà $\widehat{H}=90^{\circ}$ ($AH$ là đường trung tuyến đồng thời là đường cao của tam giác cân $ABC$).
Suy ra $AHCD$ là hình chữ nhật.
